← Zpět na rozcestník

✏️ Geometrické konstrukce — jak na rýsování

Kružítko, pravítko a trocha přemýšlení. Vždy hledej VŠECHNA řešení!

🔑 Jak na geometrické konstrukce?

  1. Nakresli si, co VÍŠ (dané body, přímky, vzdálenosti)
  2. Kružnice = všechny body ve stejné vzdálenosti od středu
  3. Kolmice a rovnoběžky pomocí trojúhelníku s pravítkem
  4. VŽDY hledej VŠECHNA řešení (u CERMATu typicky 2!)
Procvičuj příklady z přijímaček:
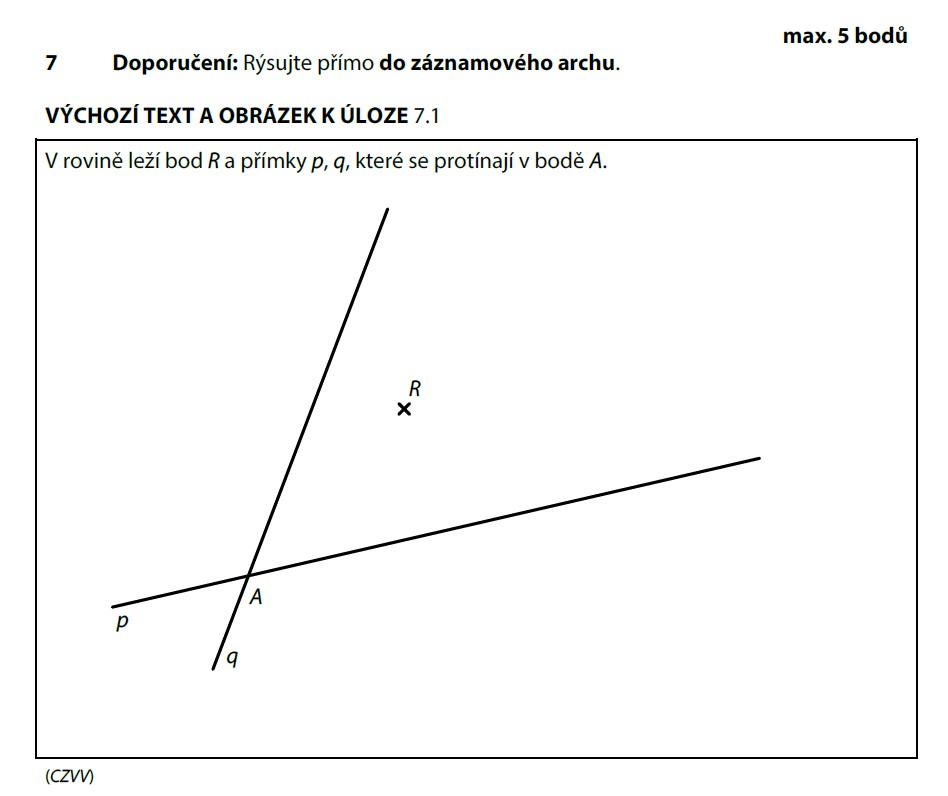
📋 Zadání — 1. řádný termín, Úloha 7 (5 bodů)
7.1) Obdélník ABCD
Bod A je dán, bod B leží na přímce p, bod C leží na přímce q. Bod R leží na straně BC. Sestrojte všechna řešení.
7.2) Trojúhelník EFG
Bod S je střed kružnice opsané. Strana EF leží na přímce m, strana EG leží na přímce n. Sestrojte trojúhelník.
Zadání
Zadání
Zadání
1 7.1: Obdélník ABCD — co víme?

U obdélníku platí: protější strany jsou rovnoběžné a všechny úhly jsou pravé (90°). To je náš hlavní nástroj!

Co máme dáno:

  1. Bod A — už máme narýsovaný
  2. Přímka p — na ní leží bod B
  3. Přímka q — na ní leží bod C
  4. Bod R — leží na straně BC

Strana AB musí být kolmá na stranu AD (pravý úhel v A).

2 7.1: Postup konstrukce

Rýsujeme krok za krokem:

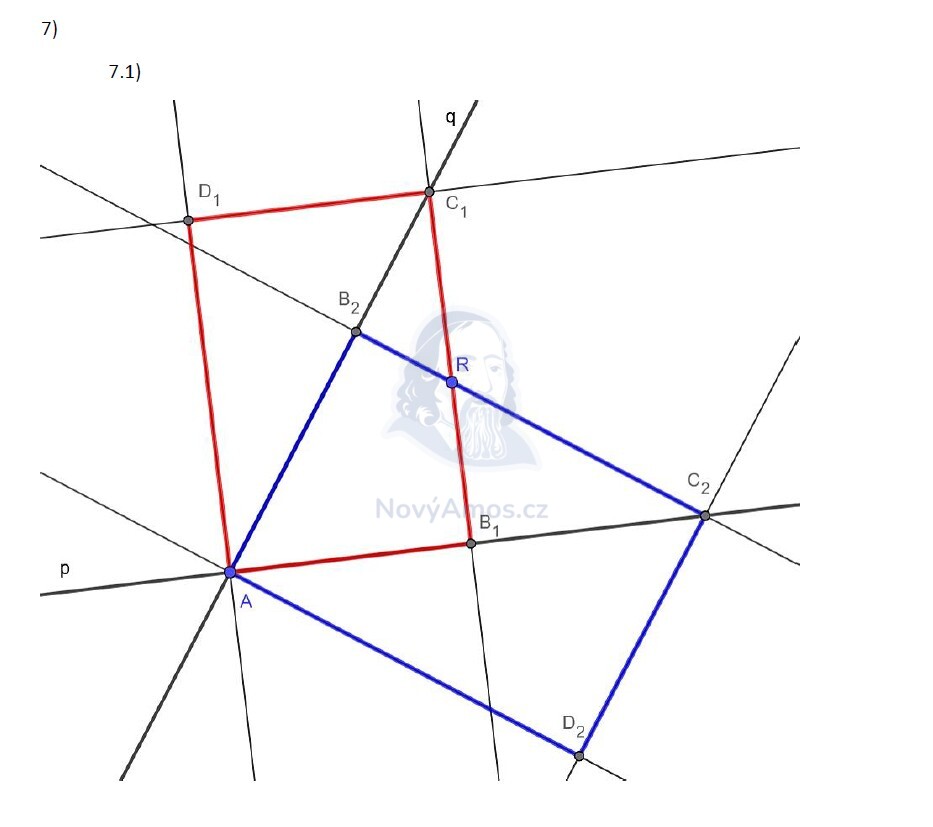
  1. Z bodu A vedeme kolmici k přímce p — na kolmici a přímce p najdeme bod B (průsečík)
  2. Z bodu B vedeme rovnoběžku s přímkou AD — ta prochází bodem R a pokračuje k přímce q
  3. Průsečík s přímkou q je bod C
  4. Bod D sestrojíme tak, aby AD bylo rovnoběžné s BC a kolmé na AB

Bod B může ležet na přímce p na dvou stranách od bodu A, proto existují 2 řešení!

3 7.2: Trojúhelník EFG — kružnice opsaná

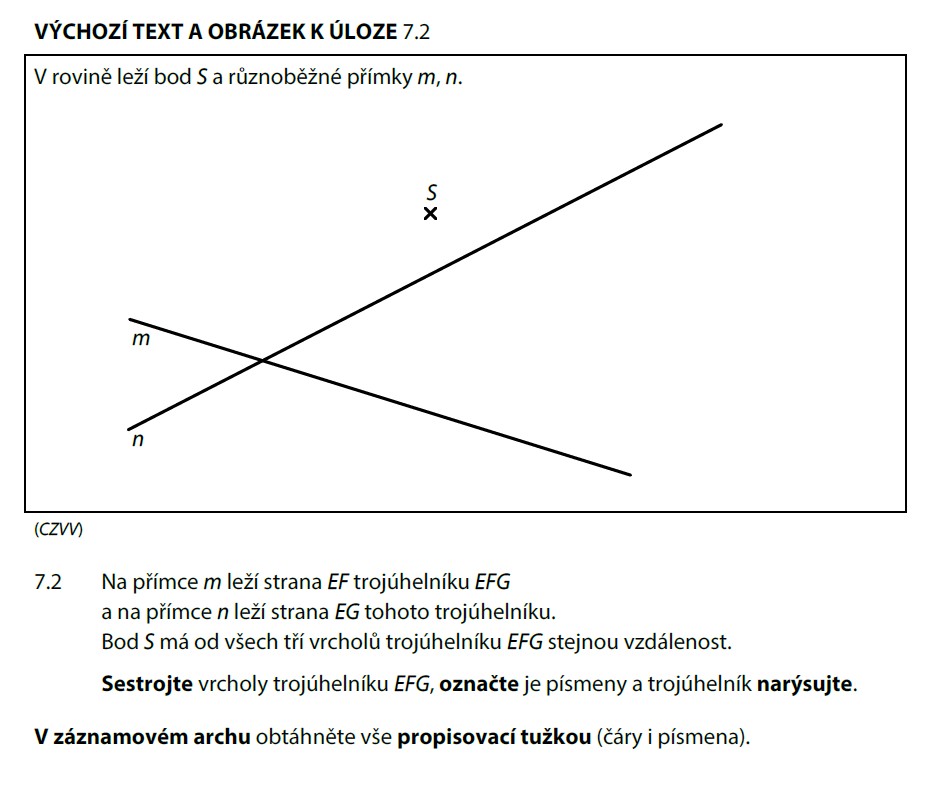
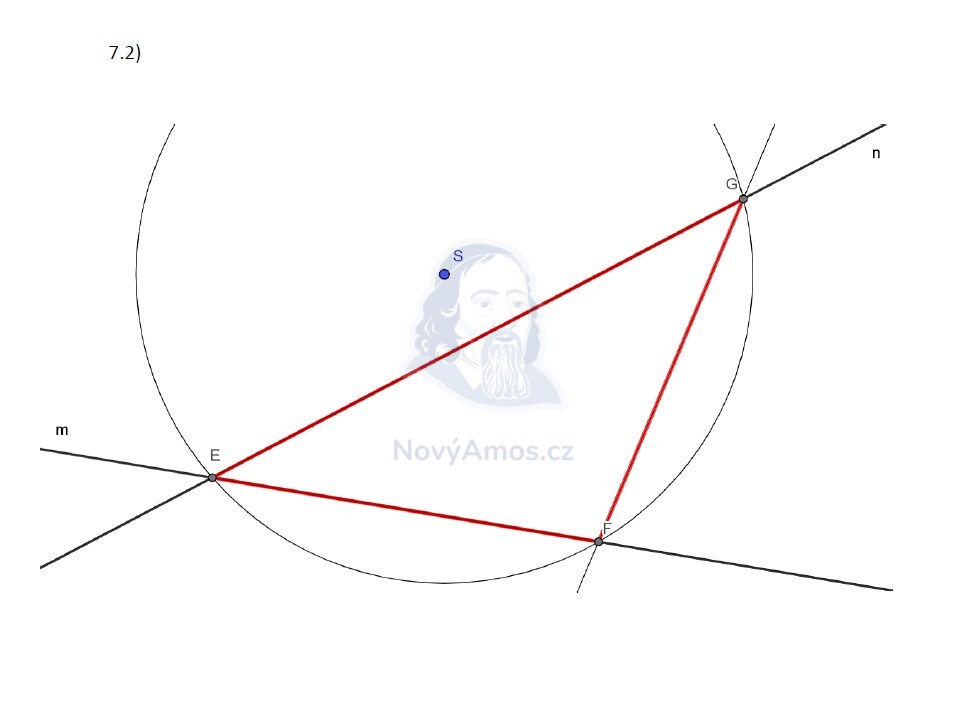
S je střed kružnice opsané = je stejně daleko od E, F i G. To znamená:

|SE| = |SF| = |SG| = r (poloměr kružnice)
  1. EF leží na přímce m → body E a F jsou průsečíky kružnice (střed S, poloměr r) s přímkou m
  2. EG leží na přímce n → bod G je průsečík kružnice s přímkou n
  3. Spojíme body E, F, G a máme trojúhelník

Počet řešení závisí na poloze přímek m a n vůči kružnici.

4 Tip k rýsování

Při konstrukci vždy zapiš POSTUP — CERMAT dává body za správný zápis, ne jen za obrázek!

  1. Napiš: „Sestrojím kolmici z bodu A k přímce p..."
  2. Napiš: „Sestrojím rovnoběžku s AB procházející bodem C..."
  3. Každý krok očísluj
  4. Na konci napiš: „Úloha má 2 řešení" (nebo kolik jich je)

I když se ti obrázek moc nepovede, za správný postup dostaneš body!

✅ Výsledek
7.1) 2 řešení    7.2) dle polohy přímek
💡 Tip pro CERMAT

U obdélníku si pamatuj tři klíčové vlastnosti:

  • Protější strany jsou rovnoběžné (AB ∥ CD, AD ∥ BC)
  • Všechny úhly jsou pravé (90°) — používej kolmice!
  • Úhlopříčky se půlí — střed jedné je i středem druhé
📝 Oficiální řešení CERMAT
Řešení Řešení
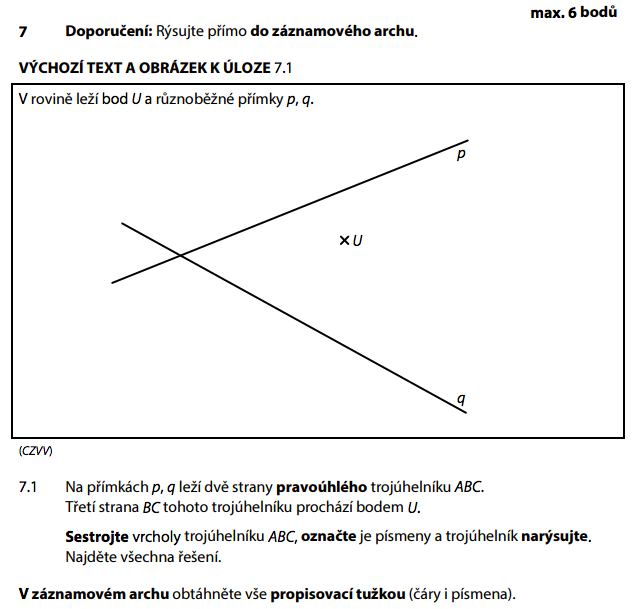
📋 Zadání — 2. řádný termín, Úloha 7 (6 bodů)
7.1) Pravoúhlý trojúhelník ABC
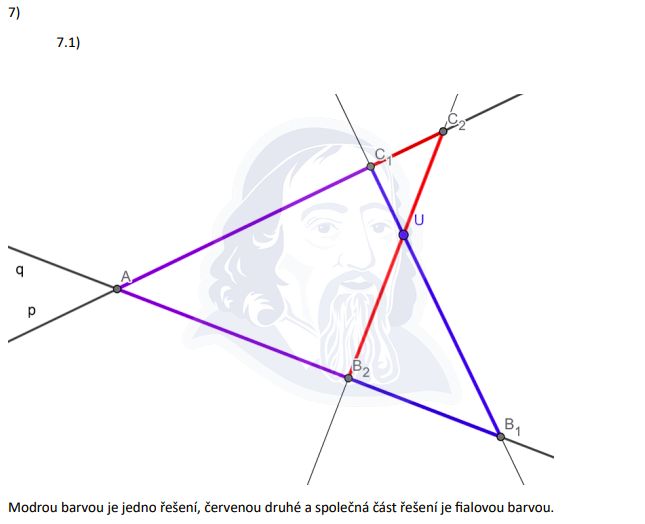
Dvě strany leží na přímkách p a q. Třetí strana BC prochází bodem U. Sestrojte všechna řešení. (2 řešení)
7.2) Obdélník KLMN
K je daný bod. KL je rovnoběžná s přímkou r. Na přímce s leží střed S strany KN a vrchol M. (1 řešení)
Zadání
Zadání
1 7.1: Pravoúhlý trojúhelník — kde je pravý úhel?

Dvě strany leží na přímkách p a q. Pokud se p a q protínají, jejich průsečík je vrchol A s pravým úhlem!

  1. Najdeme průsečík přímek p a q → to je vrchol A (pravý úhel)
  2. Bod B leží na jedné přímce (třeba p), bod C na druhé (q)
  3. Strana BC prochází bodem U
  4. Přímku BC vedeme bodem U — průsečíky s p a q dají body B a C
2 7.1: Proč jsou 2 řešení?

Bodem U můžeme vést přímku BC dvěma různými způsoby:

  1. 1. řešení: B leží na přímce p, C leží na přímce q
  2. 2. řešení: B leží na přímce q, C leží na přímce p (prohodíme je!)

Proto vznikají 2 řešení. CERMAT chce obě!

3 7.2: Obdélník KLMN — postup

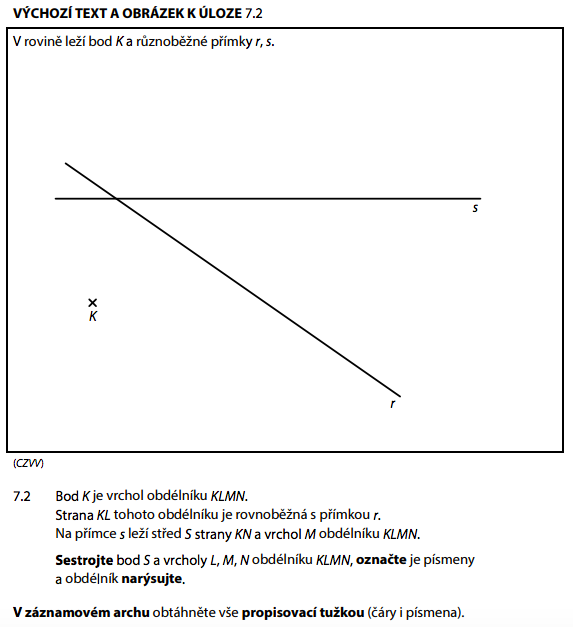
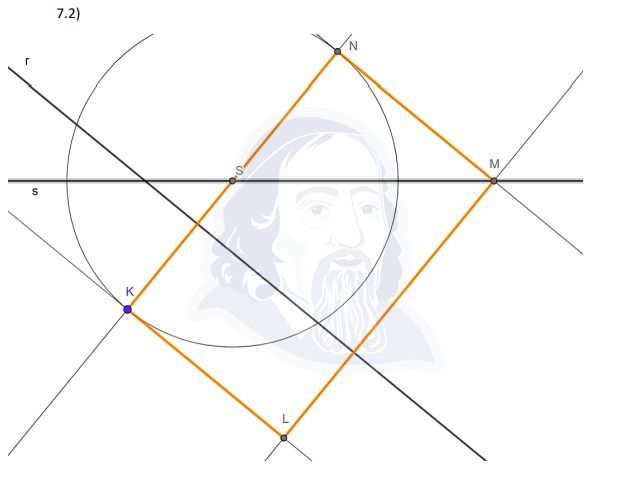
Co víme: K je dán, S je střed KN a leží na přímce s, M leží na přímce s.

  1. S je střed strany KN → narýsujeme kružnici se středem S procházející K
  2. Průsečík kružnice s přímkou s dá bod N (protože |SK| = |SN|)
  3. KL je rovnoběžná s přímkou r → z K vedeme rovnoběžku s r
  4. M leží na přímce s a KLMN je obdélník → M najdeme jako průsečík
  5. L doplníme tak, aby KLMN byl obdélník

Vychází 1 řešení.

4 Kontrola — ověř si výsledek!

Po narýsování si vždy zkontroluj:

  1. Jsou protější strany rovnoběžné? (u obdélníku i pravoúhlého trojúhelníku)
  2. Leží body na správných přímkách? (B na p, C na q...)
  3. Jsou úhly opravdu pravé? (změř trojúhelníkem)
  4. Prochází strana BC bodem U?

Kontrola trvá minutu, ale může ti zachránit body!

✅ Výsledek
7.1) 2 řešení    7.2) 1 řešení
💡 Tip pro CERMAT

Střed strany = bod, odkud je stejná vzdálenost k oběma koncům. Když znáš střed S a jeden konec K:

  • Narýsuješ kružnici se středem S a poloměrem |SK|
  • Druhý konec N leží na kružnici (na opačné straně od K)
  • Tohle je klíčový trik pro spoustu úloh!
📝 Oficiální řešení CERMAT
Řešení Řešení
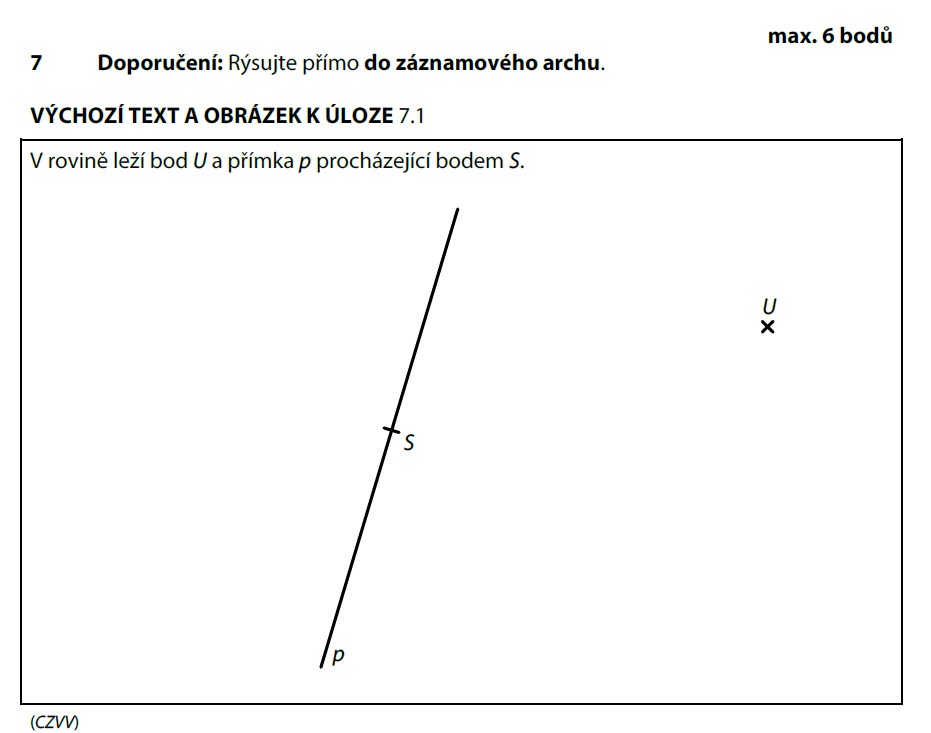
📋 Zadání — 1. náhradní termín, Úloha 7 (6+6 bodů)
7.1) Pravoúhlý trojúhelník ABC s pravým úhlem při A
Strana AB leží na přímce p procházející bodem S. S je střed AB, |AS| = 3 cm. Vrchol C leží na polopřímce US.
7.2) Obdélník KLMN
K je daný bod, M leží na přímce m. |MR| = |KR|, kde bod R leží na přímce m.
Zadání
Zadání
Zadání
1 7.1: Najdeme body A a B

S je střed AB a |AS| = 3 cm. To znamená, že A i B jsou od S stejně daleko — přesně 3 cm.

  1. Narýsujeme kružnici se středem S a poloměrem 3 cm
  2. Průsečíky kružnice s přímkou p jsou body A a B
  3. Dostaneme dva body — ale pozor: A a B se mohou prohodit!
|AS| = |BS| = 3 cm  →  |AB| = 6 cm
2 7.1: Najdeme bod C

Pravý úhel je při A, takže z bodu A vedeme kolmici k přímce p:

  1. Z bodu A sestrojíme kolmici k přímce p
  2. Bod C leží na polopřímce US a zároveň na kolmici z A
  3. Průsečík kolmice a polopřímky US je bod C

Protože A a B se mohou prohodit (jeden je vlevo, druhý vpravo od S), vznikají 2 řešení.

3 7.2: Obdélník KLMN — využijeme kružnici

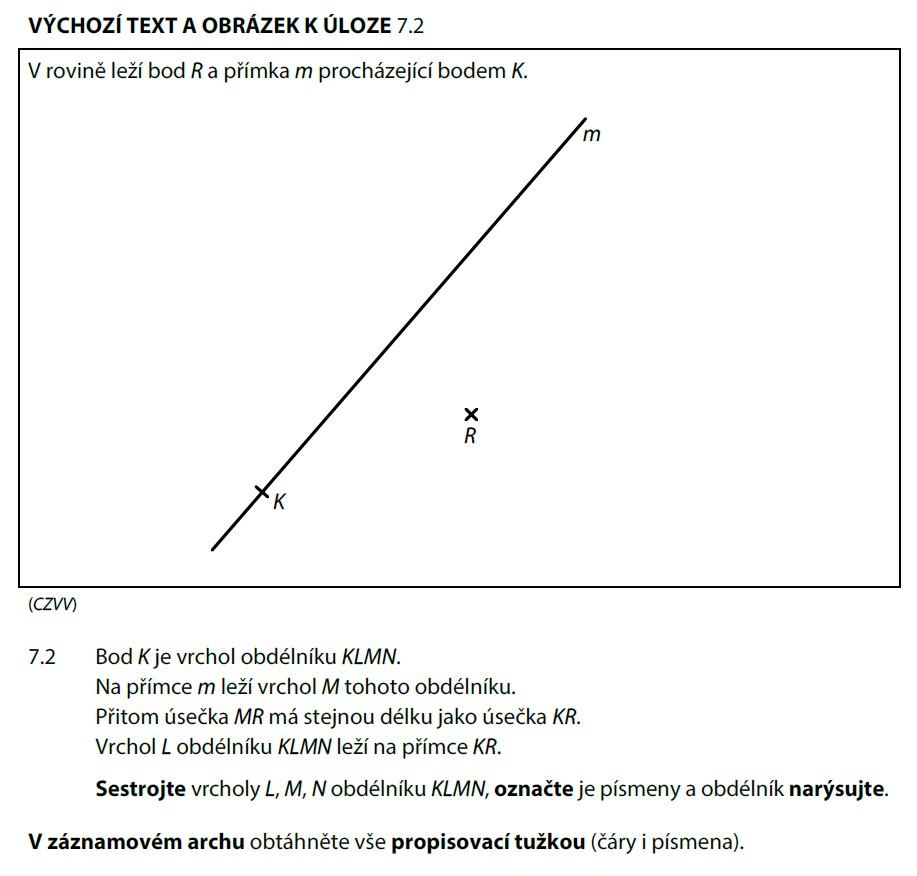
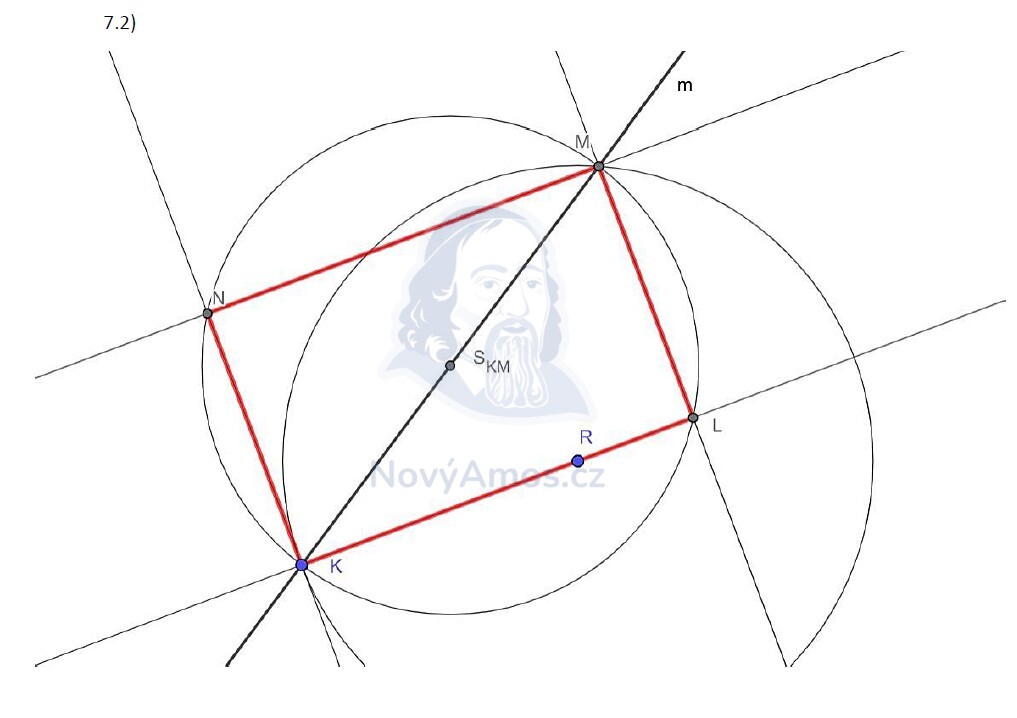
|MR| = |KR| znamená, že M je od R stejně daleko jako K. To je práce pro kružnici!

  1. Spočítáme vzdálenost |KR| (změříme kružítkem)
  2. Narýsujeme kružnici se středem R a poloměrem |KR|
  3. Průsečík kružnice s přímkou m je bod M
  4. Zbývající vrcholy L a N doplníme pomocí rovnoběžek a kolmic (obdélník!)

Vychází 1 řešení.

✅ Výsledek
7.1) 2 řešení    7.2) 1 řešení
💡 Tip pro CERMAT

Kdykoli v zadání vidíš „střed úsečky" nebo „stejná vzdálenost", mysli na kružnici!

  • Střed AB, vzdálenost 3 cm → kružnice se středem S, poloměr 3 cm
  • |MR| = |KR| → kružnice se středem R, poloměr |KR|
  • Kružnice je tvůj nejlepší kamarád u konstrukčních úloh!
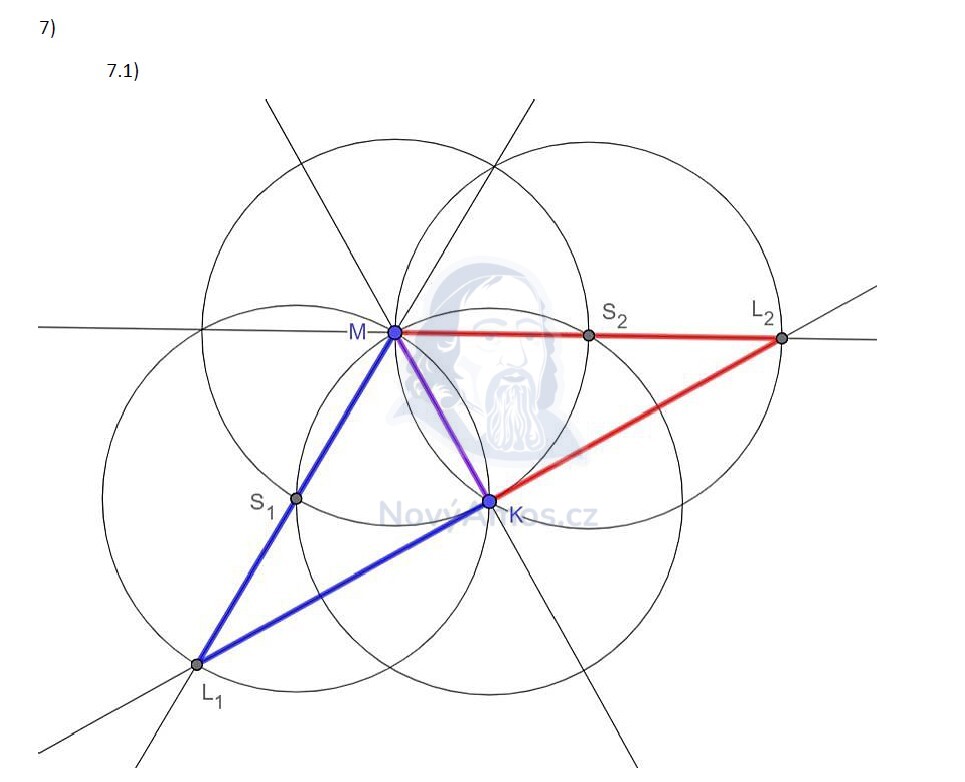
📝 Oficiální řešení CERMAT
Řešení
📋 Zadání — 2. náhradní termín, Úloha 7 (6+6 bodů)
7.1) Trojúhelník KLM
Body K a M jsou dány. S je střed LM. Trojúhelník KMS je rovnostranný. Sestrojte bod S a bod L. Určete počet řešení.
7.2) Čtverec ABCD
Bod A je dán, bod B leží na přímce p. Bod R je stejně daleko od A i B. Bod R neleží uvnitř čtverce.
Zadání
Zadání
1 7.1: Rovnostranný trojúhelník KMS

Rovnostranný trojúhelník má všechny strany stejně dlouhé:

|KM| = |KS| = |MS|

Známe K a M, takže známe vzdálenost |KM|. Bod S musí být od K i M stejně daleko jako |KM|.

  1. Narýsujeme kružnici se středem K a poloměrem |KM|
  2. Narýsujeme kružnici se středem M a poloměrem |KM|
  3. Průsečíky obou kružnic jsou dva body S (jeden „nahoře", druhý „dole")

Kružnice se vždy protnou ve dvou bodech → 2 body S!

2 7.1: Najdeme bod L

S je střed LM. To znamená, že L a M jsou od S stejně daleko, ale na opačných stranách.

  1. S je střed → L leží na přímce SM, na opačné straně od M
  2. Vzdálenost |SL| = |SM| (S je přesně uprostřed)
  3. Bod L najdeme tak, že od S naměříme vzdálenost |SM| na druhou stranu

Pro každý bod S dostaneme jeden bod L → celkem 2 řešení.

3 7.2: Čtverec ABCD — osa úsečky

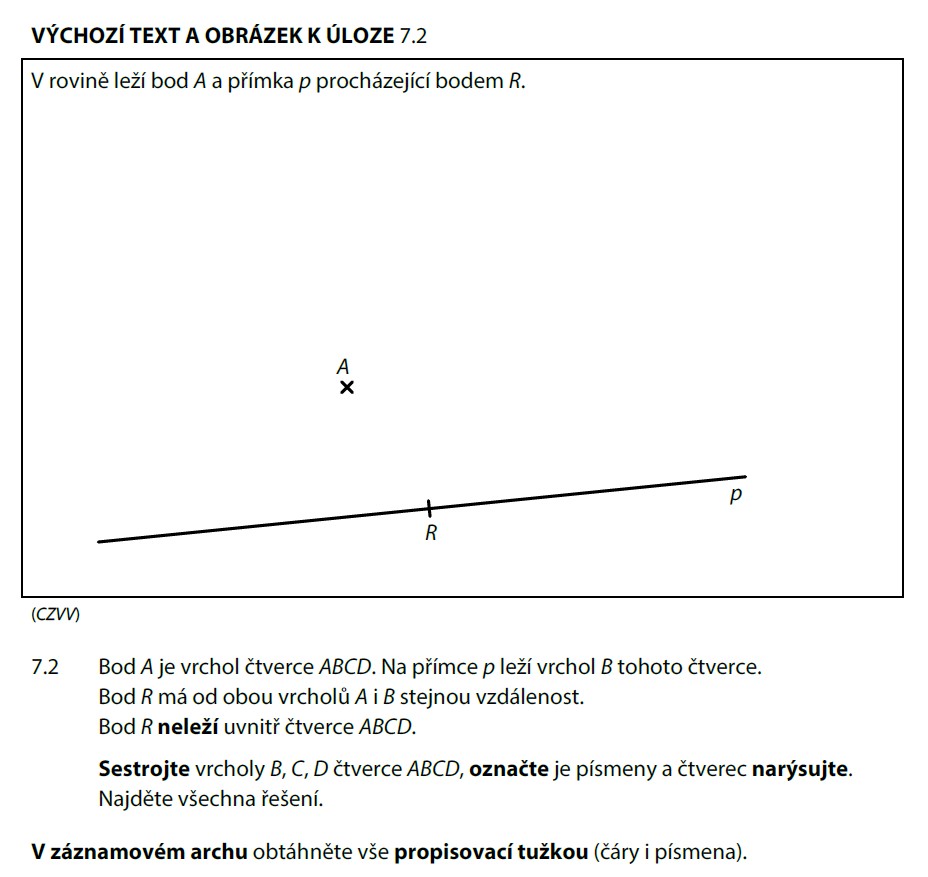
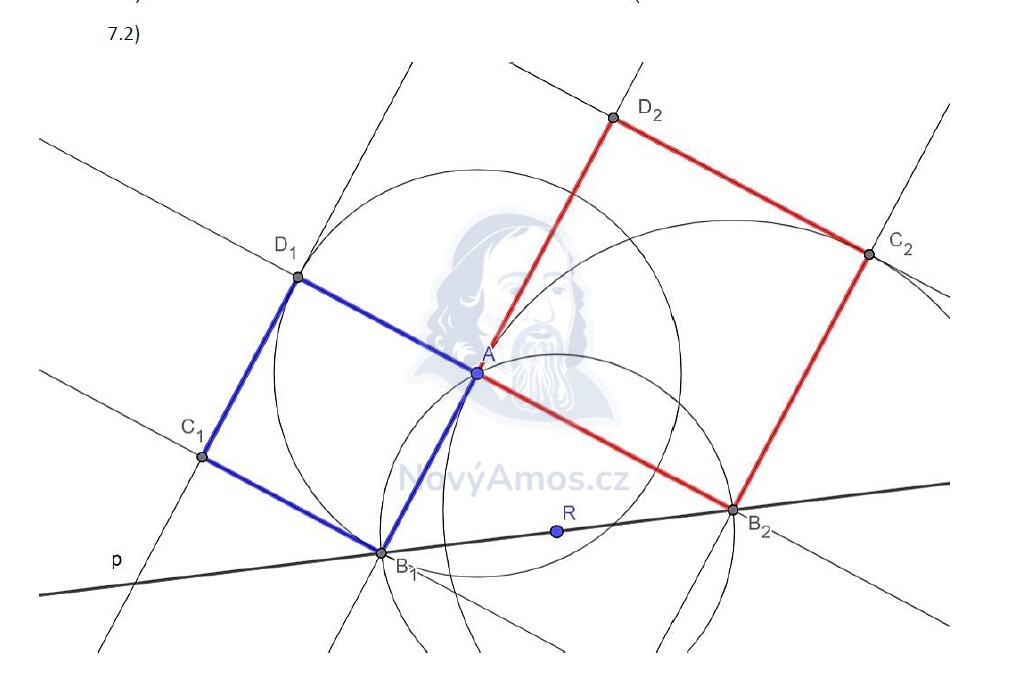
R je stejně daleko od A i B. Všechny takové body leží na ose úsečky AB (kolmice v polovině AB).

  1. A je dán, B leží na přímce p
  2. ABCD je čtverec → |AB| je délka strany, tu zatím neznáme
  3. Osa AB prochází bodem R a je kolmá na AB
  4. B najdeme jako průsečík přímky p s přímkou AB (kde AB je kolmá na osu procházející R)
  5. R neleží uvnitř čtverce — to nám pomůže vybrat správné řešení

Přímka p může dát 2 průsečíky → 2 řešení.

4 Zápis konstrukce — jak získat plné body

U každé konstrukce CERMAT chce kompletní zápis. Takhle to má vypadat:

  1. Dáno: body K, M (nebo co je v zadání)
  2. Postup:
    1. Sestrojím kružnici k₁(K; |KM|)
    2. Sestrojím kružnici k₂(M; |KM|)
    3. Průsečíky k₁ a k₂ jsou body S₁ a S₂
    4. Pro každý S sestrojím bod L...
  3. Závěr: Úloha má 2 řešení.

Za takový zápis dostaneš plný počet bodů!

✅ Výsledek
7.1) 2 řešení    7.2) 2 řešení
⚠️ Pozor — důležité pro CERMAT!

Konstrukce je VŽDY úloha 7 a má NEJVÍC bodů (5-6 bodů)! Vyplatí se jí věnovat čas.

  • Vždy hledej všechna řešení — typicky existují 2
  • Zapiš celý postup (dáno → postup → závěr)
  • I nepřesný obrázek se správným postupem = body!
  • Nezapomeň na závěr: „Úloha má X řešení"
📝 Oficiální řešení CERMAT
Řešení Řešení

🎯 Rady pro CERMAT: Geometrické konstrukce

Co si odnést z tohoto tématu

🧭 Strategie řešení
  • Nakresli si, co VÍŠ (dané body, přímky, vzdálenosti) — pak hledej průsečíky
  • Kružnice = všechny body ve stejné vzdálenosti. Střed úsečky? Stejná vzdálenost? Vždy mysli na kružnici!
  • U obdélníku: protější strany rovnoběžné, úhly pravé, úhlopříčky se půlí
  • Vždy hledej VŠECHNA řešení — u CERMATu typicky existují 2!
⚠️ Typické chytáky
  • Konstrukce je VŽDY úloha 7 a má NEJVÍC bodů (5-6) — vyplatí se jí věnovat čas!
  • Za správný zápis postupu dostaneš body i s nepřesným obrázkem
  • Nezapomeň na závěr: „Úloha má X řešení" — bez něj přijdeš o body
  • Dva průsečíky kružnice s přímkou = dva možné body = dvě řešení
❌ Nejčastější chyby
  • Najít jen jedno řešení a zapomenout na druhé (prohozené body)
  • Nezapsat postup — CERMAT dává body za zápis, ne jen za obrázek
  • Zapomenout ověřit, že body leží na správných přímkách a úhly jsou opravdu pravé
  • Nepoužít strukturu: Dáno → Postup → Závěr