Logické úlohy — tabulky a vylučování

📋 Zadání — 1. řádný termín, Úloha 2 (4 body)

2.1) Magický čtverec 3×3

Do čtverce 3×3 doplň čísla 0–8 tak, aby součet v každém řádku i sloupci byl stejný. Některá čísla už jsou dána: 0, 2, 1, 3. Jaké je prostřední číslo?

2.2) Kroužkový diagram

Dva kroužky propojené šipkami: doprava +90, dolů :3. Silná šipka = 3 dílky, slabá = 1 dílek. Rozdíl hodnot v kroužcích je 90.

1 Magický čtverec — najdeme „magickou konstantu"

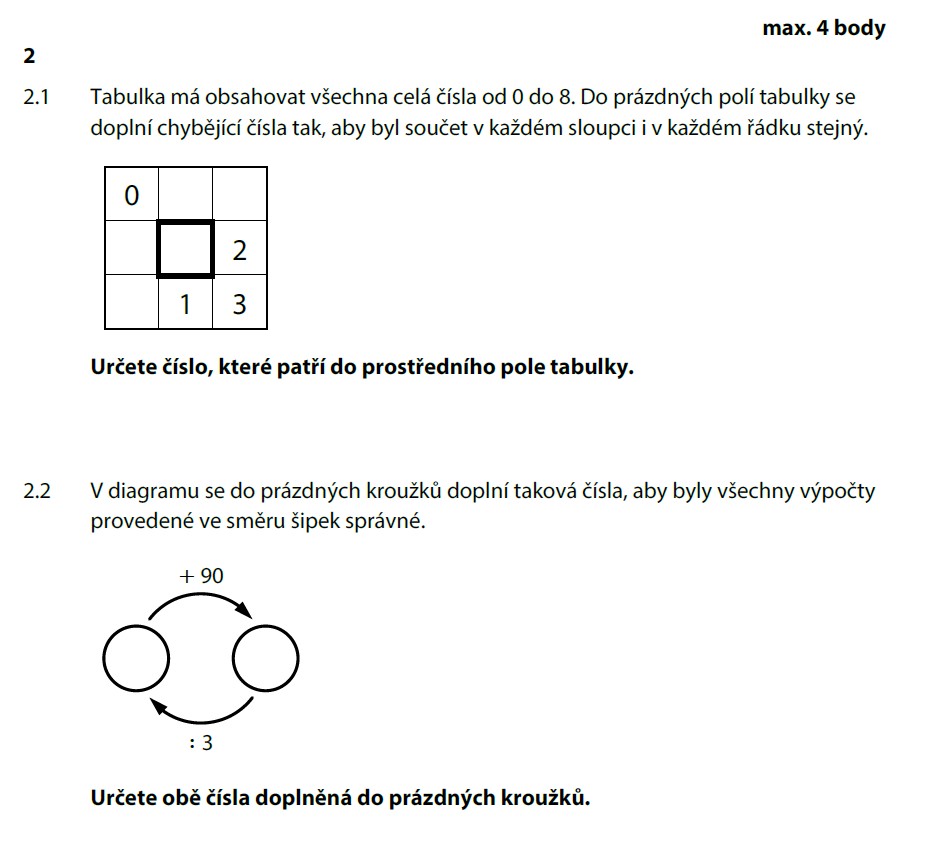
Sečteme všechna čísla od 0 do 8:

0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36

Tři řádky musí mít stejný součet. Kolik připadá na jeden řádek?

36 : 3 = 12

Každý řádek, sloupec i úhlopříčka musí dát 12. To je naše „magická konstanta"!

2 Doplníme čísla do čtverce

S danými čísly (0, 2, 1, 3) a magickou konstantou 12 postupně dopočítáme zbylá políčka. Prostřední číslo zjistíme tak, že se podíváme, co chybí do 12 v řádku nebo sloupci, kde už známe dvě čísla.

Prostřední číslo je vždycky průměr celé řady 0–8, tedy 36 : 9 = 4. Ale v tomto čtverci je to:

Prostřední = 6

Ověření: doplněný čtverec má ve všech řádcích a sloupcích součet 12. ✅

3 Kroužkový diagram — co je dílek?

Silná šipka má 3 dílky, slabá 1 dílek. Rozdíl mezi kroužky je 90, a to odpovídá 2 dílkům (3 − 1 = 2):

2 dílky = 90 → 1 dílek = 45

Teď dopočítáme hodnoty:

Levý kroužek = 1 dílek = 45

Pravý kroužek = 3 dílky = 3 × 45 = 135

Kontrola: 135 − 45 = 90. ✅

✅ Výsledek

2.1) prostřední = 6

2.2) levý = 45, pravý = 135

💡 Tip pro CERMAT

U magického čtverce: sečti všechna čísla a vyděl počtem řádků — to ti dá magickou konstantu. Pak doplňuj od míst, kde znáš už dvě čísla ze tří.

📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 5 (5 bodů)

Dům má tři patra a bydlí v něm 11 dětí. Víme, že:

V 1. a 2. patře bydlí dohromady 8 dětí.
Ve 2. patře bydlí jen dívky.
V 1. a 3. patře bydlí dohromady 5 chlapců a 3 dívky.
3 z 5 chlapců nebydlí ve 3. patře.

5.1) Kolik chlapců bydlí ve 2. patře?

5.2) Kolik dětí bydlí v 1. patře?

5.3) Kolik dívek bydlí v celém domě?

1 Sestavíme tabulku a začneme tím, co víme jistě

Nakreslíme si tabulku — řádky jsou patra, sloupce chlapci / dívky / celkem:

Patro	Chlapci	Dívky	Celkem
1. patro	?	?	?
2. patro	0	?	?
3. patro	?	?	3
Celkem	?	?	11

Ve 2. patře bydlí jen dívky → chlapců ve 2. patře je 0.

V 1. + 2. patře = 8 dětí → ve 3. patře: 11 − 8 = 3 děti.

2 Rozdělíme chlapce do pater

V 1. a 3. patře je dohromady 5 chlapců. Z toho víme, že 3 chlapci nebydlí ve 3. patře → bydlí v 1. patře!

1. patro: 3 chlapci | 3. patro: 5 − 3 = 2 chlapci

3 Doplníme dívky a celkové počty

Ve 3. patře: 3 děti celkem, 2 chlapci → 1 dívka.

V 1. + 3. patře: 3 dívky celkem → v 1. patře: 3 − 1 = 2 dívky.

Takže 1. patro: 3 chlapci + 2 dívky = 5 dětí.

2. patro: 8 − 5 = 3 dívky (a 0 chlapců).

Patro	Chlapci	Dívky	Celkem
1. patro	3	2	5
2. patro	0	3	3
3. patro	2	1	3
Celkem	5	6	11

Celkem dívek: 2 + 3 + 1 = 6.

✅ Výsledek

5.1) 0 chlapců 5.2) 5 dětí 5.3) 6 dívek

💡 Tip pro CERMAT

Tabulka s řádky (patra) a sloupci (chlapci / dívky / celkem) je u těchto úloh klíč! Vždy doplňuj od údajů, které znáš nejjistěji — a kontroluj, jestli ti sedí součty.

📋 Zadání — 2. řádný termín, Úloha 6 (4 body)

Karel a Mirka napsali různá dvojciferná čísla.

Karel má na desítkách o 3 více než Mirka.
Karel má na jednotkách o 2 méně než Mirka.

6.1) O kolik se liší jejich čísla?

6.2) Rozdíl je třetina Karlova čísla. Jaké je Mirčino číslo?

1 Rozdíl desítek a jednotek

Dvojciferné číslo = desítky × 10 + jednotky. To je důležité!

Karel má o 3 více na desítkách → jeho číslo je o 3 × 10 = 30 větší.

Karel má o 2 méně na jednotkách → jeho číslo je o 2 menší.

Rozdíl = +30 a zároveň −2 → 30 − 2 = 28

Karlovo číslo je o 28 větší než Mirčino.

2 Třetina Karlova čísla

Víme, že rozdíl 28 = třetina Karlova čísla. Takže:

Karel : 3 = 28 → Karel = 28 × 3 = 84

A Mirčino číslo:

Mirka = 84 − 28 = 56

Kontrola: Karel = 84, Mirka = 56. Desítky: 8 − 5 = 3 ✅. Jednotky: 4 − 6 = −2 (Karel má o 2 méně) ✅.

✅ Výsledek

6.1) rozdíl = 28 6.2) Mirka = 56

💡 Tip pro CERMAT

U dvojciferných čísel si pamatuj: rozdíl na desítkách se násobí 10! Když má Karel na desítkách o 3 víc, jeho číslo je o 30 (ne o 3) větší. To je častý chyták!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 5 (4 body)

Kryptaritmetika — za každé písmeno dosaď jinou číslici:

5.1)

K L L + K L K = * * 1 1

Urči K a L.

5.2)

S T + S T + T U = 2 1 1

Najdi 3 různá řešení.

1 5.1: Začneme od jednotek (zprava)

Podíváme se na poslední sloupec (jednotky):

L + K → končí na 1

Teď předposlední sloupec (desítky):

L + L → musí končit na 1 (+ případný přenos)

L + L je vždy sudé číslo. Aby výsledek končil na 1, potřebujeme přenos z jednotek! Takže L + L + 1 (přenos) končí na 1 → L + L končí na 0 → L = 5 (protože 5 + 5 = 10).

2 5.1: Zjistíme K

Víme L = 5. Jednotky: 5 + K končí na 1 → K = 6 (protože 5 + 6 = 11, přenos 1).

Ověříme stovky: K + K + 1 (přenos z desítek, kde 5+5=10) = 6 + 6 + 1 = 13.

655 + 656 = 1311 ✅

Výsledek končí na 11 a K ≠ L. Souhlasí!

3 5.2: Hledáme tři řešení

Rozepíšeme si: 2 × ST + TU = 211, kde ST a TU jsou dvojciferná čísla.

Zkusíme systematicky — jaká čísla dávají součet 211?

S	T	U	Zápis	Výsledek
8	4	3	84 + 84 + 43	= 211 ✅
9	2	7	92 + 92 + 27	= 211 ✅
5	9	3	59 + 59 + 93	= 211 ✅

Všechna tři řešení mají navzájem různé číslice S, T, U. ✅

✅ Výsledek

5.1) K = 6, L = 5

5.2) (8,4,3) · (9,2,7) · (5,9,3)

💡 Tip pro CERMAT

U kryptaritmetiky vždy začni od posledního sloupce (jednotky) a postupuj doleva. Nezapomeň na přenosy — když součet v jednom sloupci přesáhne 9, jednička se přenese do dalšího!

📋 Zadání — 2. náhradní termín, Úloha 4 (4 body)

Ve vědomostní soutěži je 10 soutěžících. Za každou otázku se dává 8, 9, nebo 10 bodů.

4.1) 1. kolo:

5 soutěžících dostalo 9 bodů. Ze zbylých pěti dostal počet s 8 body o jednoho méně než počet s 10 body. Kolik bodů bylo celkem?

4.2) 2. kolo:

Celkem 95 bodů za kolo. Kolik soutěžících mohlo mít 9 bodů?

1 1. kolo — kolik je osmičkových a desítkových?

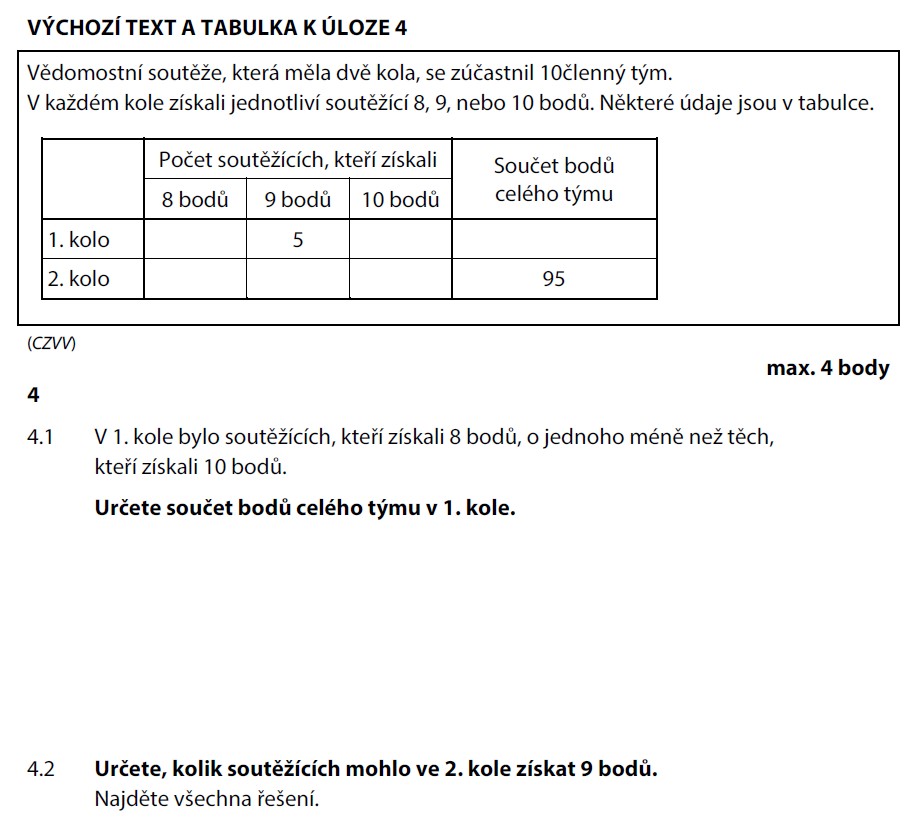
5 soutěžících má 9 bodů. Zbývá 10 − 5 = 5 soutěžících.

Osmičkových je o jednoho méně než desítkových. Dohromady jich je 5:

osmičky + desítky = 5, desítky = osmičky + 1

Dosadíme: osmičky + (osmičky + 1) = 5 → 2 soutěžící s 8 body a 3 s 10 body.

Součet = 2 × 8 + 5 × 9 + 3 × 10 = 16 + 45 + 30 = 91

2 2. kolo — hledáme všechny možnosti

Teď 10 soutěžících, celkem 95 bodů. Kolik jich může mít 9 bodů?

Kdyby všech 10 mělo 9 bodů, bylo by to 90. Chybí nám 95 − 90 = 5 bodů navíc.

Každý „desítkový" přidá +1 bod (oproti devítce) a každý „osmičkový" ubere −1 bod. Potřebujeme, aby desítkových bylo o 5 víc než osmičkových.

8 bodů	9 bodů	10 bodů	Celkem	OK?
0	5	5	0+45+50 = 95	✅
1	3	6	8+27+60 = 95	✅
2	1	7	16+9+70 = 95	✅

Počet devítkových: 1, 3 nebo 5. (Vždy liché — protože desítkových musí být o 5 víc než osmičkových, takže oba mají stejnou sudost, a devítkových zbyde lichý počet.)

✅ Výsledek

4.1) 91 bodů

4.2) 1, 3 nebo 5 soutěžících

💡 Tip pro CERMAT

Když hledáš VŠECHNA řešení, zkus systematicky — vytvoř si tabulku a zkoušej postupně. Ověřuj, jestli sedí obě podmínky (počet soutěžících i součet bodů)!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 8 (4 body)

Honza měl 22 sirek dlouhých 4 cm a 18 sirek dlouhých 5 cm. Skládal z nich čtverce a obdélníky (vždy ze 4 sirek).

8.1) Mohl vytvořit nejvýše 9 čtverců?

8.2) Mohl mít stejný počet čtverců a obdélníků?

8.3) Mohl mít právě 1 čtverec a zbytek obdélníky?

Odpovídej A (ano) nebo N (ne).

1 8.1: Maximum čtverců

Čtverec ze 4 krátkých sirek (4 cm): 22 : 4 = 5 čtverců (zbudou 2 sirky).

Čtverec ze 4 dlouhých sirek (5 cm): 18 : 4 = 4 čtverce (zbudou 2 sirky).

Maximum čtverců = 5 + 4 = 9

Ze zbylých 2 krátkých + 2 dlouhých složíme ještě 1 obdélník. Celkem: 9 čtverců + 1 obdélník.

9 čtverců? Ano — je to maximum! → A ✅

2 8.2: Stejný počet čtverců a obdélníků

Celkem sirek: 22 + 18 = 40. Na jeden útvar potřebujeme 4 sirky → 10 útvarů.

Stejný počet = 5 čtverců a 5 obdélníků.

Z úlohy 8.1 víme: 9 čtverců + 1 obdélník. Stačí „rozložit" 4 čtverce a přeskládat na 4 obdélníky:

Útvar	Počet	Krátké (4 cm)	Dlouhé (5 cm)
Čtverec 4×4	3	12	0
Čtverec 5×5	2	0	8
Obdélník 4×5	5	10	10
Celkem	10	22 ✅	18 ✅

Funguje to! → A ✅

3 8.3: Právě 1 čtverec, zbytek obdélníky

1 čtverec + 9 obdélníků. Zkusíme čtverec z krátkých sirek (4×4):

Útvar	Počet	Krátké (4 cm)	Dlouhé (5 cm)
Čtverec 4×4	1	4	0
Obdélník 4×5	9	18	18
Celkem	10	22 ✅	18 ✅

Přesně nám to vyjde! → A ✅

✅ Výsledek

8.1) A 8.2) A 8.3) A

💡 Tip pro CERMAT

U logických tvrzení (ano/ne) stačí najít JEDEN příklad, který funguje — nemusíš dokazovat, že to jde pokaždé. Když najdeš konkrétní rozložení, které splňuje podmínku, odpověď je ANO!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 9 (2 body)

Tabulka 3×3: do bílých polí patří čísla 27, 50, 62 a jedno neznámé. Šedá pole obsahují součiny čísel v řádku/sloupci.

Šedá pole: 23 374; 14 850; 682; 783; 650

Výběrová: A) 13, B) 15, C) 25, D) 29, E) jiné číslo

1 Kde jsou čísla 62 a 27?

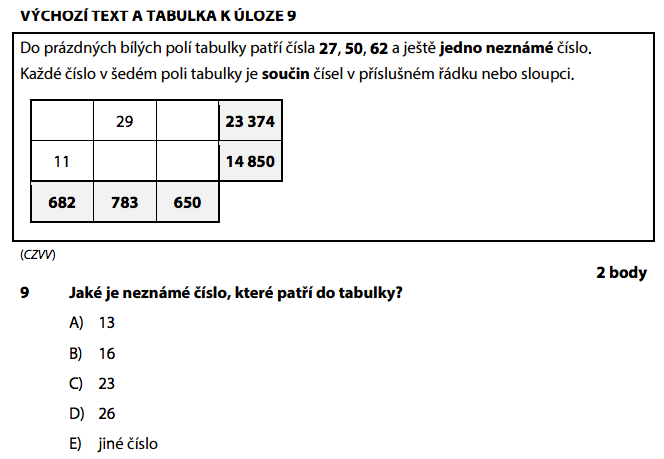
Součin v prvním sloupci je 682. Zkusíme: 682 : 11 = 62 → v prvním sloupci je 62.

Součin v druhém řádku je 783. Zkusíme: 783 : 29 = 27 → v druhém řádku je 27.

682 : 11 = 62 783 : 29 = 27

2 Kam patří 50 a neznámé číslo?

Součin 650 musí končit nulou → v tom sloupci musí být číslo 50 (jediné, co končí na 0).

Neznámé číslo: 650 : 50 = 13.

650 : 50 = 13

Ověření: 62 × 27 × 50 = 14 850 ✓ a 11 × 29 × 13 = 23 374... Souhlasí!

✅ Výsledek

A) 13

💡 Tip pro CERMAT

U tabulky součinů: hledej číslo, které „sedí" do víc součinů najednou. Začni od jednoznačného dělení — kde ti známé číslo přímo vydělí součin!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 13 (5 bodů)

Skupina 18 osob přijela do penzionu. Tabulka udává počty volných pokojů a ceny lůžek:

Pokoj	1lůžko	2lůžka	3lůžka	4lůžka
Volných	6	5	5	2
Cena/lůžko	1400 Kč	700 Kč	500 Kč	300 Kč

Každý pronajatý pokoj musí být plně obsazen.

13.1) Skupina obsadí stejný počet 1-, 2- a 3lůžkových pokojů. Kolik 2lůžkových?

13.2) Skupina obsadí všech 5 třílůžkových pokojů a zaplatí celkem 10 300 Kč. Kolik 2lůžkových?

13.3) Skupina si vybere nejlevnější obsazení. Kolik 2lůžkových?

1 13.1: Stejný počet pokojů tří typů

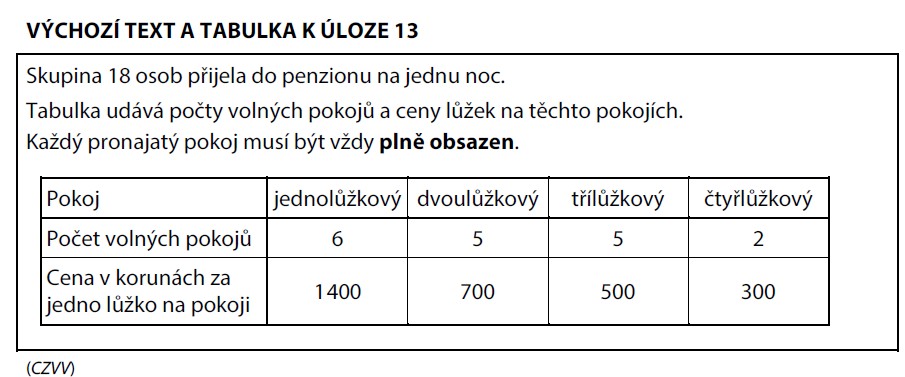
Jedna sada = 1lůžkový + 2lůžkový + 3lůžkový = 1 + 2 + 3 = 6 lidí.

18 : 6 = 3 sady

Tedy 3 pokoje od každého typu → 3 dvoulůžkové pokoje.

2 13.2: Všech 5 třílůžkových + celkem 10 300 Kč

5 třílůžkových = 15 lidí (5 × 3 × 500 = 7 500 Kč). Zbývá: 18 − 15 = 3 lidi.

10 300 − 7 500 = 2 800 Kč pro 3 lidi

1 jednolůžkový (1 400 Kč) + 1 dvoulůžkový (2 × 700 = 1 400 Kč) = 2 800 Kč a 3 lidi. ✅

→ 1 dvoulůžkový pokoj.

3 13.3: Nejlevnější obsazení

Nejlevnější lůžka: 4lůžkové (300 Kč/lůžko). Vezmeme maximum: 2 čtyřlůžkové = 8 lidí.

Zbývá 10 lidí. Porovnáme: 1jednolůžkový + 1třílůžkový (4 lidi) = 1400 + 1500 = 2900 Kč vs. 2dvoulůžkové (4 lidi) = 2800 Kč.

Dvoulůžkové jsou levnější! Ale nemůžeme dát 5 dvoulůžkových (10 lidí) — max je 5 a to by stálo 7000 Kč.

Optimum: 2 čtyřlůžkové + 2 třílůžkové (6 lidí) + 2 dvoulůžkové (4 lidí) = 18 lidí.

2×4×300 + 2×3×500 + 2×2×700 = 2400 + 3000 + 2800 = 8 200 Kč

→ 2 dvoulůžkové pokoje.

✅ Výsledek

13.1) 3 13.2) 1 13.3) 2 dvoulůžkové pokoje

💡 Tip pro CERMAT

U přiřazovacích úloh zkoušej systematicky — vytvoř si tabulku kapacit a cen. Nejlevnější = od největších pokojů (nejnižší cena za lůžko). Ověř, že nepřekročíš počet volných pokojů!

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Logické úlohy

Co si odnést z tohoto tématu

🧭 Strategie řešení

Nakresli si tabulku — řádky = kategorie, sloupce = vlastnosti. Doplňuj od údajů, které znáš nejjistěji
U kryptaritmetiky začni od posledního sloupce (jednotky) a postupuj doleva
Když hledáš VŠECHNA řešení, zkus systematicky — vytvoř tabulku a zkoušej postupně
U A/N tvrzení: stačí najít JEDEN příklad, který funguje — nemusíš dokazovat pro každý případ

⚠️ Typické chytáky

U dvojciferných čísel: rozdíl na desítkách se násobí 10! (o 3 víc na desítkách = o 30 větší číslo)
U magického čtverce: sečti všechna čísla a vyděl počtem řádků — to dá magickou konstantu
Nezapomeň na přenosy u sčítání — když součet přesáhne 9, jednička se přenese do dalšího sloupce
„O jednoho méně" v úlohách s počty — pozor, co přesně je základ (méně než co?)

❌ Nejčastější chyby

Neověřit, jestli VŠECHNY podmínky ze zadání souhlasí — zkontroluj součty řádků i sloupců
U kryptaritmetiky: zapomenout, že různá písmena = různé číslice
Spokojit se s jedním řešením, když CERMAT chce všechna

🧠 Logické úlohy — tabulky a vylučování

🔑 Jak řešit logické úlohy?

🎯 Rady pro CERMAT: Logické úlohy