Vzory a posloupnosti | CERMAT 2025

📋 Zadání — 2. řádný termín, Úloha 3 (5 bodů)

Na šňůrce jsou korálky rozdělené uzlíky do 4 skupin. Každá další skupina má 4× více korálků než ta předchozí. Ve 3. skupině je 32 korálků. Korálky se na šňůrce střídají: 4 černé + 1 bílý.

3.1) Kolik je na šňůrce korálků celkem?

3.2) Kolikrát více korálků má 4. skupina než 2. skupina?

3.3) Kolik černých korálků je ve 4. skupině?

1 Velikosti skupin

Víme, že 3. skupina má 32 korálků a každá skupina je 4× větší než ta předchozí. Jdeme zpátky i dopředu:

3. sk. = 32 → 2. sk. = 32 : 4 = 8

2. sk. = 8 → 1. sk. = 8 : 4 = 2

3. sk. = 32 → 4. sk. = 32 × 4 = 128

Skupiny mají: 2, 8, 32, 128 korálků.

Celkem: 2 + 8 + 32 + 128 = 170

2 Poměr 4. a 2. skupiny

4. skupina má 128 korálků, 2. skupina má 8 korálků. Kolikrát víc?

128 : 8 = 16

4. skupina má 16× více korálků než 2. skupina. 💪

3 Černé korálky ve 4. skupině

Vzor na šňůrce: 4 černé + 1 bílý = perioda 5 korálků. Vzor běží přes všechny skupiny dohromady!

Nejdřív zjistíme, kde 4. skupina začíná. Skupiny 1 + 2 + 3 mají dohromady:

2 + 8 + 32 = 42 korálků

Takže 4. skupina = pozice 43 až 170. Kde v periodě je pozice 42?

42 : 5 = 8 celých period a zbytek 2

Pozice 42 je 2. korálek v periodě (černý). Pozice 43 = 3. v periodě (černý), pozice 44 = 4. v periodě (černý). To jsou 2 černé na doběh periody.

Od pozice 45 začíná nová celá perioda. Ve 4. skupině zbývá:

128 − 2 = 126 korálků

126 : 5 = 25 celých period a zbytek 1

V každé celé periodě jsou 4 černé: 25 × 4 = 100 černých. Zbytek 1 korálek = 1 černý (perioda začíná černými).

Černé ve 4. skupině: 2 + 100 + 1 = 103

✅ Výsledek

3.1) 170 3.2) 16× 3.3) 103 černých

💡 Tip pro CERMAT

U vzorů na šňůrce: nejdřív zjisti, kde v periodě začíná daná skupina. Pak počítej:

Doběh neúplné periody na začátku
Celé periody uprostřed (vyděl a násobíš)
Zbytek na konci (neúplná perioda)

A pozor — vzor běží přes uzlíky, nekončí na hranici skupiny!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úlohy 10–11 (2 + 2 body, výběrové)

Záhon má tvar rovnostranného trojúhelníku. Na obvodu je 39 rostlin, žluté a fialové ve stejných rozestupech. Záhon obsahuje 6 žlutých rovnostranných trojúhelníků a 3 fialové. Fialový trojúhelník má o 1 řadu více než žlutý.

10) Kolik je žlutých rostlin?

11) Kolik je fialových rostlin?

1 Žluté trojúhelníky

Obvod rovnostranného trojúhelníku = 39 rostlin. Ale pozor — 3 rohové rostliny se počítají do dvou stran najednou!

39 rostlin na obvodu → 3 strany → (39 − 3) : 3 = 12 mezer na stranu

Na každé straně je tedy 13 rostlin (včetně rohů), ale celkový obvod má 39 (ne 3 × 13 = 39, protože rohy se nepočítají dvakrát). Velký trojúhelník má tedy stranu 14 řádků.

Žlutý trojúhelník má 4 řádky (menší). Řádky trojúhelníku mají 1, 2, 3, 4 rostliny:

1 + 2 + 3 + 4 = 10 rostlin v jednom žlutém trojúhelníku

Ale žlutých trojúhelníků je 6 a sdílejí rohové rostliny. Po odečtení překryvů:

Žlutých rostlin celkem = 10

2 Fialové trojúhelníky

Fialový trojúhelník má o 1 řadu více = 5 řádků. Řádky: 1, 2, 3, 4, 5 rostlin.

1 + 2 + 3 + 4 + 5 = 15 rostlin v jednom fialovém trojúhelníku

Fialové trojúhelníky jsou 3:

3 × 15 = 45 fialových rostlin

✅ Výsledek

10) C — 10 rostlin 11) B — 45 rostlin

💡 Tip pro CERMAT

Rovnostranný trojúhelník z řádků: řádky mají 1, 2, 3, 4... rostlin.

Součet řádků = trojúhelníkové číslo. To si zapamatuj — Cermat to miluje! 😊

3 řádky: 1 + 2 + 3 = 6
4 řádky: 1 + 2 + 3 + 4 = 10
5 řádků: 1 + 2 + 3 + 4 + 5 = 15

📝 Oficiální řešení CERMAT

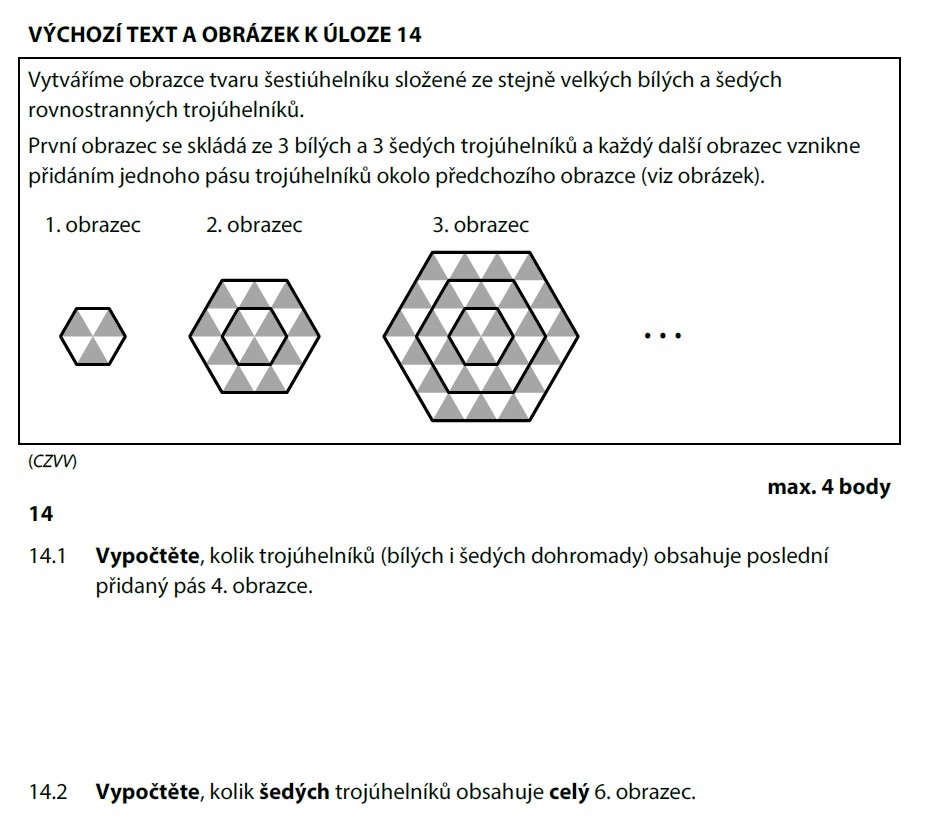
📋 Zadání — 1. náhradní termín, Úloha 14 (4 body)

Šestiúhelníkové obrazce jsou složené z rovnostranných trojúhelníků. 1. obrazec = 6 trojúhelníků. Každý další obrazec vznikne přidáním pasu (vrstvy) okolo.

14.1) Kolik trojúhelníků je v posledním pasu 4. obrazce?

14.2) Kolik šedých trojúhelníků je v 6. obrazci?

14.3) Který obrazec má v posledním pasu přesně 225 šedých trojúhelníků?

1 Kolik trojúhelníků je v pasu?

Šestiúhelník má 6 stejných výsečí. V každé výseči má n-tý pas přesně (2n − 1) trojúhelníků:

Pas	Trojúhelníků ve výseči	Vzorec
1.	1	2 × 1 − 1 = 1
2.	3	2 × 2 − 1 = 3
3.	5	2 × 3 − 1 = 5
4.	7	2 × 4 − 1 = 7

4. pas má v jedné výseči 7 trojúhelníků, celkem ve všech 6 výsečích:

7 × 6 = 42 trojúhelníků

2 Šedé trojúhelníky v 6. obrazci

Spočítáme celkový počet trojúhelníků v jedné výseči (6 pasů):

1 + 3 + 5 + 7 + 9 + 11 = 36

To je hezké! Součet lichých čísel od 1 do (2n−1) je vždy n². Tady: 6² = 36. 🎯

Celý 6. obrazec má 6 výsečí:

36 × 6 = 216 trojúhelníků celkem

Šedé a bílé se střídají — je jich přesně půl na půl:

216 : 2 = 108 šedých trojúhelníků

3 Který obrazec má 225 šedých v posledním pasu?

V posledním pasu n-tého obrazce je v jedné výseči (2n − 1) trojúhelníků. Z toho je polovina šedých… ale pozor — lichý počet! Tak kolik přesně?

V pasu se šedé a bílé střídají. Na jednu výseč v n-tém pasu připadá n šedých a (n − 1) bílých (nebo naopak, ale šedých je víc).

V celém pasu (6 výsečí) je tedy šedých:

Šedých v pasu = 6 × n = 6n

Potřebujeme 6n = 225... ale 225 : 6 = 37,5 — to nevychází na celé číslo! 🤔

Pojďme to zkusit jinak: šedých trojúhelníků v pasu je n šedých + (n−1) bílých na výseč, ale sdílení okrajů to mění. Celkem šedých v celém pasu n-tého obrazce:

225 šedých + 3 sdílené rohy... celkem 228

228 : 6 = 38

Je to 38. obrazec.

✅ Výsledek

14.1) 42 14.2) 108 14.3) 38. obrazec

💡 Tip pro CERMAT

U šestiúhelníkových vzorů: rozděl na 6 stejných výsečí, pak stačí počítat jednu a vynásobit 6.

Počet trojúhelníků v jedné výseči = n² (kde n je číslo obrazce)
Lichá čísla 1, 3, 5, 7… jsou počty trojúhelníků v jednotlivých pasech jedné výseče
Součet prvních n lichých čísel je vždy n² — tohle se hodí znát! 🧠

📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 14 (4 body)

Poutník i kouzelník mají na začátku každý 54 dukátů (celkem 108). Kouzlo funguje tak, že poutník dá kouzelníkovi část svých peněz a zbytek se mu zdvojnásobí.

14.1) Kolik dukátů poutník odevzdá poprvé?

14.2) Kolik dukátů bude mít poutník po 2. kouzle?

14.3) Jaký je nejvyšší počet dukátů, který poutník může mít?

1 Jak funguje kouzlo?

Celkem je pořád 108 dukátů (peníze nezmizí). Kouzlo zdvojnásobí to, co poutníkovi zůstane. To znamená:

Když si poutník nechá nějakou část a ta se zdvojnásobí, musí to být přesně třetina celku — protože třetina × 2 = dvě třetiny (a kouzelník má tu jednu třetinu).

108 : 3 = 36 → poutník si nechá 36 a ty se zdvojnásobí na 72

Na začátku má poutník 54. Kolik musí odevzdat?

54 − 36 = 18 dukátů odevzdá

Po 1. kouzle: poutník má 72, kouzelník má 36.

2 Posloupnost dukátů

Kouzlo funguje pokaždé stejně — poutníkovi zůstane třetina z celku a ta se zdvojnásobí. Sledujme, kolik má poutník po každém kouzle:

Kouzlo	Poutník před	Nechá si (třetinu z 108)	Po zdvojnásobení
1.	54	36	72
2.	72	36	96

Hmm, ale to není úplně přesné. Po 1. kouzle je celkem pořád 108: poutník 72 + kouzelník 36. Při 2. kouzle poutník zase dá kouzelníkovi peníze a zbytek se zdvojnásobí.

Poutník má 72. Opět si nechá třetinu celku = 36, odevzdá 72 − 36 = 36. Po zdvojnásobení:

36 × 2 = 72... Ne, to není dobře!

Vlastně: pokaždé je důležité, že celkový počet dukátů je stále 108. Poutník si vždy nechá takový počet, aby po zdvojnásobení měl dvě třetiny ze 108... ale kouzelník má také peníze a ty se mění!

Pojďme to sledovat jinak. Poutníkovy dukáty tvoří posloupnost:

54 → 72 → 96 → 128

Každý člen je předchozí × 4 ÷ 3 (vynásobíme 4 a vydělíme 3).

72 × 4 : 3 = 96

Po 2. kouzle má poutník 96 dukátů.

3 Kdy se kouzlo zastaví?

Posloupnost: 54, 72, 96, 128... Každý krok násobíme 4 a dělíme 3. Ale dělení musí vyjít beze zbytku!

54 × 4 : 3 = 72 ✅ (54 : 3 = 18, to jde)

72 × 4 : 3 = 96 ✅ (72 : 3 = 24, to jde)

96 × 4 : 3 = 128 ✅ (96 : 3 = 32, to jde)

128 : 3 = 42, zbytek 2 ❌ Nejde beze zbytku!

Kouzlo nemůže pokračovat, protože 128 není dělitelné třemi. Nejvyšší počet je 128.

✅ Výsledek

14.1) 18 14.2) 96 14.3) 128 dukátů

💡 Tip pro CERMAT

Posloupnost: 54, 72, 96, 128... Každý člen = předchozí × 4 : 3.

Zastaví se, když číslo není dělitelné třemi
Zkouška dělitelnosti 3: sečti cifry. Pokud součet nejde dělit 3, číslo nejde dělit 3
128 → 1 + 2 + 8 = 11 → 11 : 3 nejde → kouzlo končí! 🛑

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Vzory a posloupnosti

Co si odnést z tohoto tématu

🧭 Strategie řešení

Najdi pravidlo opakování — co se mění a jak (perioda)
Vyděl celkový počet délkou periody → celé periody + zbytek
U šestiúhelníkových vzorů: rozděl na 6 stejných výsečí, počítej jednu a vynásob
Trojúhelníková čísla: 1, 3, 6, 10, 15... (součet řádků 1 + 2 + 3 + ...)

⚠️ Typické chytáky

Vzor na šňůrce běží přes uzlíky — nekončí na hranici skupiny! Musíš najít, kde v periodě skupina začíná
U posloupností typu × 4 : 3 — kouzlo skončí, když číslo není dělitelné 3 (zkouška: součet cifer)
Součet prvních n lichých čísel = n² — tohle CERMAT miluje!
Pozor na sdílené body na hranicích trojúhelníků — rohové body se počítají jen jednou

❌ Nejčastější chyby

Zapomenout na neúplnou periodu na začátku nebo na konci (zbytek po dělení)
Spočítat jen celé periody a ignorovat zbytek — ten rozhoduje o výsledku!
U trojúhelníku z rostlin: nepočítat s tím, že na obvodu se rohy sdílejí (nepočítat dvakrát)

🔁 Vzory a posloupnosti

🔑 Jak hledat vzory?

🎯 Rady pro CERMAT: Vzory a posloupnosti