
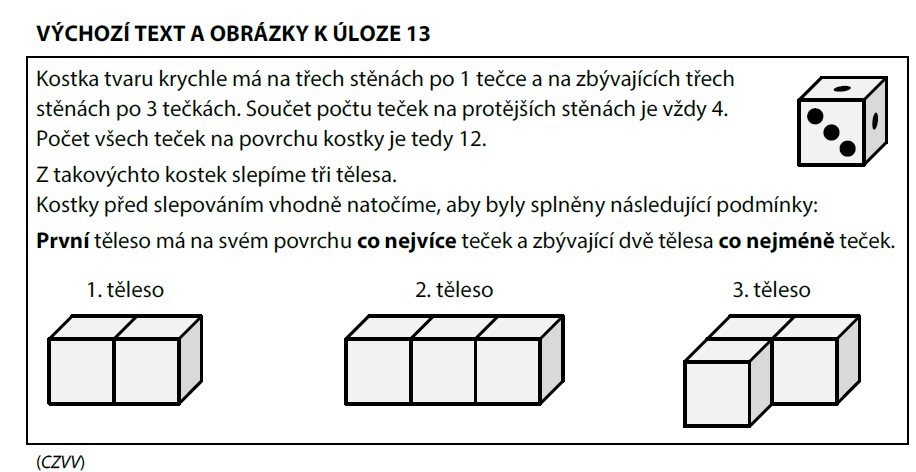

Každá kostka má 6 stěn. Sečteme tečky na všech stěnách:
Důležité pravidlo: protější stěny mají dohromady vždy 1 + 3 = 4.
Když dvě kostky slepíme, dvě stěny (jedna z každé kostky) se skryjí — ty pak nevidíme.
Chceme co nejvíc teček na povrchu. Musíme tedy schovat stěny s co nejmenším počtem teček!
Slepíme kostky tak, aby se u spoje schovaly stěny s 1 tečkou (z každé kostky jedna):
Odpověď: C) 22 teček
Teď naopak — chceme co nejméně teček na povrchu. Schovej stěny s co nejvíc tečkami!
Tvar L: 3 kostky v řadě + 1 kostka na konci kolmo. Počet spojů: 3 spojení (= 6 schovaných stěn).
Chceme skrýt trojky. Ale pozor — u každého spoje se skryjí 2 protější stěny (jedna z každé kostky), a protější stěny dají vždy součet 4. Takže u spoje schováme vždy 4 tečky (pár 1+3).
Ale v rozích tvaru L se některé kostky dotýkají dvakrát, takže tam můžeme optimalizovat. Spočítáme pečlivě:
Ale u rohové kostky (ta v ohybu L) se můžeme dostat na lepší variantu rozmístění. Přesný výpočet dává:
Odpověď: E) 26 teček
Tvar T: 3 kostky v řadě + 1 kostka uprostřed nahoře. Opět 3 spojení, ale jiné rozvržení.
Prostřední kostka se dotýká dvou sousedů (vlevo, vpravo) a jednoho nahoře. Ta má nejvíc schovaných stěn.
U tvaru T můžeme schovat ještě víc trojek díky lepšímu uspořádání. Výsledek:
Odpověď: D) 24 teček
- Pro MAX teček: slepuj stěny s nejmenším počtem teček (jedničky) — schováš málo.
- Pro MIN teček: slepuj stěny s největším počtem teček (trojky) — schováš hodně.
- Pamatuj: protější stěny mají vždy součet 4 (1+3), takže u každého spoje zmizí přesně 4 tečky (pár), pokud si nemůžeš vybrat orientaci.
- U složitějších tvarů (L, T) záleží i na tom, jak kostky natočíš — vyzkoušej víc variant!

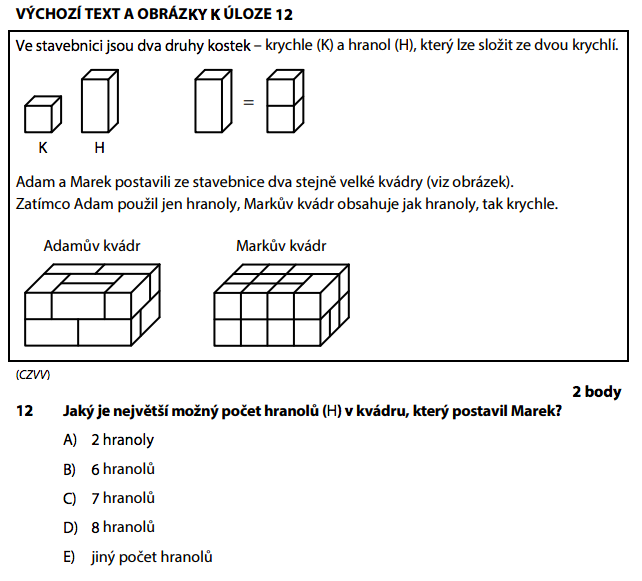
Adam staví kvádr jen z hranolů. Každý hranol zabírá místo 2 krychlí. To znamená, že celkový počet „krychlových míst" v kvádru musí být sudý.
Například kvádr 2×3×2 = 12 krychlových míst → dá se vyplnit 6 hranoly.
Marek staví stejně velký kvádr, ale smí použít i krychle. Chceme, aby měl co nejvíc hranolů.
Strategie: vyplň co nejvíc místa hranoly a zbytek doplň krychlemi.
Klíčové je, jak velký je Adamův kvádr. Nejmenší kvádr celý z hranolů je třeba 2×2×2 = 8 míst = 4 hranoly. Ale Marek by pak měl max 4 hranoly (to samé). Zkusíme větší: 2×2×3 = 12 míst = 6 hranolů pro Adama.
Podle zadání (konkrétní rozměry kvádru z obrázku v testu) vychází, že Marek může do svého kvádru umístit nejvýše 8 hranolů a zbytek doplní krychlemi.
Hranoly pokládej rovnoběžně, aby se vešly vedle sebe a zaplnily co nejvíc prostoru:
- Hranoly pokládej rovnoběžně, aby zaplnily co nejvíc místa.
- Krychle používej jen na vyplnění zbylých lichých míst.
- Vždy si nakresli kvádr a zkus do něj hranoly „skládat" jako Lego.

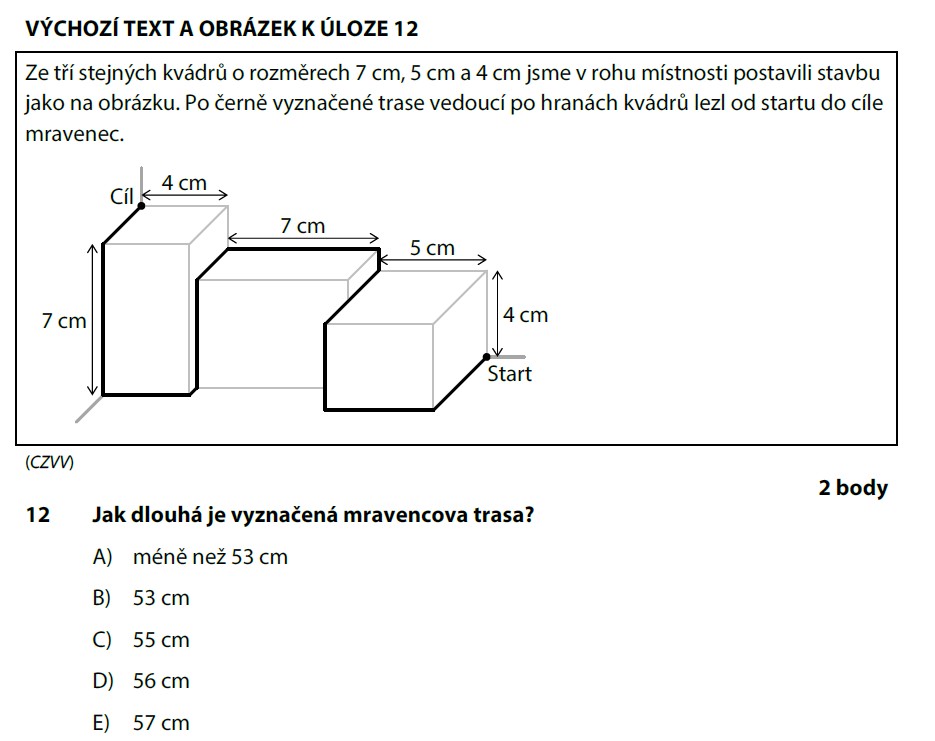
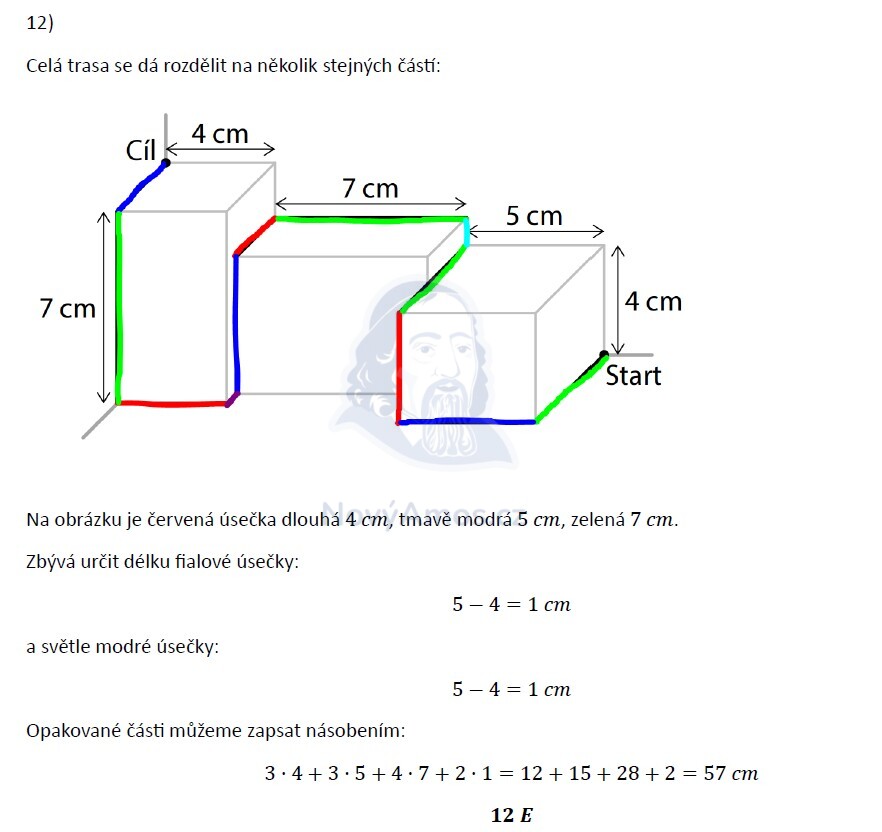
Mravenec leze po hranách kvádrů. Každá hrana má délku 7, 5 nebo 4 cm. Projdeme trasu krok za krokem a rozlišíme úseky podle směru:
| Barva úseku | Délka hrany | Kolikrát | Celkem |
|---|---|---|---|
| 🔴 červená | 4 cm | 3× | 12 cm |
| 🔵 modrá | 5 cm | 3× | 15 cm |
| 🟢 zelená | 7 cm | 4× | 28 cm |
| 🟣 fialová | 1 cm | 2× | 2 cm |
Fialové úseky (1 cm) vznikají tam, kde mravenec přelézá z jednoho kvádru na druhý — je to rozdíl hran.
Teď stačí všechno sečíst:
- U trasy po hranách si rozlož cestu na úseky podle směrů a sečti.
- Pozor na krátké úseky, kde mravenec přelézá z jednoho kvádru na druhý — snadno se přehlédnou!
- Zkontroluj si výsledek tím, že si cestu projdeš prstem po obrázku.
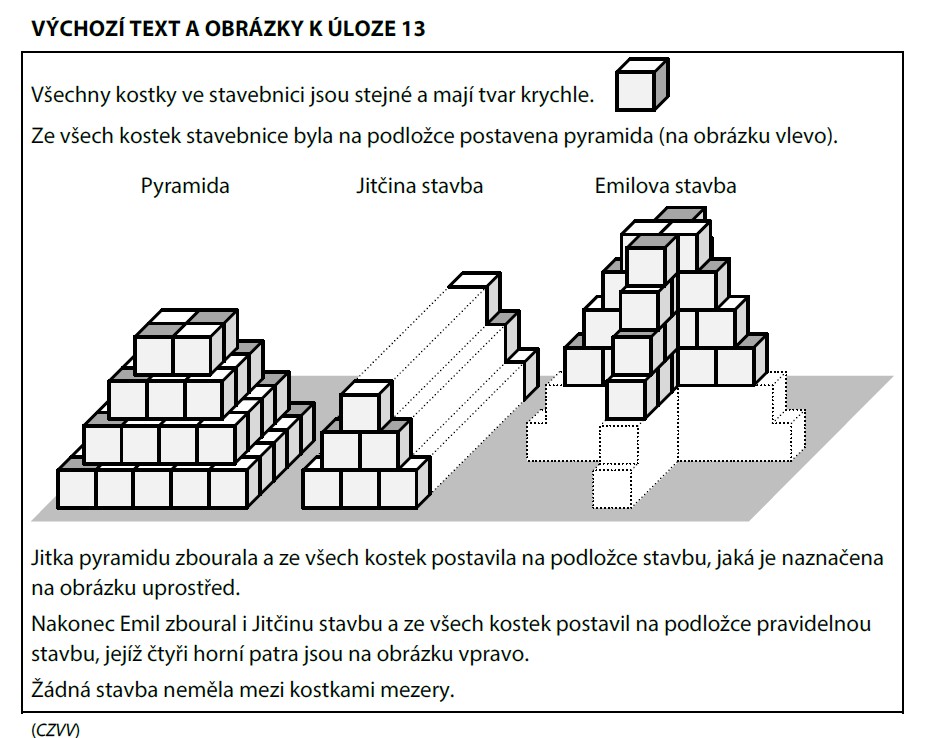

Pyramida má 5 pater. Každé patro je čtverec — počítáme kostky v každém patře:
| Patro | Rozměr | Počet kostek |
|---|---|---|
| 5. (vrchol) ⬆️ | 1 × 1 | 1 |
| 4. | 2 × 2 | 4 |
| 3. | 3 × 3 | 9 |
| 2. | 4 × 4 | 16 |
| 1. (spodek) ⬇️ | 5 × 5 | 25 |
| Celkem | 55 kostek | |
To je součet čtverců: 1² + 2² + 3² + 4² + 5² = 55. Tohle si zapamatuj! 😉
Skrytá kostka = taková, kterou nevidíš z žádné strany (ani shora, ani ze stran). Jsou to kostky, které mají nad sebou, pod sebou i kolem sebe další kostky.
Počítáme po patrech — v každém patře hledáme kostky, které mají kolem sebe ze všech stran další kostky:
| Patro | Rozměr | Vnitřní kostky | Proč? |
|---|---|---|---|
| 5. (1×1) | 1 × 1 | 0 | Jen 1 kostka, vidíme ji shora |
| 4. (2×2) | 2 × 2 | 0 | Všechny na kraji |
| 3. (3×3) | 3 × 3 | 1 | Prostřední kostka (1×1 uvnitř) |
| 2. (4×4) | 4 × 4 | 4 | Vnitřní čtverec 2×2 |
| 1. (5×5) | 5 × 5 | 9 | Vnitřní čtverec 3×3 |
| Celkem skrytých | 14 kostek | ||
Jitka zbourala pyramidu (55 kostek) a postavila svou stavbu. Podle obrázku v zadání má stavba určitý tvar.
Kostky na podložce = kostky, které se dotýkají spodní desky. Podle tvaru Jitčiny stavby:
Odpověď: F) více než 26 — konkrétně 27 kostek se dotýká podložky.
Emil přestavěl Jitčinu stavbu na pravidelnou stavbu (všech 55 kostek). Emilova stavba má 6 pater s počty kostek v každém patře:
| Patro (shora) | Počet kostek |
|---|---|
| 6. (vrchol) | 4 |
| 5. | 6 |
| 4. | 8 |
| 3. | 10 |
| 2. | 12 |
| 1. (spodek) | 14 |
| Spodní 2 patra | 12 + 14 = 26 |
- Pyramida = součet čtverců: 1² + 2² + 3² + 4² + 5² = 55. Tohle si zapamatuj!
- Skryté kostky hledej tak, že z každého patra odečteš okrajový rámeček. Vnitřní čtverec je vždy o 2 menší na každé straně.
- U přestavěných staveb si vždy ověř, že máš stejný počet kostek — nic se nepřidává ani neubírá!
- Cermat miluje pyramidy a počítání skrytých kostek — tohle je klasická „Cermatovina"! 🧊


🎯 Rady pro CERMAT: Prostorová představivost
Co si odnést z tohoto tématu
- Počítej po patrech — zdola nahoru. Každé patro je čtverec nebo obdélník
- U kostek s tečkami: celkový počet teček − schované tečky = viditelné tečky
- U tras po hranách: rozlož cestu na úseky podle směrů a sečti
- Pyramida z N pater = součet čtverců: 1² + 2² + ... + N²
- Skryté kostky uvnitř — ty, které nevidíš z žádné strany! Hledej je odečtením okrajového rámečku
- Protější stěny kostky mají konstantní součet — u spoje zmizí vždy tento pár
- Pro MAX teček: slepuj stěny s nejmenším počtem; pro MIN teček: slepuj stěny s největším počtem
- U přestavěných staveb si ověř stejný počet kostek — nic se nepřidává ani neubírá
- Zapomenout na kostky schované pod jinými — při pohledu shora je nevidíš
- U trasy mravence přehlédnout krátké úseky při přelézání z jednoho kvádru na druhý
- Při počítání pater pyramidy špatně spočítat rozměr — 5. patro má 5×5 = 25, ne 5