Obsahy ve čtvercové síti

📋 Zadání — 1. řádný termín, Úloha 12 (2 body, výběrová)

Ve čtvercové síti (1 čtvereček = 1 cm²) jsou narýsovány trojúhelník ABC a trojúhelník KLM. O kolik cm² se liší jejich obsahy?

  Trojúhelník ABC              Trojúhelník KLM
  (ve čtvercové síti 4×4)      (ve čtvercové síti 4×3)

  ·───·───·───·───·            ·───·───·───·───·
  │╲  │   │   │   │            │   │   │  ╱│   │
  │  ╲│   │   │   │            │   │   │╱  │   │
  ·───·───·───·───·            ·───·───·───·───·
  │   │ ╲ │   │   │            │  ╱│   │   │   │
  │   │  ╲│   │   │            │╱  │   │   │   │
  ·───·───·───·───·            ·───·───·───·───·
  │   │   │╲  │   │            │   │   │   │   │
  │   │   │  ╲│   │            │   │   │   │   │
  ·───·───·───·───·            ·───·───·───·───·
  │   │   │   │╲  │
  │   │   │   │  ╲│
  ·───·───·───·───·

Možnosti: A) 1 cm² B) 2 cm² C) 3 cm² D) 4 cm²

1 Obsah trojúhelníku ABC

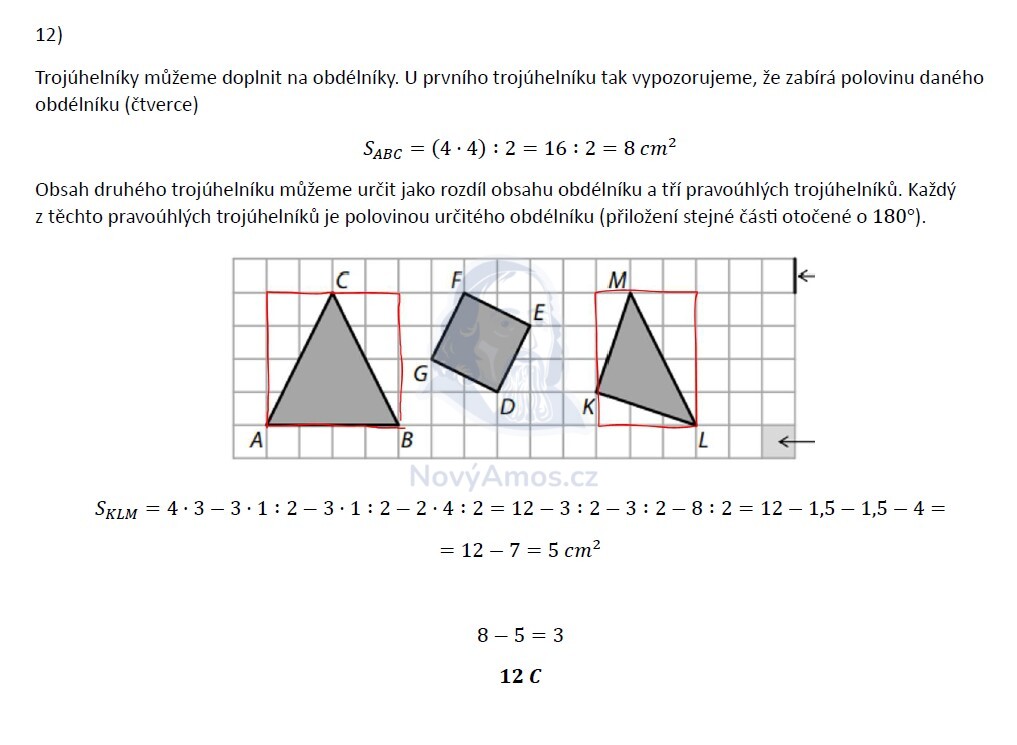
Trojúhelník ABC má základnu 4 cm a výšku 4 cm. U pravoúhlého trojúhelníku (nebo trojúhelníku, kde jednu stranu vidíme jako základnu) použijeme jednoduchý vzorec:

obsah = základna × výška ÷ 2

obsah ABC = 4 × 4 ÷ 2 = 8 cm²

Představ si to tak: trojúhelník ABC zabírá přesně polovinu čtverce 4 × 4 = 16 čtverečků. Polovina z 16 je 8.

2 Obsah trojúhelníku KLM

KLM není tak jednoduchý — nemá pravý úhel u mřížky. Použijeme metodu obdélník minus trojúhelníky:

Obkreslíme KLM nejmenším obdélníkem: 4 × 3 = 12 cm²

  ┌───────────────┐
  │ ╲  T₁  │  ╱T₂│   T₁ = pravoúhlý trojúhelník nahoře vlevo
  │   ╲    │╱    │   T₂ = pravoúhlý trojúhelník nahoře vpravo
  ├────·KLM·─────┤   T₃ = pravoúhlý trojúhelník dole
  │  ╱       ╲   │
  │╱    T₃    ╲  │
  └───────────────┘

Odečteme 3 rohové trojúhelníky:

T₁ = 4 × 2 ÷ 2 = 4 cm²

T₂ = 1 × 3 ÷ 2 = 1,5 cm²

T₃ = 3 × 1 ÷ 2 = 1,5 cm²

obsah KLM = 12 − 4 − 1,5 − 1,5 = 5 cm²

3 Rozdíl obsahů

Teď už jen odečteme:

8 − 5 = 3 cm²

Obsahy trojúhelníků se liší o 3 cm².

✅ Výsledek

Rozdíl = 3 cm² (odpověď C)

💡 Tip pro CERMAT

U trojúhelníku na čtvercové síti existují 2 metody:

Metoda 1: základna × výška ÷ 2 — funguje, když vidíš základnu a výšku přímo na mřížce
Metoda 2: obdélník minus trojúhelníky — funguje vždy, i pro šikmé tvary!
Použij tu, která je jednodušší pro daný obrazec. ABC šlo přímo, KLM potřeboval obdélník.

📝 Oficiální řešení CERMAT

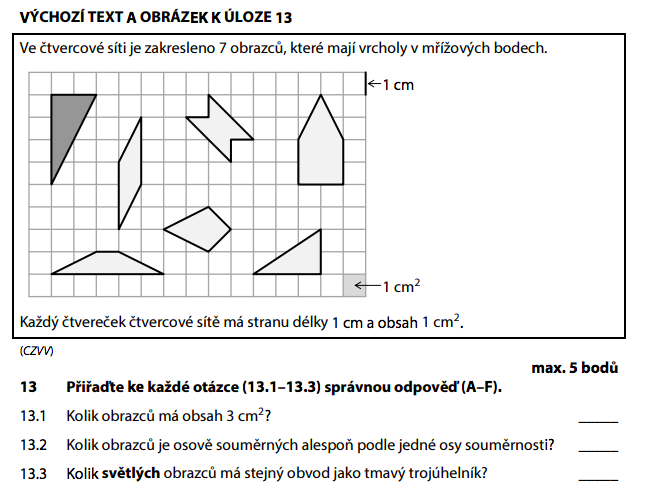
📋 Zadání — 2. řádný termín, Úloha 13 (5 bodů, přiřazovací)

Ve čtvercové síti (1 čtvereček = 1 cm²) je nakresleno 7 obrazců. Ke každé otázce přiřaď správnou odpověď.

Obrazec	Typ
🔵 Tmavý trojúhelník	trojúhelník (polovina 4 × 2)
🔴 Červený čtyřúhelník	obecný čtyřúhelník
🔷 Modrý šestiúhelník	pravidelný šestiúhelník
🟢 Zelený pětiúhelník	pětiúhelník
🟩 Zelený trojúhelník	trojúhelník (polovina 3 × 2)
🟣 Fialový lichoběžník	lichoběžník
🟡 Žlutý čtyřúhelník	obecný čtyřúhelník

13.1) Kolik obrazců má obsah 3 cm²?

13.2) Kolik obrazců je osově souměrných?

13.3) Kolik světlých obrazců má stejný obvod jako tmavý trojúhelník?

Odpovědi: A) 1 B) 2 C) 3 D) 3 E) 4 F) 5 G) 6 H) 7

1 Počítáme obsahy všech obrazců

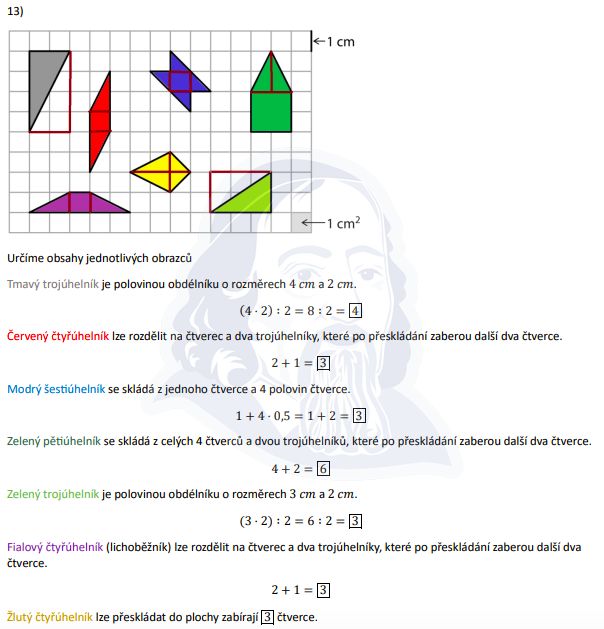
Pro každý obrazec použijeme jednu z metod — buď přímo základna × výška ÷ 2 (u trojúhelníků), nebo obdélník minus trojúhelníky (u složitějších tvarů).

Obrazec	Výpočet	Obsah
🔵 Tmavý trojúhelník	4 × 2 ÷ 2	4 cm²
🔴 Červený čtyřúhelník	obdélník − rohy	3 cm²
🔷 Modrý šestiúhelník	obdélník − rohy	3 cm²
🟢 Zelený pětiúhelník	obdélník − rohy	6 cm²
🟩 Zelený trojúhelník	3 × 2 ÷ 2	3 cm²
🟣 Fialový lichoběžník	obdélník − rohy	3 cm²
🟡 Žlutý čtyřúhelník	obdélník − rohy	3 cm²

Dva obrazce mají jiný obsah: tmavý trojúhelník (4 cm²) a zelený pětiúhelník (6 cm²). Všechny ostatní mají 3 cm².

2 Otázka 13.1: Kolik obrazců má obsah 3 cm²?

Podíváme se do tabulky — obsah 3 cm² mají:

🔴 červený + 🔷 modrý + 🟩 zelený troj. + 🟣 fialový + 🟡 žlutý = 5 obrazců

Všechny kromě tmavého trojúhelníku (4 cm²) a zeleného pětiúhelníku (6 cm²).

3 Otázka 13.2: Kolik obrazců je osově souměrných?

Osová souměrnost znamená, že obrazec můžeš přeložit přes osu a obě poloviny se přesně překryjí — jako motýl.

Projdeme každý obrazec:

Obrazec	Osově souměrný?
🔵 Tmavý trojúhelník	❌ Ne
🔴 Červený čtyřúhelník	❌ Ne
🔷 Modrý šestiúhelník	✅ Ano
🟢 Zelený pětiúhelník	✅ Ano
🟩 Zelený trojúhelník	❌ Ne
🟣 Fialový lichoběžník	✅ Ano
🟡 Žlutý čtyřúhelník	✅ Ano

Osově souměrných = 4 obrazce

4 Otázka 13.3: Obvod jako tmavý trojúhelník

Spočítáme obvod tmavého trojúhelníku — délky jeho stran na čtvercové síti. Pak porovnáme s ostatními světlými obrazci.

Tmavý trojúhelník má strany podél mřížky a šikmo (úhlopříčky). Porovnáváme obvody všech světlých obrazců.

Světlé obrazce se stejným obvodem = 3 obrazce

Trik: na čtvercové síti spočítej délku každé strany — vodorovné a svislé jsou jednoduché (počet čtverečků), šikmé strany přes úhlopříčku čtverečku jsou delší.

✅ Výsledek

13.1) F (5) 13.2) E (4) 13.3) D (3)

💡 Tip pro CERMAT

U přiřazovacích úloh s více obrazci:

Spočítej VŠECHNY hodnoty najednou do tabulky — pak snadno odpovíš na každou otázku!
Nenech se zmást tím, že obrazce vypadají různě — obsah 3 cm² může mít trojúhelník i šestiúhelník.
U osové souměrnosti si představ, že tvar skládáš napůl — obě poloviny se musí přesně překrýt.
U obvodu pozor: šikmá strana přes čtvereček je delší než strana podél mřížky!

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Obsahy ve čtvercové síti

Co si odnést z tohoto tématu

🧭 Strategie řešení

Metoda 1: základna × výška ÷ 2 — použij, když vidíš základnu a výšku přímo na mřížce
Metoda 2: obkresli obrazec obdélníkem a odečti rohové trojúhelníky — funguje vždy!
U přiřazovacích úloh spočítej VŠECHNY hodnoty najednou do tabulky — pak snadno odpovíš na každou otázku
Obsah trojúhelníku = polovina obdélníku se stejnou základnou a výškou

⚠️ Typické chytáky

Různé tvary mohou mít stejný obsah — trojúhelník i šestiúhelník mohou mít 3 cm²
Osová souměrnost: představ si, že tvar skládáš napůl — obě poloviny se musí přesně překrýt
U obvodu pozor: šikmá strana přes čtvereček je DELŠÍ než strana podél mřížky (úhlopříčka > strana)

❌ Nejčastější chyby

Zapomenout vydělit dvěma u trojúhelníku (základna × výška je obsah obdélníku, ne trojúhelníku!)
Při metodě obdélník minus trojúhelníky — přehlédnout jeden z rohových trojúhelníků
Zaměnit obsah a obvod — CERMAT se může ptát na obojí u stejného tvaru

🔲 Obsahy ve čtvercové síti

🔑 Jak na obsah nepravidelného tvaru?

🎯 Rady pro CERMAT: Obsahy ve čtvercové síti