Obvody — jednoduché i složité tvary

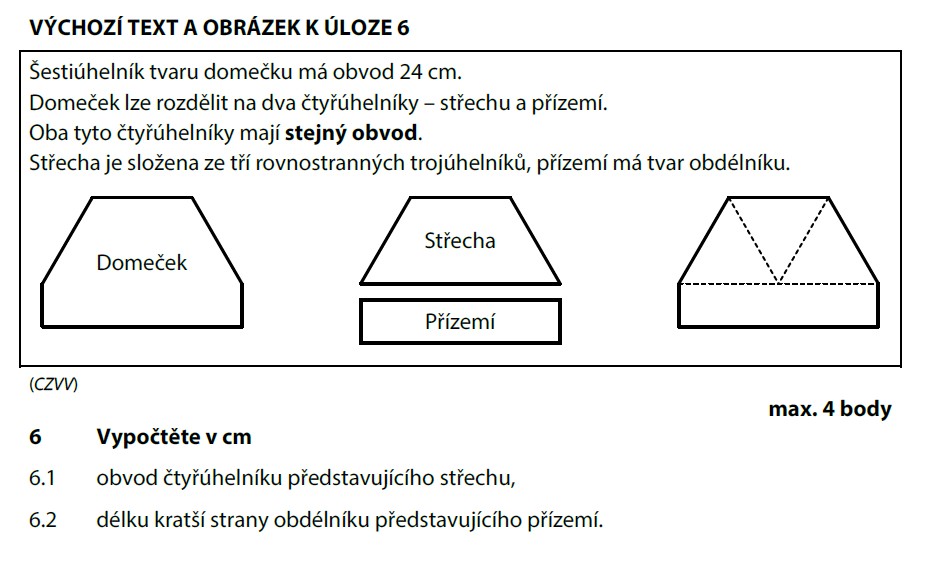
📋 Zadání — 1. řádný termín, Úloha 6 (4 body)

Šestiúhelník tvaru „domečku" je složený z rovnostranných trojúhelníků. Jeho obvod je 24 cm (6 stran trojúhelníku).

6.1) Jaký je obvod „střechy" (lichoběžníku)?

6.2) Obdélník má stejný obvod jako lichoběžník. Delší strana = 2× strana trojúhelníku. Kratší strana = ?

1 Zjistíme délku strany trojúhelníku

Šestiúhelník má obvod 24 cm a skládá se z 6 stran trojúhelníku. Všechny strany jsou stejně dlouhé (rovnostranný trojúhelník!):

24 : 6 = 4 cm

Jedna strana trojúhelníku měří 4 cm.

2 Obvod střechy a kratší strana obdélníku

Střecha (lichoběžník) má obvod tvořený 5 stranami trojúhelníku:

Obvod střechy = 5 × 4 = 20 cm

Obdélník se stejným obvodem 20 cm — delší strana je 2× strana trojúhelníku:

Delší strana = 2 × 4 = 8 cm

Obvod obdélníku = 2 × (delší + kratší). Odtud kratší strana:

Kratší strana = (20 − 2 × 8) : 2 = (20 − 16) : 2 = 2 cm

✅ Výsledek

6.1) 20 cm 6.2) 2 cm

💡 Tip pro CERMAT

Spočítej, kolik stran trojúhelníku tvoří obvod daného tvaru — stačí pak jen násobit! Rovnostranné trojúhelníky mají všechny strany stejné, takže si ušetříš práci.

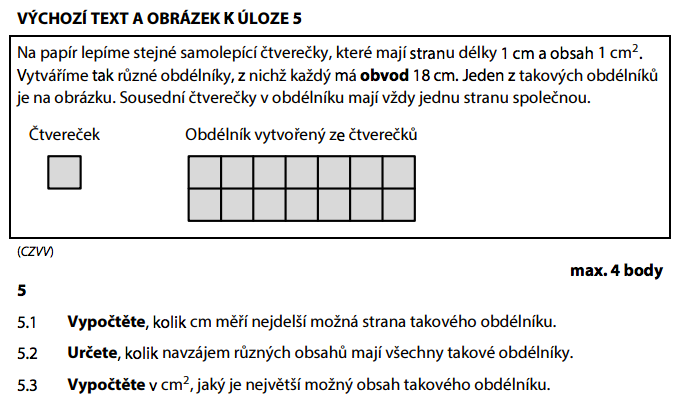
📋 Zadání — 2. řádný termín, Úloha 5 (4 body)

Lepíme čtverečky 1×1 cm do obdélníků s obvodem 18 cm.

5.1) Jaká je nejdelší možná strana?

5.2) Kolik různých obsahů můžeme dostat?

5.3) Jaký je největší obsah?

1 Najdeme všechny obdélníky s obvodem 18 cm

Obvod obdélníku = 2 × (délka + šířka). Součet sousedních stran tedy je:

18 : 2 = 9

Hledáme dvojice celých čísel, které dají dohromady 9:

1 + 8, 2 + 7, 3 + 6, 4 + 5

To jsou 4 různé obdélníky: 1×8, 2×7, 3×6, 4×5.

2 Odpovídáme na všechny otázky

Nejdelší strana: z obdélníku 1×8 → strana 8 cm.

Spočítáme obsahy každého obdélníku:

1 × 8 = 8 2 × 7 = 14 3 × 6 = 18 4 × 5 = 20

Různé obsahy: 8, 14, 18, 20 → celkem 4 různé.

Největší obsah: 4 × 5 = 20 cm². Všimni si — čím blíže ke čtverci, tím větší obsah!

✅ Výsledek

5.1) 8 cm 5.2) 4 5.3) 20 cm²

💡 Tip pro CERMAT

Při stejném obvodu má ČTVEREC vždy největší obsah. Tohle CERMAT testuje často! Když hledáš největší obsah, vyber obdélník co nejbližší čtverci.

📝 Oficiální řešení CERMAT

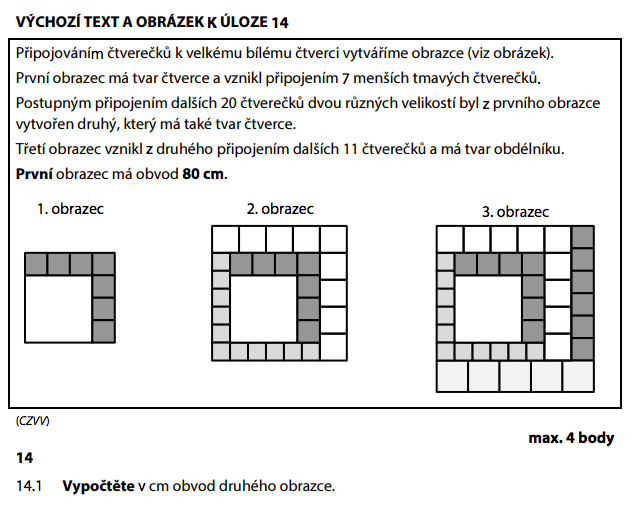
📋 Zadání — 2. řádný termín, Úloha 14 (4 body)

Čtverečkové obrazce — 1. obrazec je čtverec (obvod 80 cm). 2. obrazec vznikne přidáním 20 čtverečků. 3. obrazec přidáním 11 čtverečků (vznikne obdélník).

14.1) Jaký je obvod 2. obrazce?

14.2) Jaký je rozdíl sousedních stran 3. obrazce?

14.3) Jaká je délka lomené čáry?

1 Zjistíme velikost čtverečků

1. obrazec je čtverec s obvodem 80 cm. Strana čtverce:

80 : 4 = 20 cm

Čtverec je složený z tmavých a světlých čtverečků. Tmavý čtvereček: 4 na stranu → strana = 20 : 4 = 5 cm. Světlý čtvereček: 5 na stranu → strana = 20 : 5 = 4 cm.

2 Obvod 2. obrazce

2. obrazec má stranu složenou z 6 tmavých čtverečků:

Strana = 6 × 5 = 30 cm

Je to opět čtverec, takže:

Obvod = 4 × 30 = 120 cm

3 3. obrazec a lomená čára

3. obrazec je obdélník o stranách 35 cm a 37 cm. Rozdíl sousedních stran:

37 − 35 = 2 cm

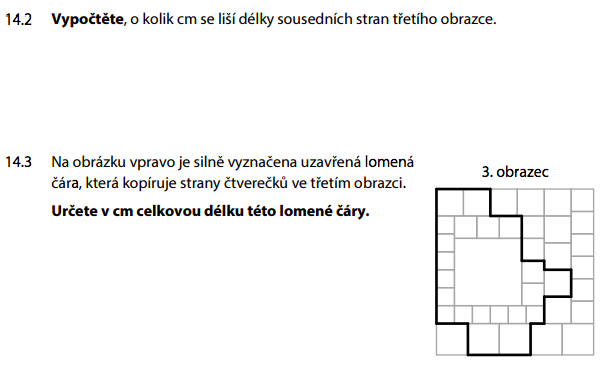
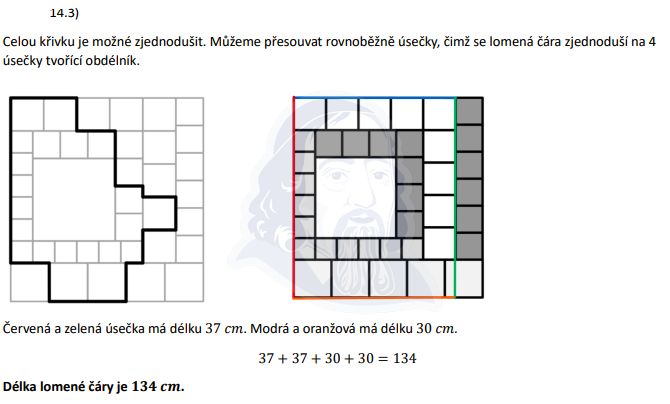
Lomená čára (po hranách čtverečků) má stejnou délku jako obvod obdélníku, který ji obaluje! Rovnoběžné odskoky se vzájemně vyruší:

Lomená čára = 37 + 37 + 30 + 30 = 134 cm

✅ Výsledek

14.1) 120 cm 14.2) 2 cm 14.3) 134 cm

💡 Tip pro CERMAT

Klíčový trik — lomená čára podél čtverečků má STEJNOU délku jako obvod obdélníku, do kterého se vejde! Rovnoběžné odskoky se vzájemně vyruší. Tohle je oblíbená „Cermatovina"!

📝 Oficiální řešení CERMAT

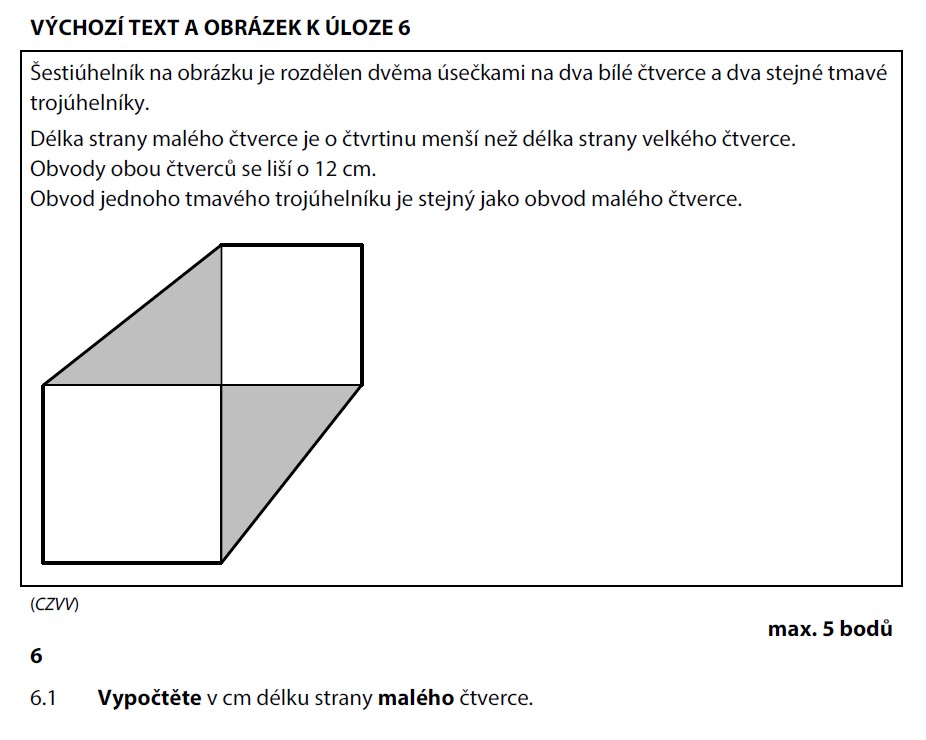
📋 Zadání — 1. náhradní termín, Úloha 6 (5 bodů)

Šestiúhelník se skládá ze dvou čtverců a dvou trojúhelníků. Malý čtverec je o čtvrtinu menší než velký. Obvody čtverců se liší o 12 cm. Obvod trojúhelníku = obvod malého čtverce.

6.1) Strana malého čtverce?

6.2) Obvod velkého čtverce?

6.3) Kolikrát je obvod šestiúhelníku větší než obvod trojúhelníku?

1 Pracujeme s dílky

„O čtvrtinu menší" znamená: velký = 4 dílky, malý = 3 dílky. Jejich obvody (čtverec má 4 strany):

Velký obvod = 16 dílků, Malý obvod = 12 dílků

Rozdíl obvodů = 16 − 12 = 4 dílky = 12 cm:

12 : 4 = 3 cm (1 dílek)

2 Strany a obvody čtverců

Strana malého čtverce = 3 dílky:

3 × 3 = 9 cm

Strana velkého čtverce = 4 dílky:

4 × 3 = 12 cm

Obvod velkého čtverce:

4 × 12 = 48 cm

3 Obvod šestiúhelníku a poměr

Obvod trojúhelníku = obvod malého čtverce = 36 cm (12 dílků × 3). Trojúhelník má dvě strany shodné se čtverci (12 cm a 9 cm), takže nejdelší strana:

36 − 12 − 9 = 15 cm

Obvod šestiúhelníku (vnější strany):

2 × 15 + 2 × 12 + 2 × 9 = 30 + 24 + 18 = 72 cm

Poměr: 72 : 36 = 2× větší.

✅ Výsledek

6.1) 9 cm 6.2) 48 cm 6.3) 2× větší

💡 Tip pro CERMAT

Když CERMAT řekne „o čtvrtinu menší", mysli v dílcích: velký = 4 dílky, malý = 3 dílky. Dílek je tvůj nejlepší kamarád — funguje všude v geometrii!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 11 (2 body)

Obdélníkový záhon, délka = 3× šířka, obvod 16 m. Po obvodu sázíme květiny s rozestupem 40 cm. O kolik se liší počet květin na kratší a delší straně?

1 Rozměry záhonu

Délka = 3× šířka. Součet sousedních stran = šířka + 3× šířka = 4 dílky:

16 : 2 = 8 m → 4 dílky = 8 m → 1 dílek = 2 m

Šířka = 2 m = 200 cm, délka = 6 m = 600 cm.

2 Počet květin na každé straně

Pozor! Rozestupy a body (květiny) nejsou totéž. N rozestupů = N+1 květin!

Kratší: 200 : 40 = 5 rozestupů = 6 květin

Delší: 600 : 40 = 15 rozestupů = 16 květin

3 Rozdíl

16 − 6 = 10 květin

Na delší straně je o 10 květin víc než na kratší.

✅ Výsledek

O 10 květin (odpověď B)

⚠️ CERMAT chyták

Rozestupy vs. body: N rozestupů = N+1 květin! Nezapomeň přičíst rohovou květinu. Taky si hlídej převod jednotek: 16 m a rozestupy 40 cm — musíš vše převést na stejné jednotky!

📝 Oficiální řešení CERMAT

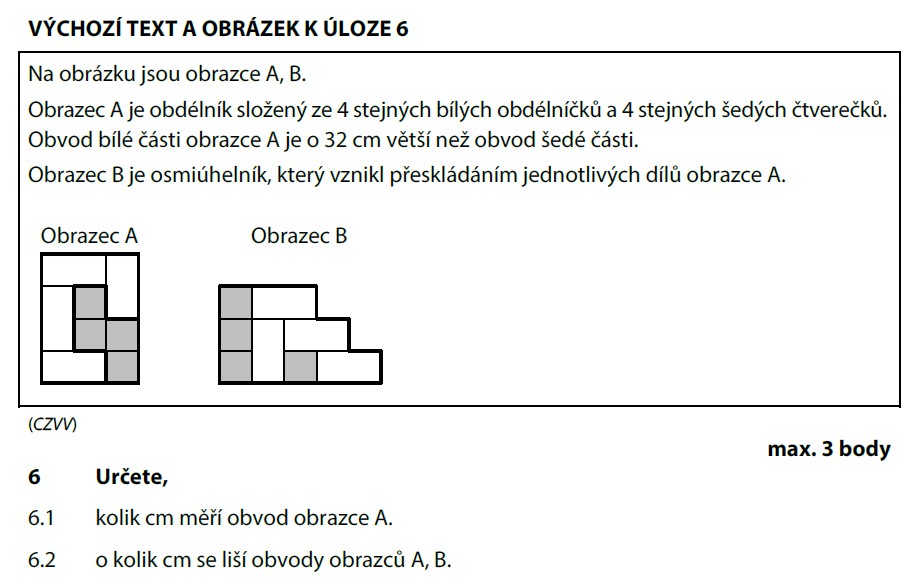
📋 Zadání — 2. náhradní termín, Úloha 6 (3 body)

Obrazce A (obdélník ze 4 bílých obdélníčků a 4 šedých čtverečků) a B (osmiúhelník přeskládáním stejných dílů). Obvod bílé části je o 32 cm větší než šedé.

6.1) Obvod obrazce A?

6.2) Rozdíl obvodů obrazců A a B?

1 Zjistíme velikost strany čtverečku

Spočítáme strany čtverečků ve vnějším obvodu šedé a bílé části:

Šedá = 10 stran, Bílá = 18 stran

Rozdíl obvodů je 8 stran čtverečku = 32 cm:

32 : 8 = 4 cm (strana čtverečku)

2 Obvody obrazců A a B

Obvod obrazce A (kolem celého obdélníku):

Obvod A = 14 stran × 4 = 56 cm

Obrazec B (osmiúhelník po přeskládání) má jiný tvar, ale stejný obsah:

Obvod B = 16 stran × 4 = 64 cm

Rozdíl obvodů:

64 − 56 = 8 cm

✅ Výsledek

6.1) 56 cm 6.2) 8 cm

💡 Tip pro CERMAT

Při přeskládání se mění obvod, i když obsah zůstane stejný! Vnější tvar se změní — některé strany, co byly uvnitř, se dostanou ven. Vždy si pečlivě spočítej strany nového tvaru.

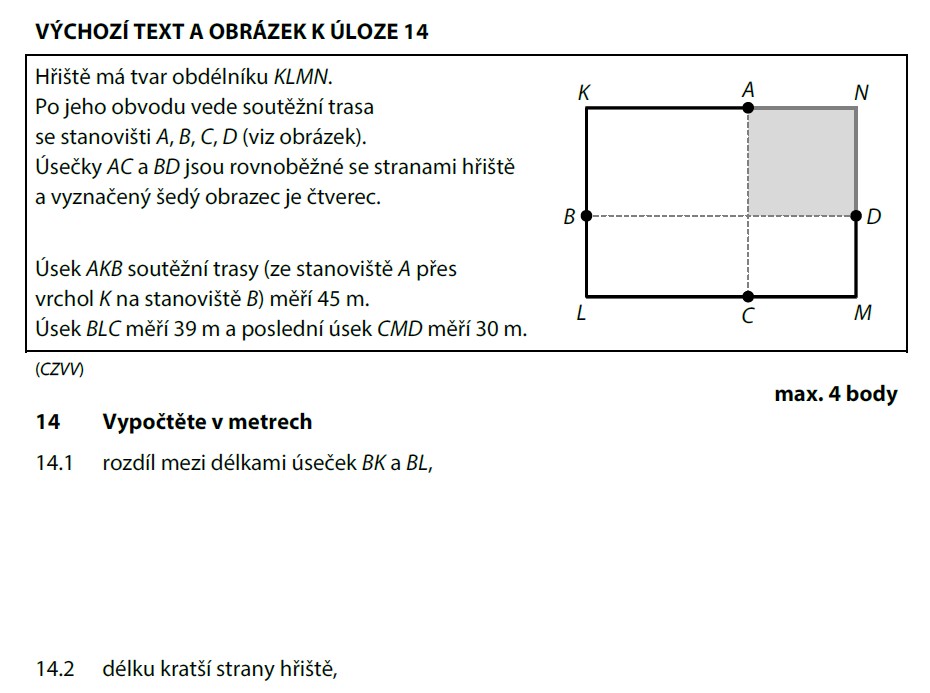
📋 Zadání — 2. náhradní termín, Úloha 14 (4 body)

Obdélníkové hřiště KLMN se stanovišti A, B, C, D a čtvercem uvnitř. Trasy: AKB = 45 m, BLC = 39 m, CMD = 30 m.

14.1) Rozdíl BK a BL?

14.2) Kratší strana hřiště?

14.3) Obvod hřiště?

14.4) Vzdálenost D od N?

1 Rozdíl BK a BL

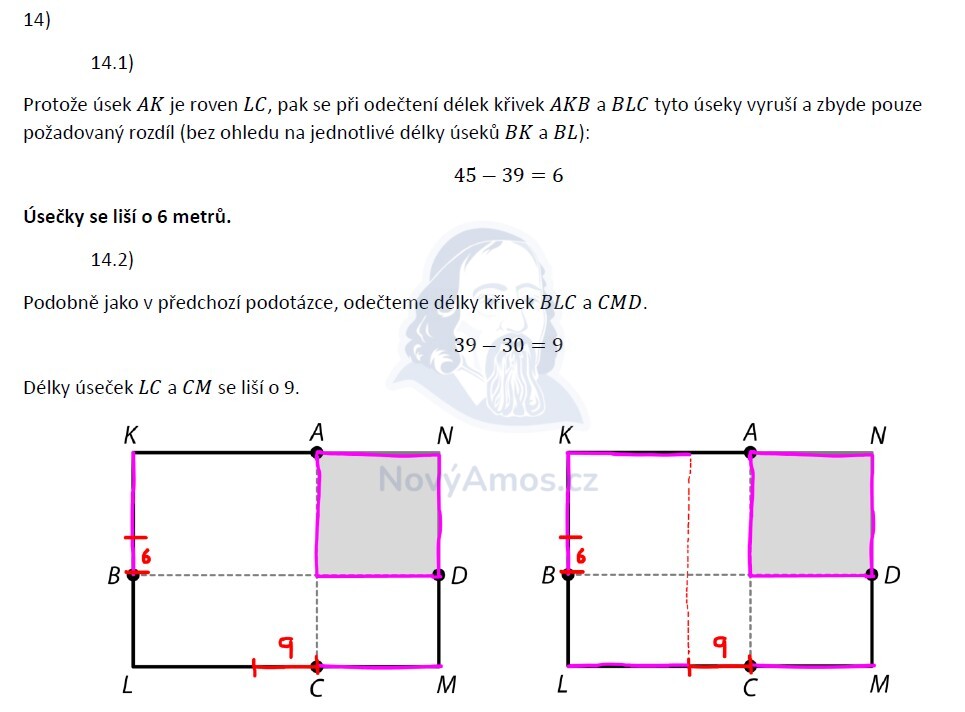
AK a LC jsou rovnoběžné úsečky (protilehlé strany obdélníku), takže jsou stejně dlouhé: AK = LC. Rozdíl tras tedy závisí jen na BK a BL:

Rozdíl BK a BL = 45 − 39 = 6 m

2 Strana čtverce a kratší strana hřiště

Stejně tak: LC − CM = rozdíl tras BLC a CMD:

39 − 30 = 9 m (LC − CM = BL − BK... ne, to je vzdálenost)

Z trasy AKB: strana čtverce = (45 − 9) : 2 = 18 m. BL = 39 − 9 − 18 = 12 m.

Kratší strana = BK + BL = 18 + 12 = 30 m

3 Obvod hřiště a vzdálenost DN

Sečteme všechny trasy a přidáme strany čtverce:

Obvod = 45 + 39 + 30 + 2 × 18 = 45 + 39 + 30 + 36 = 150 m

DN = strana čtverce (D leží na straně MN, vzdálenost k rohu N):

DN = 18 m

✅ Výsledek

14.1) 6 m 14.2) 30 m 14.3) 150 m 14.4) 18 m

💡 Tip pro CERMAT

Hledej, jaké úseky se opakují nebo jsou si rovny — rovnoběžné strany obdélníku jsou vždy stejně dlouhé. Když odečteš dvě trasy, zbydou ti přesně ty úseky, které se liší!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 11 (2 body)

Trojúhelník ABC a čtverec DEFG ve čtvercové síti (1 cm čtvereček). O kolik se liší obvod trojúhelníku ABC a obvod čtverce DEFG?

Výběrová úloha: A) o 2 cm, B) o 3 cm, C) o 3,5 cm, D) o 4 cm, E) o jiný počet cm

1 Spočítáme obvod čtverce

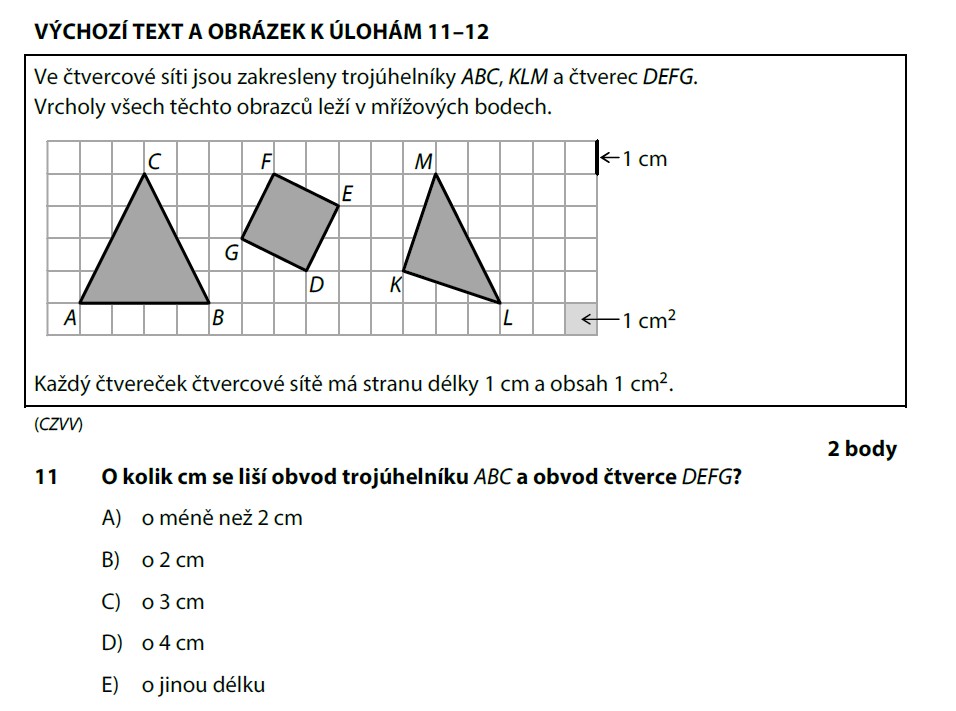
Čtverec DEFG ve čtvercové síti — odečteme délku strany z obrázku. Pokud strana = délka, obvod = 4 × strana.

Z obrázku odečteme strany a spočítáme obvody obou útvarů.

2 Porovnáme obvody

Obvod trojúhelníku ABC je o 4 cm delší než obvod čtverce DEFG.

Obvod ABC − Obvod DEFG = 4 cm

✅ Výsledek

D) o 4 cm

💡 Tip pro CERMAT

Ve čtvercové síti: vodorovné a svislé strany spočítáš snadno (počet čtverečků). U šikmých stran (úhlopříček) si spočítej, kolik čtverečků jdou do strany a kolik nahoru — šikmá strana bude vždy delší než delší z těchto dvou čísel!

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Obvody

Co si odnést z tohoto tématu

🧭 Strategie řešení

Obvod = délka cesty kolem celého tvaru — sečti všechny vnější strany
U složených tvarů najdi základní jednotku (stranu trojúhelníku, čtverečku) a počítej, kolikrát se opakuje
Obvod obdélníku = 2 × (délka + šířka) — součet sousedních stran = obvod : 2
U obdélníků se stejným obvodem hledej všechny dvojice celých čísel dávající tento součet

⚠️ Typické chytáky

Lomená čára podél čtverečků má STEJNOU délku jako obvod obdélníku — rovnoběžné odskoky se vyruší!
Rozestupy vs. body: N rozestupů = N+1 bodů (květin, stromků...) — nezapomeň přičíst rohový bod!
Při přeskládání se mění obvod, i když obsah zůstane stejný
Pozor na převod jednotek: metry vs. centimetry u rozestupů

❌ Nejčastější chyby

Zapomenout, že „o čtvrtinu menší" = poměr 4 : 3 (dílky!)
Při stejném obvodu: čím blíže ke čtverci, tím větší obsah — ale CERMAT se ptá na obvod, ne obsah!
Nepřevést jednotky (metry a centimetry) na stejné před počítáním

📐 Obvody — jednoduché i složité tvary

🔑 Co je obvod?

🎯 Rady pro CERMAT: Obvody