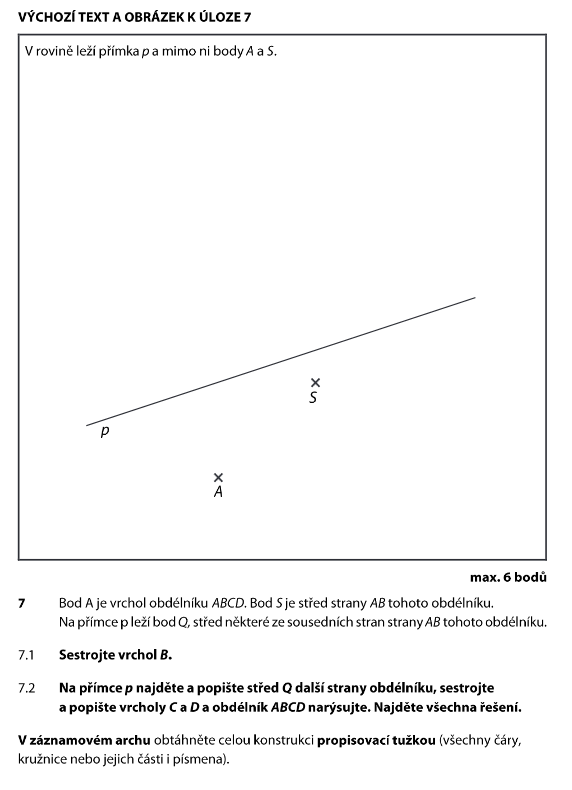
S je střed strany AB. To znamená, že A a B jsou od S stejně daleko, ale na opačných stranách.
- Změříme kružítkem vzdálenost |SA|
- Narýsujeme kružnici se středem S a poloměrem |SA|
- Bod B leží na kružnici — na opačné straně od A (přes střed S)
Jednodušeji: od bodu S naměříme vzdálenost |SA| na druhou stranu a máme bod B!
Teď máme oba body A i B. Spojíme je a dostaneme přímku AB — to je jedna strana obdélníku.
Obdélník má protější strany rovnoběžné a všechny úhly pravé (90°). Sousední strana s AB musí být na ni kolmá!
Q je střed sousední strany k AB — to je strana AD nebo BC. Sousední strana je kolmá na AB.
- Q leží na přímce p
- Q leží na kolmici k přímce AB (protože sousední strana je kolmá na AB)
- Q najdeme jako průsečík přímky p s kolmicí vedenou z vhodného bodu
Q je střed sousední strany. Pokud je to střed strany AD:
- |AQ| = |QD| → D najdeme kružnicí se středem Q, poloměr |AQ|
- Z bodu D vedeme rovnoběžku s AB → na ní leží bod C
- Z bodu B vedeme kolmici k AB → průsečík s rovnoběžkou = bod C
Spojíme A-B-C-D a máme obdélník!
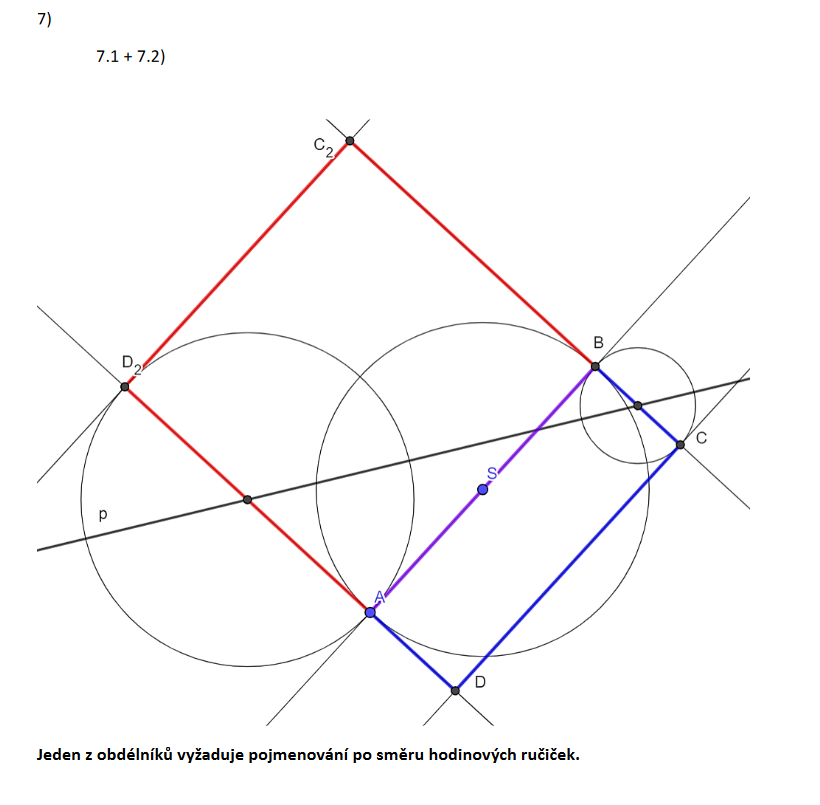
Obdélník může ležet na dvou stranách od přímky AB:
- 1. řešení: body C a D na jedné straně od AB
- 2. řešení: body C a D na druhé straně od AB
CERMAT chce obě řešení! Nezapomeň narýsovat oba obdélníky.
Když je bod S střed úsečky AB, tak:
- Narýsuješ kružnici se středem S a poloměrem |SA|
- Bod B je na opačné straně — je to jako „zrcadlo" přes bod S
- Tomuhle se říká souměrnost podle středu a CERMAT to miluje!

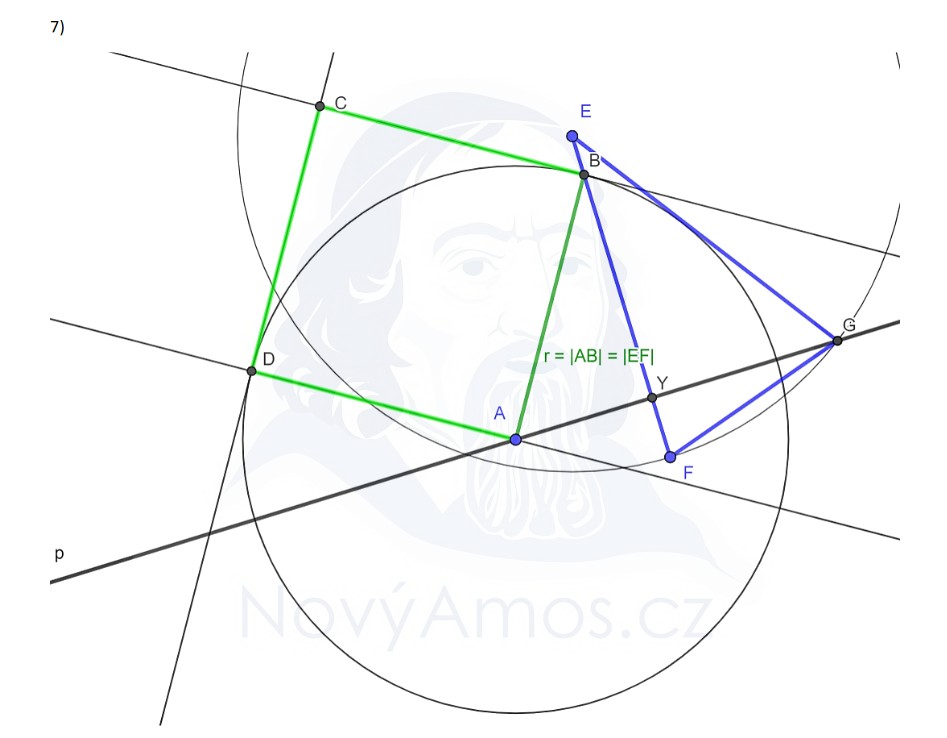
Začneme tím, co je v zadání:
- Spojíme body E a F → úsečka EF
- Z bodu A sestrojíme kolmici k úsečce EF (pomocí trojúhelníku s pravítkem)
- Kolmice protne EF v bodě Y — to je průsečík!
Teď máme přímku p (kolmici) a bod Y. Skvělý začátek!
Potřebujeme bod B na EF tak, aby |AB| = |YE|.
- Kružítkem změříme vzdálenost |YE|
- Narýsujeme kružnici se středem A a poloměrem |YE|
- Průsečík kružnice s úsečkou EF je bod B
Kružnice může protnout EF ve dvou bodech — vybereme ten správný podle dalších podmínek.
Čtverec má všechny strany stejně dlouhé a všechny úhly pravé (90°).
- Známe stranu AB → délka strany čtverce = |AB|
- Z bodu A vedeme kolmici k AB → na ní leží bod D
- Na kolmici naměříme |AB| → bod D
- Z D vedeme rovnoběžku s AB, z B kolmici k AB → průsečík = bod C
- Podmínka: Y neleží uvnitř čtverce — to nám řekne, na kterou stranu od AB čtverec narýsovat
Ramena trojúhelníku FGE jsou EF a EG. To znamená: |EF| = |EG| (jsou to ramena).
- Kružítkem změříme |EF|
- Narýsujeme kružnici se středem E a poloměrem |EF|
- Bod G leží na polopřímce AY — najdeme průsečík kružnice s touto polopřímkou
- Spojíme F, G, E → rovnoramenný trojúhelník!
Tato úloha má hodně kroků — neboj se, dělej je postupně:
- Každý krok závisí na předchozím, takže je řeš popořadě
- Kolmice = trojúhelník s pravítkem, přenos vzdálenosti = kružítko
- Podmínka „Y neleží uvnitř" ti řekne, na kterou stranu rýsovat čtverec
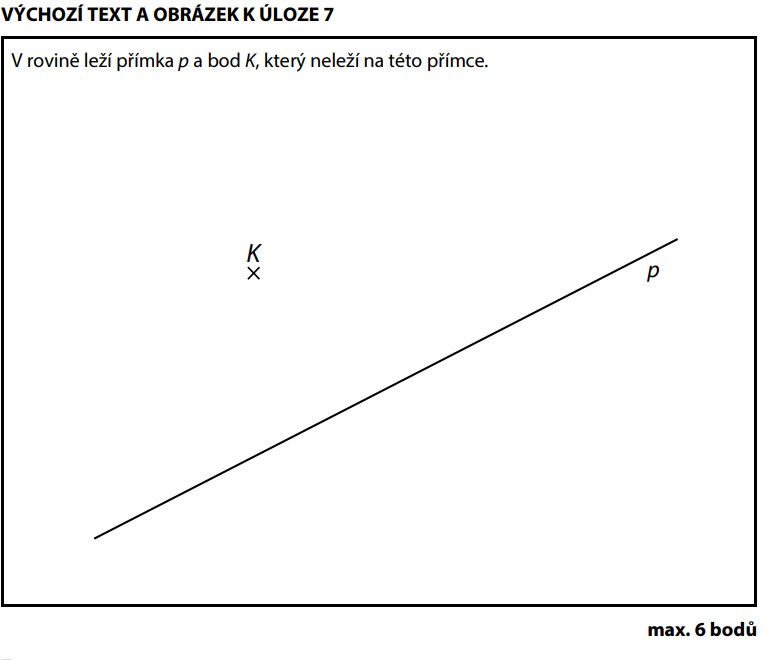
L a M leží na přímce p a KLMN je čtverec. Strana KL musí být kolmá na přímku p (protože LM leží na p a v čtverci je úhel 90°).
- Z bodu K sestrojíme kolmici na přímku p
- Kolmice protne přímku p v bodě — to je bod L (pata kolmice)
Čtverec má všechny strany stejně dlouhé. Délka strany = |KL|.
- Kružítkem změříme vzdálenost |KL|
- Narýsujeme kružnici se středem L a poloměrem |KL|
- Průsečík kružnice s přímkou p je bod M
Pozor: kružnice protne přímku p ve dvou bodech — M může být vlevo i vpravo od L!
Máme K, L, M — chybí nám bod N.
- Z bodu M vedeme kolmici k přímce p (strana MN je kolmá na LM)
- Na kolmici naměříme |KL| → bod N
- Nebo: z K vedeme rovnoběžku s p, z M kolmici k p → průsečík = N
- Spojíme K-L-M-N → čtverec!
Ramena trojúhelníku jsou KM a KZ → |KM| = |KZ|.
- Kružítkem změříme vzdálenost |KM| (úhlopříčka čtverce)
- Narýsujeme kružnici se středem K a poloměrem |KM|
- Bod Z leží na přímce p → najdeme průsečík kružnice s přímkou p
- Spojíme K, Z, M → rovnoramenný trojúhelník!
Zkontrolujeme si:
- Je KLMN opravdu čtverec? (Všechny strany stejné, úhly 90°) ✅
- Leží L a M na přímce p? ✅
- Je |KM| = |KZ|? (Oba jsou na kružnici se středem K) ✅
- Leží Z na přímce p? ✅
Existují 2 řešení — M může být na obou stranách od L.
U čtverce si pamatuj tři klíčové kroky:
- Kolmice — strany čtverce na sebe kolmé (úhel 90°)
- Kružnice — přenos délky strany (všechny strany stejné)
- Dvě řešení — kružnice protne přímku ve dvou bodech!


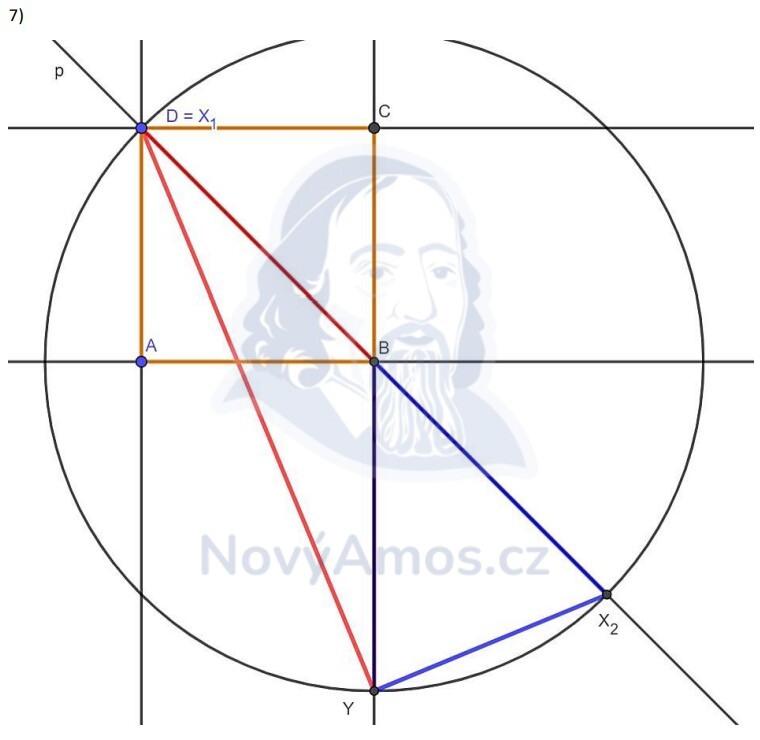
Máme body A, C, D. Trojúhelník ACD je rovnoramenný pravoúhlý (pravý úhel při D, ramena AD a DC).
- |AD| = |DC| (rovnoramenný) a úhel ADC = 90°
- Čtverec ABCD: strany AB, BC, CD, DA — bod B je čtvrtý vrchol
- AC je úhlopříčka čtverce — bod B doplníme „na druhou stranu"
- Z bodu A vedeme rovnoběžku s DC, z bodu C rovnoběžku s DA → průsečík = bod B
Přímka p prochází body B a D — to je úhlopříčka čtverce BD.
- Spojíme B a D → přímka p
- Potřebujeme bod X na přímce p, kde |BX| = |BD|
- Narýsujeme kružnici se středem B a poloměrem |BD|
- Kružnice protne přímku p ve dvou bodech!
Jeden průsečík je přímo bod D (protože |BD| = |BD|). Druhý bod X leží na opačné straně od B.
|BY| = |BX| = |BD|. Bod Y leží na polopřímce CB (začíná v C a pokračuje přes B dál).
- Kružnici se středem B a poloměrem |BD| už máme narýsovanou
- Najdeme průsečík kružnice s polopřímkou CB → bod Y
- |BY| = |BD| ✅
Teď spojíme body X, Y, B a máme trojúhelník!
Ale pozor — bod X může být na dvou místech (dva průsečíky kružnice s přímkou p):
- X₁ = D — jeden průsečík je přímo bod D
- X₂ — na opačné straně od D (přes B)
Proto existují 2 řešení — dva různé trojúhelníky XYB!
Hodně dětí zapomene, že kružnice protne přímku ve dvou bodech:
- Jeden bod X je přímo D (což je „triviální" řešení)
- Druhý bod X je na opačné straně — na ten se nesmí zapomenout!
- Vždy napiš: „Úloha má 2 řešení" — za to jsou body!
🎯 Rady pro CERMAT: Geometrické konstrukce
Co si odnést z tohoto tématu
- Vždy začni tím, co znáš — dané body, přímky, vzdálenosti
- Kolmice a kružnice jsou tvoje hlavní nástroje!
- Kolmice = pravoúhlý trojúhelník s pravítkem (úhel 90°)
- Kružnice = přenos vzdálenosti (kružítko)
- Hledej VŠECHNA řešení — většinou existují 2!
- Zapomenutí na druhé řešení — kružnice protne přímku většinou ve dvou bodech!
- Nepřesná konstrukce kružítkem — tužku nesmíš při rýsování naklánět
- Pozor na pořadí písmen ABCD — po směru nebo proti směru hodinových ručiček
- Střed úsečky = bod, odkud je stejná vzdálenost k oběma koncům
- Zapomenout narýsovat kružnice — CERMAT je chce vidět v obrázku!
- Neoznačit všechny body — každý bod musí mít své písmenko
- Zapomenout obtáhnout propiskou — rýsovat se musí propiskou, ne tužkou
- Nezapsat postup konstrukce: Dáno → Postup → Závěr (počet řešení)