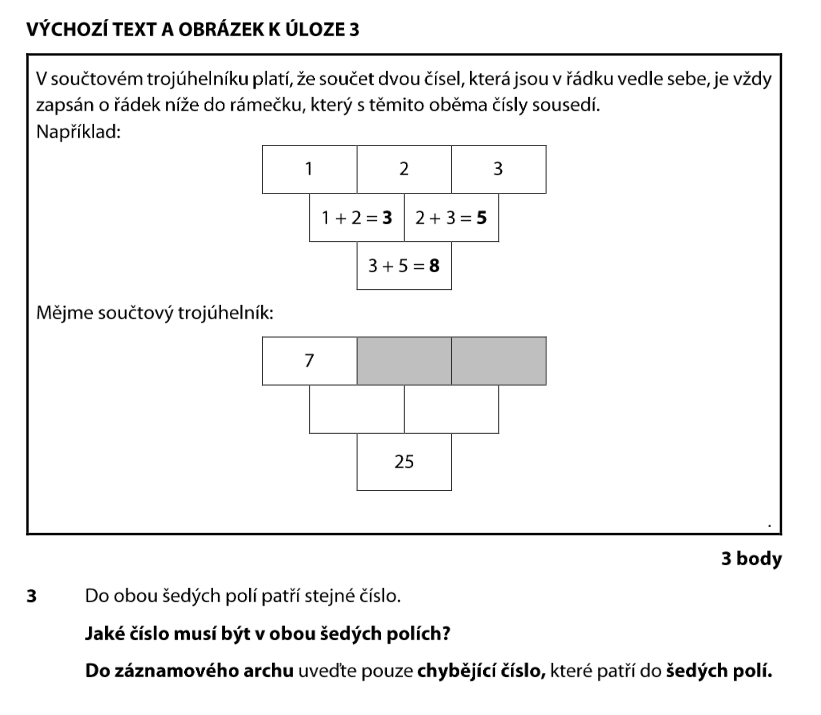
Pojďme si nejdřív připomenout pravidlo. Nahoře jsou tři čísla. Pod každou dvojicí sousedů je jejich součet:
1 + 2 = 3, potom 2 + 3 = 5, a nakonec 3 + 5 = 8.
Nahoře máme: 7, neznámé číslo (říkejme mu x), a zase x.
Druhý řádek: 7 + x a x + x (to je dvakrát x).
Třetí řádek (dole): součet druhého řádku = (7 + x) + (x + x) = 25.
Sečteme všechno, co je dole:
Takže výsledné číslo 25 obsahuje jedničku 7 a trojnásobek neznámého čísla. To je klíčový trik!
Nejdřív odečteme 7 od obou stran:
Teď víme, že trojnásobek neznámého čísla je 18. Vydělíme třemi:
Ověříme si to! Trojúhelník s šestkami:
7 + 6 = 13, 6 + 6 = 12, a 13 + 12 = 25. Sedí!
U součtového trojúhelníku se 3 čísly nahoře platí kouzelný vzorec:
- Dolní číslo = 1. číslo + 3 × prostřední + poslední číslo... ne, tady je to jednodušší!
- Když jsou dvě čísla stejná (šedá), dolní výsledek = známé číslo + 3 × neznámé
- Vždy si ověř dosazením — spočítej trojúhelník znovu s nalezeným číslem

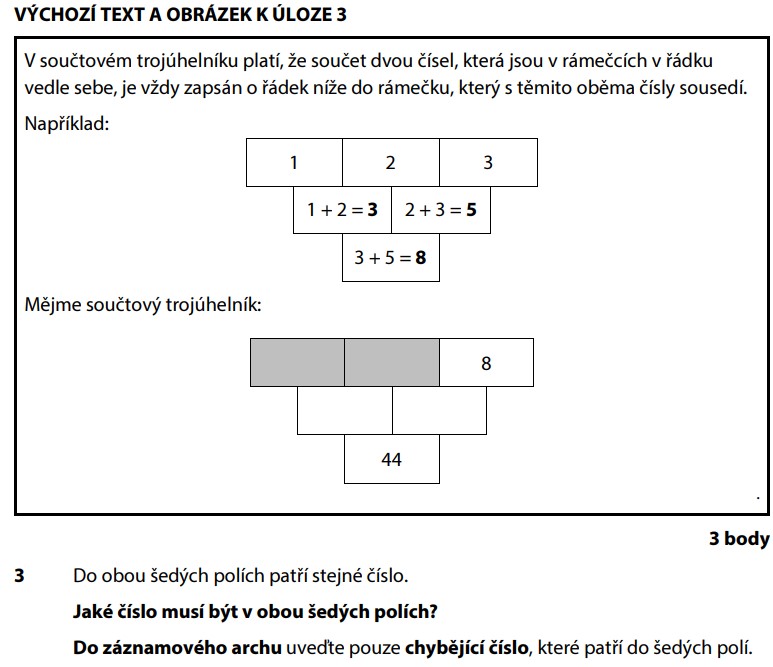
Tentokrát jsou šedá pole na začátku a známé číslo 8 je na konci:
Druhý řádek: x + x (dvakrát x) a x + 8.
Dole je součet druhého řádku:
A to se rovná 44. Takže:
Odečteme 8:
Vydělíme třemi:
Ověříme:
12 + 12 = 24, 12 + 8 = 20, a 24 + 20 = 44. Sedí!
Všimni si: tohle je stejný typ úlohy jako v prvním termínu! CERMAT miluje opakování. Vzorec je pokaždé stejný:
- Dolní číslo = 3 × neznámé + známé (nebo obráceně: známé + 3 × neznámé)
- Nezáleží, jestli je známé číslo vlevo nebo vpravo — trojnásobek neznámého je tam vždy
- Jde o to, že neznámé se objeví v dolním čísle přesně třikrát

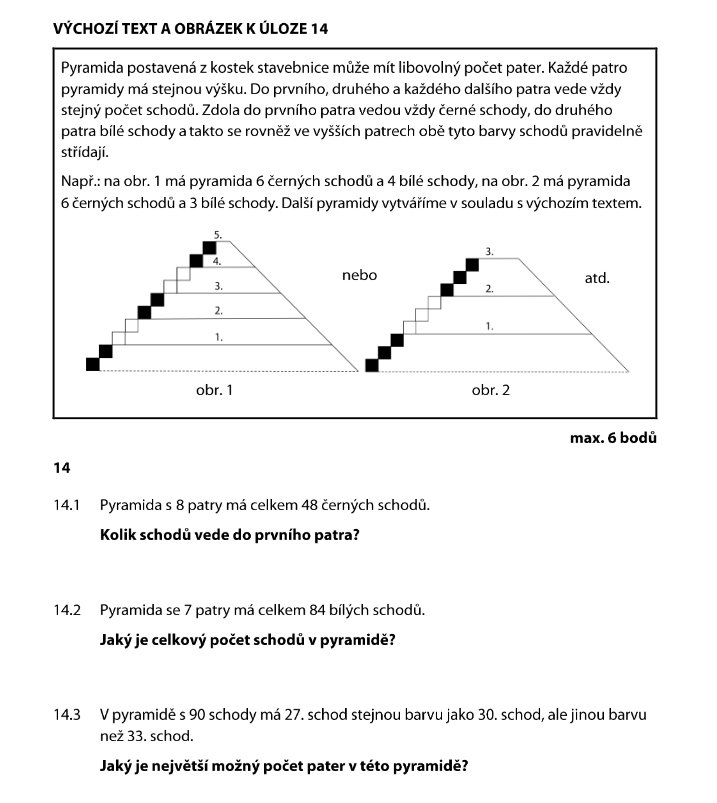
Máme 8 pater. Barvy se střídají: černé, bílé, černé, bílé...
8 pater = 4 černá (1., 3., 5., 7.) + 4 bílá (2., 4., 6., 8.). Sudý počet pater = stejně černých i bílých!
48 černých schodů patří do 4 černých pater. Ale kolik je schodů celkem? Černých i bílých je stejně:
96 schodů se rovnoměrně rozdělí do 8 pater (do každého stejný počet):
Do prvního patra vede 12 schodů.
7 pater je lichý počet. Barvy: černé, bílé, černé, bílé, černé, bílé, černé.
4 černá patra + 3 bílá patra. Poměr černých a bílých je 4 : 3.
84 bílých schodů patří do 3 bílých pater. Kolik schodů do jednoho patra?
Celkový počet schodů:
Podmínka: 27. a 30. schod mají stejnou barvu, ale 33. schod má barvu jinou.
To znamená, že 27. a 30. schod jsou ve stejném patře, ale 33. schod je už v dalším patře (jiné barvy).
Mezi 27. a 30. schodem jsou 3 schody (27, 28, 29, 30) — to ještě nevíme, jestli patří do jednoho patra. Ale hranice pater musí být někde mezi 30. a 33. schodem.
Abychom měli co nejvíc pater, chceme co nejméně schodů na patro. Nejméně schodů, při kterých 27. a 30. spadnou do jednoho patra a 33. do dalšího, je 5 schodů na patro:
Ověřme: 27. a 30. schod jsou oba v patře 26–30 (stejná barva). 33. schod je v patře 31–35 (jiná barva). Sedí!
U pyramidy se střídajícími barvami:
- Sudý počet pater = stejně černých i bílých (poměr 1 : 1)
- Lichý počet pater = o jedno více černých (poměr n+1 : n)
- U 14.3: chceš nejvíc pater = co nejméně schodů na patro. Zkus nejmenší počet, který splní podmínky!


Čteme pozorně: „každá třetí slepice" = každá 3. z celkových 99.
Zbývá 99 − 33 = 66 slepic. Z nich „každá druhá":
Ale pozor! Oficiální řešení počítá jinak: „každá druhá" ze všech 99 slepic = 99 : 2 = 49 (zaokrouhlíme dolů). Pak odečteme ty, co už snášejí denně:
A zbytek:
Spočítáme, kolik vajíček snese každá skupina za 6 dní:
| Skupina | Počet slepic | Jak často | Vajíčka za 6 dní |
|---|---|---|---|
| Denní 🟢 | 33 | každý den (6×) | 33 × 6 = 198 |
| Každý 2. den 🔵 | 16 | každý 2. den (3×) | 16 × 3 = 48 |
| Každý 3. den 🟡 | 50 | každý 3. den (2×) | 50 × 2 = 100 |
| Celkem za 6 dní | 198 + 48 + 100 = 346 | ||
Všimni si: 6 dní je společný cyklus pro všechny skupiny (denní, každý 2. den, každý 3. den). Za každých 6 dní se vzorec opakuje!
Celkem vajíček za 30 dní:
Jedno vajíčko = 3 Kč:
42 dní = kolik šestidenních cyklů?
Vajíčka za 42 dní:
Tržba za vajíčka:
Plus prodej slepic za 6 000 Kč:
Pozor na rozdělení slepic! „Každá třetí" neznamená totéž co „třetina zbylých".
- „Každá třetí slepice" = 99 : 3 = 33 slepic
- „Každá druhá ze zbývajících" — tady si dej pozor: oficiální řešení bere „každou druhou" ze všech 99 = 49, a pak odečte ty, co už snášejí denně (49 − 33 = 16)
- Klíčový trik: cyklus 6 dní. Čísla 1, 2 a 3 mají společný násobek 6. Stačí spočítat jeden cyklus a pak násobit!


🎯 Rady pro CERMAT: Vzory a posloupnosti
Co si odnést z tohoto tématu
- U součtových trojúhelníků: vyjádři dolní číslo pomocí známých a neznámých. Neznámé se vždy objeví třikrát
- U schodů/pyramidy: zjisti, kolik pater je černých a kolik bílých (sudý počet pater = stejně, lichý = o jedno víc)
- U cyklických úloh: najdi délku cyklu (společný násobek), spočítej jeden cyklus a pak násobením celkový počet
- U „největšího počtu pater": chceš co nejméně schodů na patro — zkoušej od nejmenšího počtu
- U pyramidy: sudý počet pater = stejně černých i bílých, lichý = o jedno více černých pater
- U slepic: „každá třetí" neznamí totéž co „třetina zbylých" — čti zadání přesně!
- 90 : 5 = 18 — vyjde to přesně, ale CERMAT očekává, že to ověříš podmínkami (27. a 30. schod ve stejném patře, 33. v dalším)
- Cyklus vajíček: 6 dní (= společný násobek 1, 2 a 3). Stačí spočítat jeden cyklus!
- Špatný poměr černých a bílých pater (zapomenout, že lichý počet pater = nerovný poměr)
- U slepic: špatný počet skupin — pozorně přečti, jak se slepice dělí
- Zapomenutí na cyklus — počítat den po dni místo hledání opakujícího se vzorce
- U trojúhelníku: zapomenout ověřit výsledek dosazením zpátky