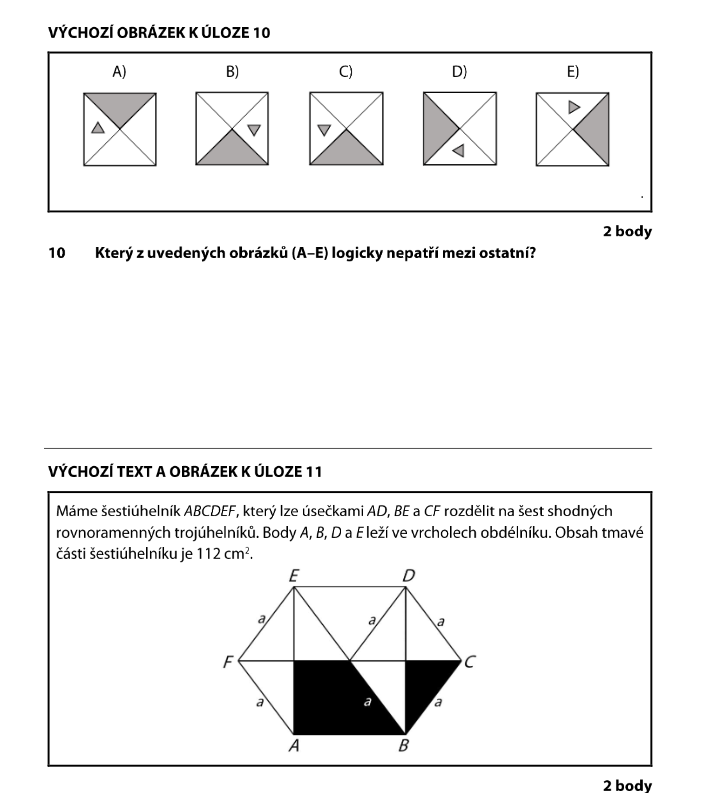
Všechny čtverce jsou rozdělené úhlopříčkami na 4 trojúhelníky. Některé trojúhelníky jsou bílé, jiné šedé a jiné černé.
Zkus si všimnout: dají se některé obrázky získat otočením jiného?
Vezmeme obrázek A a otáčíme ho:
- Otočíme o 90° → získáme jiný ze čtverců
- Otočíme o 180° → získáme další
- Otočíme o 270° → získáme další
Takto se dá získat většina obrázků otáčením — kromě jednoho!
Čtverec C nejde získat otáčením žádného z ostatních. Abychom získali C, museli bychom obrázek překlopit (zrcadlit) — jako bychom se dívali do zrcadla.
Rotací = otáčením v rovině získáme A, B, D, E navzájem. Ale C vyžaduje zrcadlení — a to je jiná operace!
Zkus si obrázky otáčet v hlavě o 90° — co jde otočit, je stejné. Co se musí převrátit (zrcadlit), nepatří!
- Rotace = otáčíš a vzor zůstává stejný
- Zrcadlení = překlápíš a vzor se změní (levá/pravá strana)

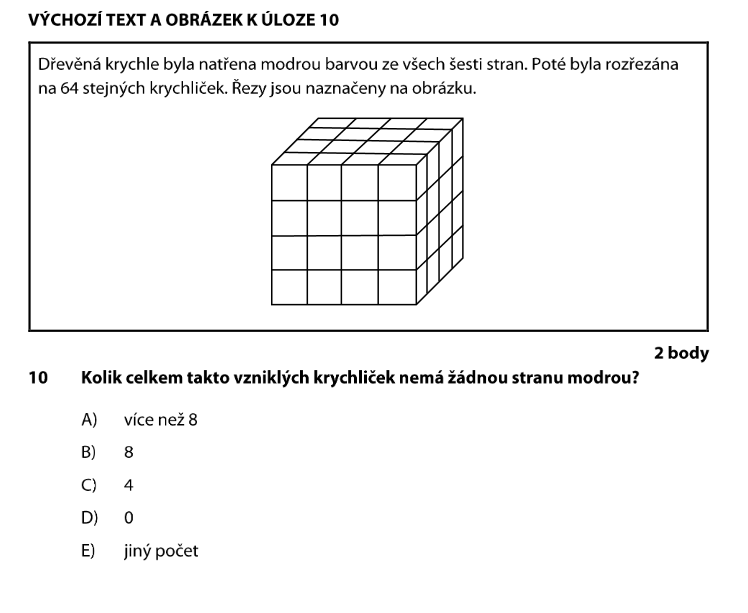
Máme krychli 4×4×4. Celá je natřená modře. Když ji rozřežeme, získáme 64 maličkých krychliček.
Některé krychličky jsou na povrchu (mají modrou barvu), jiné jsou schované uvnitř a nemají žádnou modrou stranu.
Schované krychličky = ty, které se nedotýkají povrchu velké krychle. Jsou úplně uvnitř.
Představ si to jako krabici čokoládových bonbónů. Povrchové bonbóny mají obal (modří barvu). Ty uvnitř žádný obal nemají.
Vnitřní krychličky tvoří menší krychli uvnitř. Stačí z každé strany „oloupit" jednu vrstvu:
Odečteme 2, protože z každé strany odstraníme jednu vrstvu (levá + pravá, horní + spodní, přední + zadní).
Tohle je klasická „Cermatovina"! Zapamatuj si vzorec:
- Krychle 3×3×3: (3−2)³ = 1³ = 1 krychlička uvnitř
- Krychle 4×4×4: (4−2)³ = 2³ = 8 krychliček uvnitř
- Krychle 5×5×5: (5−2)³ = 3³ = 27 krychliček uvnitř
Pozor: 4×4×4 má uvnitř 2×2×2, ne 3×3×3!

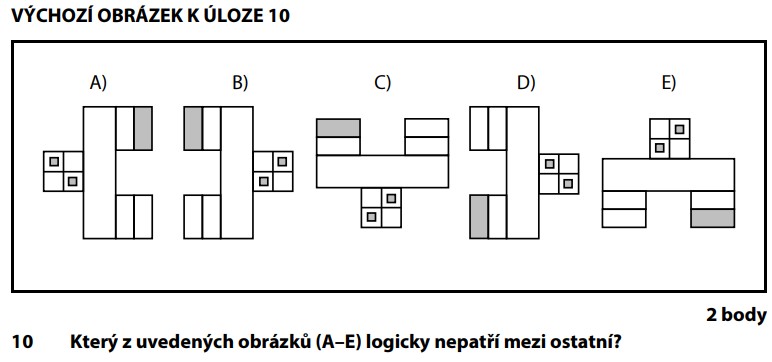
Všech 5 útvarů vypadá podobně — jsou složené ze stejných částí. Ale jeden z nich se od ostatních liší.
Zkusíme je otáčet v rovině (o 90°, 180°, 270°) a podíváme se, jestli z jednoho útvaru získáme ostatní.
Když vezmeme útvar A a otáčíme:
- A otočené o 90° → získáme C
- A otočené o 180° → získáme D
- A otočené o 270° → získáme E
Útvary A, C, D, E jsou vzájemné rotace. Ale co B?
Útvar B nezískáme otáčením žádného z ostatních v rovině. Museli bychom ho zrcadlit — a to je jiná operace než rotace!
Ostatní 4 útvary (A, C, D, E) jsou jen otočené verze jednoho a toho samého tvaru.
- Vždy si vyzkoušej všechny otáčky: 90°, 180°, 270°.
- Pokud útvar nejde získat žádnou rotací, nepatří mezi ostatní.
- Pozor: zrcadlení (překlápění) není to samé jako rotace (otáčení)!

🎯 Rady pro CERMAT: Prostorová představivost
Co si odnést z tohoto tématu
- U rotací: otáčej obrázek v hlavě o 90°, 180°, 270°
- U krychle: vnitřní kostky spočti jako (n−2)³
- Zkus si to nakreslit — nákres pomůže víc než přemýšlení
- U útvarů: nejdřív zkus otáčení v rovině, teprve pak překlápění
- Záměna rotace a zrcadlení — rotací zachováš orientaci, zrcadlením ne!
- U krychlí zapomenutí na schované kostky uvnitř
- Pozor: krychle 4×4×4 má uvnitř 2×2×2, ne 3×3×3!
- Při porovnávání obrázků se nenech zmást podobností — vždy otoč všemi směry
- Otočit obrázek jen v hlavě a nezkontrolovat všechny směry
- Spočítat povrchové kostky místo vnitřních
- Myslet si, že zrcadlový obraz je to samé jako otočený