Čtení grafů a A/N tvrzení

📋 Zadání — 1. řádný termín, Úloha 12 (3 body)

Sloupcový graf ukazuje přírůstky a úbytky obyvatel v obcích Lidov, Dámov a Pánov v letech 2019–2022. Kladné hodnoty = přírůstek, záporné = úbytek.

Rok	Lidov	Dámov	Pánov
2019	+10	−5	−10
2020	+5	−10	+5
2021	−5	+10	+10
2022	+10	+5	−5

12.1) Jak se změnil počet obyvatel v Pánově během roku 2021?

12.2) Lidov měl 1. 1. 2019 právě 300 obyvatel. Kolik měl po třech letech (31. 12. 2021)?

12.3) Jak se změnil počet obyvatel v Dámově za všechny 4 roky dohromady?

1 Přečteme graf — co znamenají sloupce?

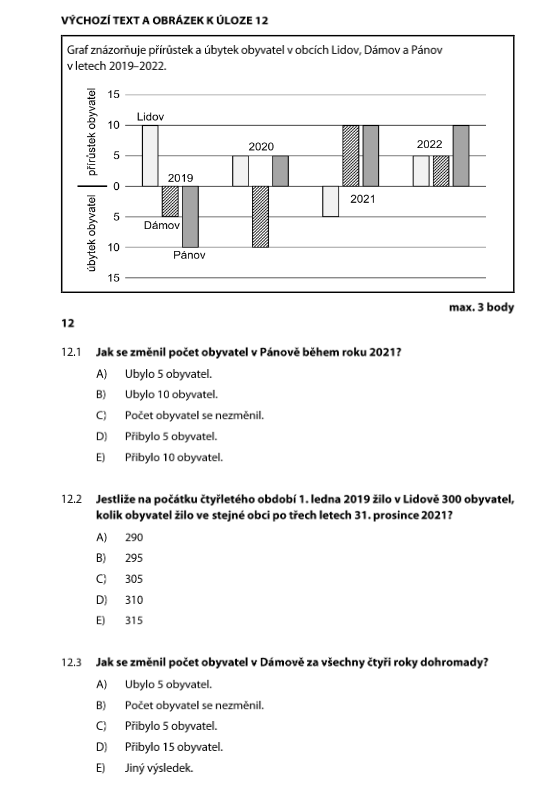
V grafu jsou kladné sloupce (nad nulou) a záporné sloupce (pod nulou):

Kladné = přibylo obyvatel
Záporné = ubylo obyvatel

Teď se podíváme na každou otázku zvlášť.

2 12.1: Pánov v roce 2021

Najdeme v tabulce řádek 2021 a sloupec Pánov:

Pánov 2021 = +10

V roce 2021 přibylo v Pánově 10 obyvatel.

Odpověď: E) Přibylo 10 obyvatel E

3 12.2: Kolik měl Lidov 31. 12. 2021?

Lidov měl na začátku roku 2019 přesně 300 obyvatel. Musíme přičíst změny za roky 2019, 2020 a 2021:

300 + (+10) + (+5) + (−5)

Počítáme postupně:

300 + 10 = 310, 310 + 5 = 315, 315 − 5 = 310

Odpověď: D) 310 obyvatel D

4 12.3: Dámov za všechny 4 roky

Sečteme změny v Dámově za roky 2019–2022:

(−5) + (−10) + (+10) + (+5)

−5 − 10 + 10 + 5 = 0

Celková změna je nula — počet obyvatel se za 4 roky nezmění!

Odpověď: B) Počet se nezměnil B

✅ Výsledek

12.1) E 12.2) D (310) 12.3) B

💡 Tip pro CERMAT

U grafů s přírůstky a úbytky si dej pozor:

Záporné hodnoty — nezapomeň je odečíst, ne přičíst!
Když sčítáš více let, jdi postupně rok po roku, ať neuděláš chybu.
Zkontroluj, zda se ptají na 1 rok nebo na součet za více let.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 8 (3 body)

Graf ukazuje, kolik hodin denně strávil Petr sportem, na počítači a učením během jednoho týdne.

Den	⚽ Sport	💻 Počítač	📚 Učení
Po	1	1,5	1
Út	0	1	1
St	2	2	2
Čt	2	2	2
Pá	3	3	0
So	0	1,5	1
Ne	0	1	0
Celkem	8 h	12 h	7 h

8.1) Na počítači strávil Petr o polovinu více času než sportem.

8.2) Učením strávil více času než sportem.

8.3) Aby strávil učením stejně času jako na počítači, musel by se učit o 5 hodin déle.

1 Sečteme hodiny za celý týden

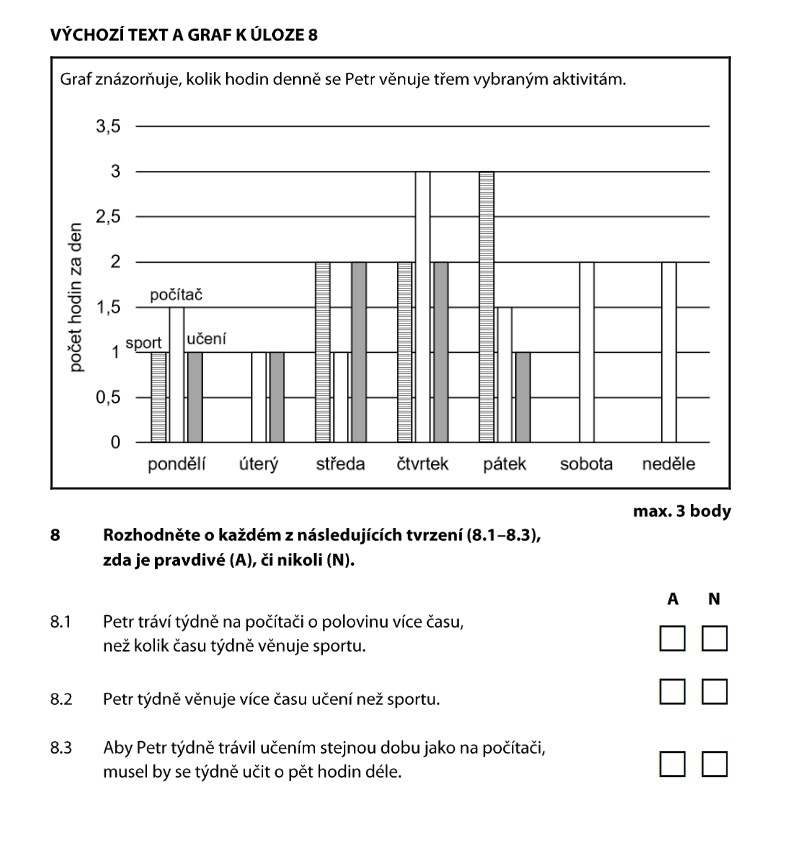
Z grafu odečteme hodiny pro každý den a sečteme za celý týden:

Činnost	Součet
⚽ Sport	8 hodin
💻 Počítač	12 hodin
📚 Učení	7 hodin

S těmito čísly ověříme všechna tři tvrzení.

2 8.1: "O polovinu více" na počítači než sport?

Sport = 8 h, počítač = 12 h.

"O polovinu více" znamená: vezmi sport (8) a přidej jeho polovinu:

8 : 2 = 4

8 + 4 = 12 ✅

8 + 4 = 12. A na počítači je přesně 12 hodin. Souhlasí! A — pravdivé

3 8.2 a 8.3: Ověříme zbytek

8.2: Učení = 7 h, sport = 8 h.

7 < 8

Učením strávil méně času než sportem, ne více. N — nepravdivé

8.3: Počítač = 12 h, učení = 7 h. Kolik hodin chybí?

12 − 7 = 5

Ano, musel by se učit o 5 hodin déle, aby to bylo 12. A — pravdivé

✅ Výsledek

8.1) A 8.2) N 8.3) A

⚠️ Pozor na chyták CERMATu

"O polovinu více" neznamená "dvakrát tolik"!

O polovinu více = původní + polovina z původního = 1,5 × původní
Dvakrát tolik = 2 × původní
Tady: 8 + 4 = 12 (o polovinu více). Dvakrát tolik by bylo 16!

📝 Oficiální řešení CERMAT

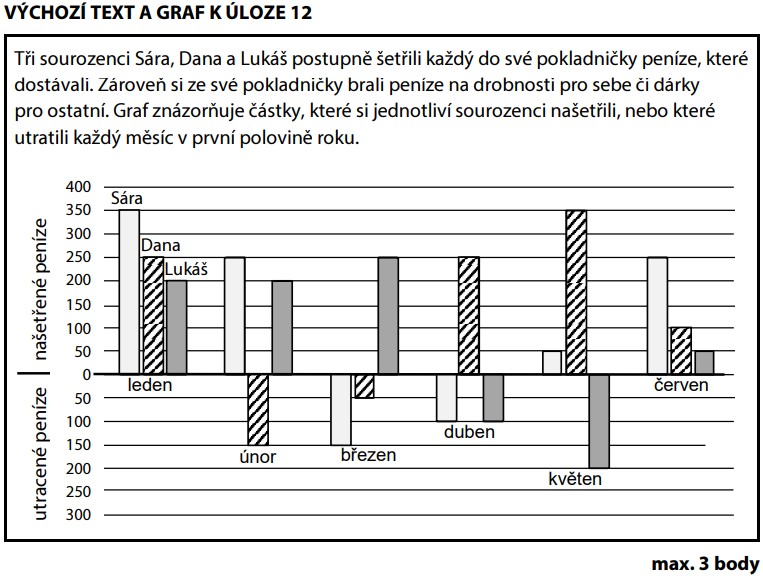
📋 Zadání — 1. náhradní termín, Úloha 12 (3 body)

Sourozenci Sára, Dana a Lukáš spoří. Graf ukazuje, kolik každý měsíc naspořili (+) a utratili (−) od ledna do června. Lukáš měl 1. ledna v pokladničce 600 Kč.

12.1) Kolik měl Lukáš na konci června?

12.2) O kolik se změnila částka Sáry za půl roku?

12.3) Kolik měli všichni dohromady na konci června? (Sára začínala s 1 050 Kč, Dana s 750 Kč)

1 Přečteme data z grafu

Z grafu pečlivě odečteme měsíční změny pro každého sourozence (kladné = naspořil, záporné = utratil):

Hodnoty musíme přečíst přesně z osy y. Každý sloupec nad nulou je přírůstek, pod nulou úbytek.

Teď se podíváme na každou otázku.

2 12.1: Kolik měl Lukáš na konci června?

Lukáš začínal s 600 Kč. K tomu přičteme všechny měsíční změny (leden až červen):

Sečteme přírůstky a úbytky z grafu. Podle oficiálního řešení:

600 + (změny leden–červen) = 1 000 Kč

Odpověď: D) 1 000 Kč D

3 12.2: Změna částky Sáry za půl roku

Sečteme všechny měsíční změny Sáry (leden–červen). Podle oficiálního řešení:

Celková změna Sáry = +650 Kč

Sára měla na konci června o 650 Kč více než na začátku ledna.

Odpověď: B) 650 Kč B

4 12.3: Kolik měli všichni dohromady?

Počáteční stavy: Sára = 1 050 Kč, Dana = 750 Kč, Lukáš = 600 Kč.

K počátečním stavům přičteme celkové změny za půl roku. Podle oficiálního řešení konečné stavy dohromady:

Sára + Dana + Lukáš = 4 200 Kč

Odpověď: E) 4 200 Kč E

✅ Výsledek

12.1) D (1 000 Kč) 12.2) B (650 Kč) 12.3) E (4 200 Kč)

💡 Tip pro CERMAT

U grafů se spořením a utrácením:

Nepřehlédni počáteční stav — výsledek není jen součet změn, ale počáteční stav + součet změn!
Záporné sloupce = útrata, nezapomeň je odečíst.
Když se ptají na změnu, nemusíš znát počáteční stav — stačí sečíst přírůstky a úbytky.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 13 (3 body)

Pepa sbíral za týden hrušky, jablka a hroznové víno. Celkový sběr:

Plodina	Celkem (kg)
🍎 Jablka	775 kg
🍐 Hrušky	750 kg
🍇 Hroznové víno	1 125 kg

13.1) Kdyby nasbíral o 25 kg jablek více, nasbíral by stejně jablek jako hrušek.

13.2) Nejvíce nasbíral hroznového vína.

13.3) Devítina hroznového vína se rovná šestině hrušek.

1 13.1: Jablka + 25 kg = hrušky?

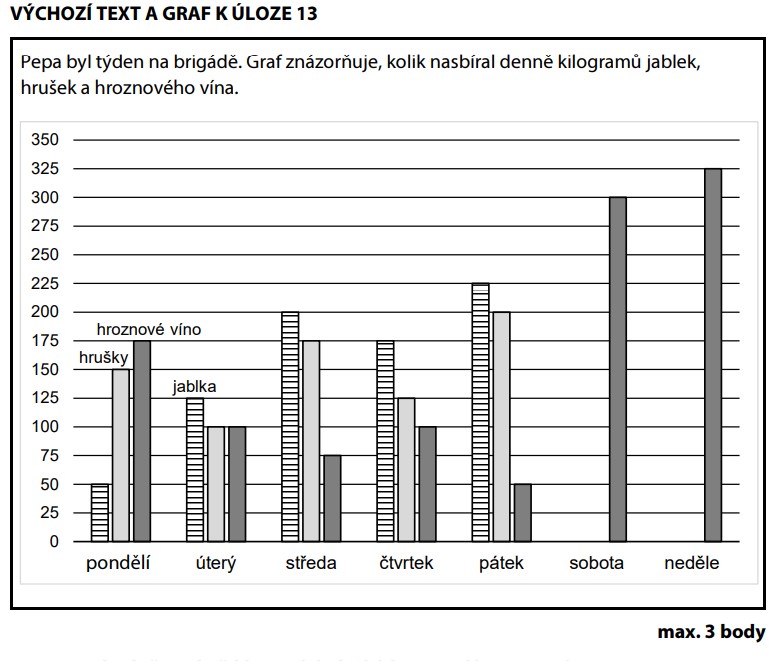
Jablka = 775 kg, hrušky = 750 kg. Tvrzení říká: kdyby přidal 25 kg jablek, bylo by jich stejně jako hrušek.

775 + 25 = 800

800 ≠ 750

800 kg jablek se nerovná 750 kg hrušek. Tvrzení je nepravdivé! N — nepravdivé

Pozor: kdyby měl o 25 kg méně jablek, pak by bylo 775 − 25 = 750 = hrušky. Ale tvrzení říká VÍCE!

2 13.2: Nejvíce nasbíral vína?

Porovnáme celkové kilogramy:

Jablka: 775 Hrušky: 750 Víno: 1 125

1 125 > 775 > 750 ✅

Ano, hroznového vína nasbíral nejvíce. A — pravdivé

3 13.3: Devítina vína = šestina hrušek?

Spočítáme obě strany:

1 125 : 9 = 125

750 : 6 = 125

125 = 125 ✅

Obě strany dají 125 kg. Souhlasí! A — pravdivé

✅ Výsledek

13.1) N 13.2) A 13.3) A

⚠️ Pozor na chyták CERMATu

Tvrzení 13.1 je typická past:

"O 25 kg více" neznamená "o 25 kg méně" — čti přesně, jestli tvrzení říká VÍCE nebo MÉNĚ!
U tvrzení 13.3 stačí vydělit a porovnat. Zlomek z čísla = číslo děleno jmenovatelem.
Vždy si spočítej obě strany tvrzení zvlášť a porovnej.

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Čtení grafů a A/N tvrzení

Co si odnést z tohoto tématu

🧭 Strategie řešení

Sečti hodnoty za celé období — jdi rok po roku, ať se nespletneš
Přesně odečítej z osy — záporné hodnoty jsou pod nulou!
U zlomků (1/9 z jednoho = 1/6 z druhého): spočítej obě strany zvlášť a porovnej
Zkontroluj, na co se ptají: změna (jen součet) vs. konečný stav (počáteční + součet)

⚠️ Typické chytáky

"O polovinu více" = 1,5 × původní, ne 2 × původní!
Záporné hodnoty v grafu = úbytek — musíš je odečíst, ne přičíst
"O 25 kg více" neznamená "o 25 kg méně" — čti pečlivě směr!
Nepřehlédni počáteční stav — konečný stav = začátek + změny

❌ Nejčastější chyby

Nepřesné čtení z grafu — dívej se na osu, neodhaduj výšku sloupce
Zapomenutí na záporné hodnoty — sečteš jen kladné a výsledek je moc velký
Špatné sčítání kladných a záporných čísel — postupuj po jednom a kontroluj

📊 Čtení grafů a A/N tvrzení

🔑 Jak číst grafy a rozhodovat A/N

🎯 Rady pro CERMAT: Čtení grafů a A/N tvrzení