Obsahy ve čtvercové síti

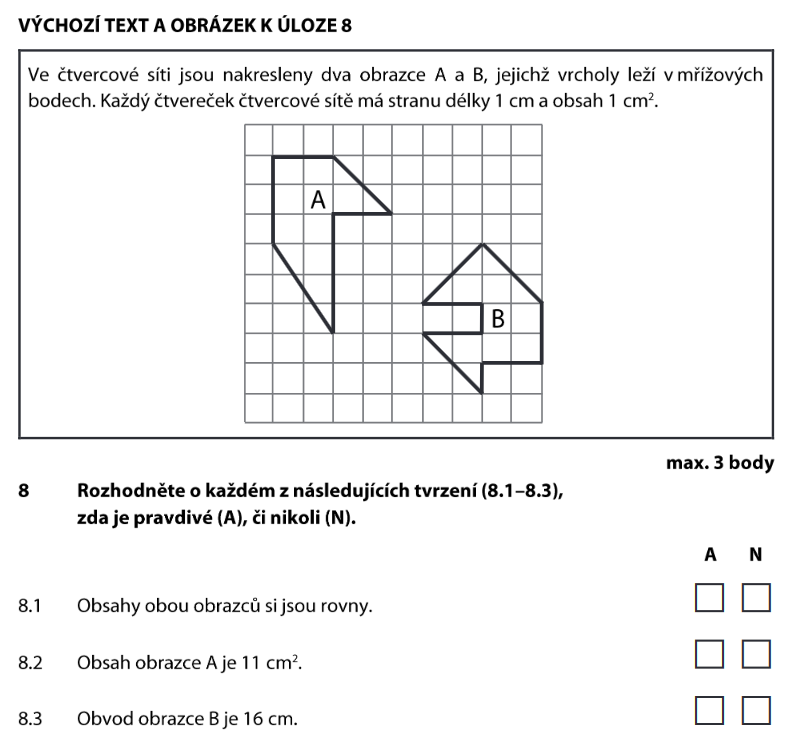
📋 Zadání — 1. řádný termín, Úloha 8 (3 body)

Ve čtvercové síti jsou dva obrazce A a B (strana čtverečku je 1 cm). Rozhodni, jestli platí (A), nebo neplatí (N):

8.1) Obsahy obou obrazců si jsou rovny.

8.2) Obsah obrazce A je 11 cm².

8.3) Obvod obrazce B je 16 cm.

1 Spočítáme obsah obrazce A

Obrazec A má složitý tvar. Rozložíme ho na jednodušší kousky — obdélníky a trojúhelníky — a jejich obsahy sečteme:

Kousek	Výpočet	Obsah
Obdélníková část	počítáme čtverečky	6 cm²
Trojúhelník 1	základna × výška : 2	3 cm²
Trojúhelník 2	základna × výška : 2	2 cm²
Celkem A	6 + 3 + 2	11 cm²

S_A = 6 + 3 + 2 = 11 cm²

2 Spočítáme obsah obrazce B

Obrazec B taky rozložíme na části:

Kousek	Výpočet	Obsah
Obdélníková část	počítáme čtverečky	4 cm²
Trojúhelník 1	základna × výška : 2	2 cm²
Trojúhelník 2	základna × výška : 2	2 cm²
Trojúhelník 3	základna × výška : 2	2 cm²
Celkem B	4 + 2 + 2 + 2	10 cm²

S_B = 4 + 2 + 2 + 2 = 10 cm²

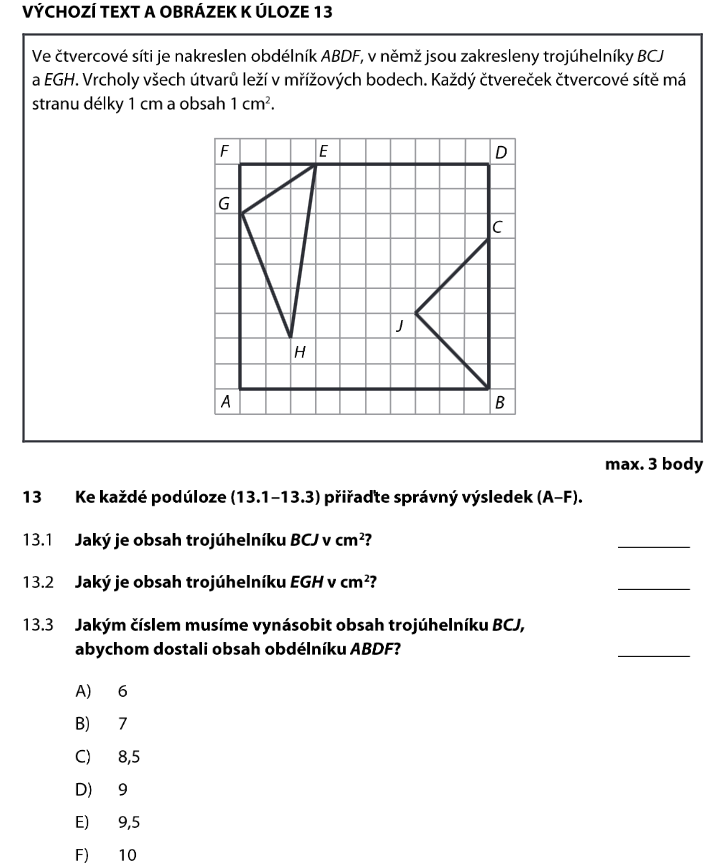
Obsahy se nerovnají: 11 ≠ 10.

3 Co s obvodem obrazce B?

Obrazec B má některé strany šikmo — jdou přes úhlopříčku čtverečku. A úhlopříčka čtverečku s délkou strany 1 cm není celé číslo!

úhlopříčka čtverečku ≈ 1,41 cm

Takže obvod obrazce B nemůže být přesně 16 cm (to je celé číslo). Obvod obsahuje úhlopříčky, takže výsledek bude desetinné číslo.

4 Odpovídáme na všechna tvrzení

Tvrzení	Pravda?	Proč?
8.1) Obsahy obou obrazců si jsou rovny.	N	A = 11 cm², B = 10 cm² → nerovnají se
8.2) Obsah obrazce A je 11 cm².	A	Spočítali jsme: přesně 11 cm²
8.3) Obvod obrazce B je 16 cm.	N	Šikmé strany → obvod není celé číslo

✅ Výsledek

8.1) N 8.2) A 8.3) N

💡 Tip pro CERMAT

Obvod obrazce ve čtvercové síti:

Strany podél mřížky = celá čísla (počet čtverečků)
Šikmé strany (úhlopříčky) = nejsou celá čísla! Proto výsledný obvod bude taky desetinné číslo.
Když vidíš šikmé strany a odpověď je celé číslo — je to chyták!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 13 (3 body)

Obdélník ABDF má rozměry 10 × 9 (v mřížových bodech). Uvnitř jsou trojúhelníky BCJ a EGH s vrcholy v mřížových bodech. Přiřaď:

13.1) Obsah trojúhelníku BCJ v cm²?

13.2) Obsah trojúhelníku EGH v cm²?

13.3) Jakým číslem násobíme obsah BCJ, abychom dostali obsah obdélníku ABDF?

Možnosti: A) 6 B) 7 C) 8,5 D) 9 E) 9,5 F) 10

1 Obsah trojúhelníku BCJ

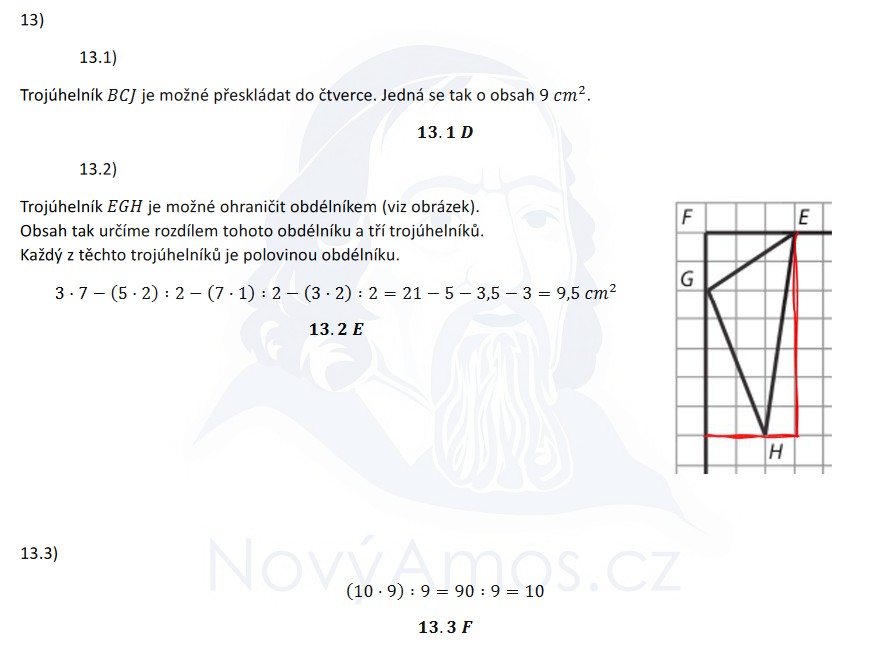
Trojúhelník BCJ má vrcholy v mřížových bodech. Podíváme se na jeho základnu a výšku:

S_BCJ = základna × výška : 2

Když si najdeme správnou základnu a výšku na mřížce, vyjde nám:

S_BCJ = 9 cm²

Trik: tento trojúhelník se dá přeskládat do čtverce 3 × 3 = 9 cm².

2 Obsah trojúhelníku EGH

EGH je šikmý trojúhelník — použijeme metodu obdélník minus trojúhelníky:

Obkreslíme EGH nejmenším obdélníkem: 3 × 7 = 21 cm²

Odečteme 3 rohové trojúhelníky:

T₁ = 5 cm² T₂ = 3,5 cm² T₃ = 3 cm²

S_EGH = 21 − 5 − 3,5 − 3 = 9,5 cm²

3 Jakým číslem násobíme obsah BCJ?

Obsah obdélníku ABDF:

S_ABDF = 10 × 9 = 90 cm²

Kolikrát se obsah BCJ vejde do obdélníku?

90 : 9 = 10

Obsah BCJ musíme vynásobit 10, abychom dostali obsah obdélníku.

✅ Výsledek

13.1) D (9 cm²) 13.2) E (9,5 cm²) 13.3) F (10)

💡 Tip pro CERMAT

U šikmých trojúhelníků vždy použij metodu obdélník minus trojúhelníky — je spolehlivá!
Přiřazovací úlohy: spočítej všechno krok po kroku, pak přiřaď správnou možnost
Pozor na desetinná čísla — obsah trojúhelníku může vyjít 9,5 cm². To je v pořádku!

📝 Oficiální řešení CERMAT

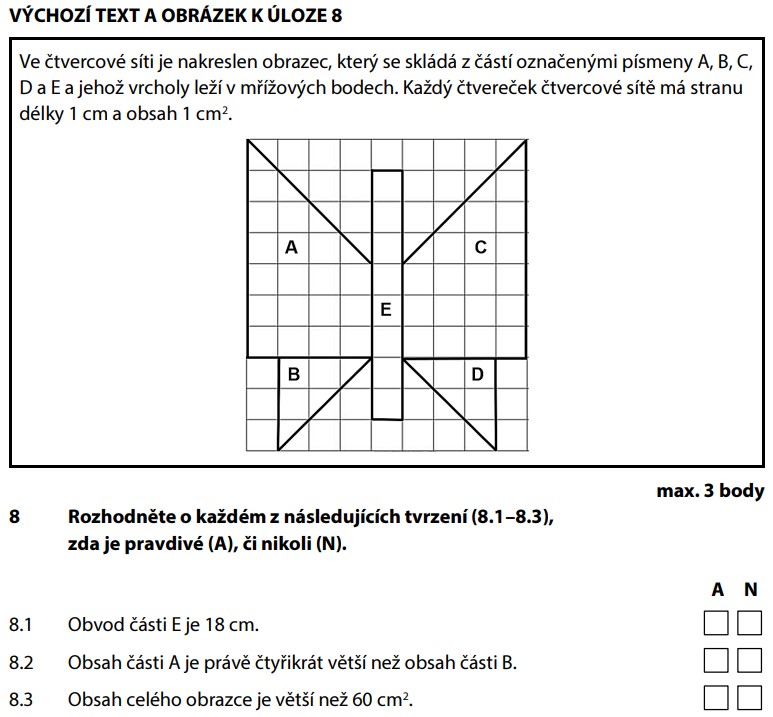
📋 Zadání — 1. náhradní termín, Úloha 8 (3 body)

Obrazec je složený z částí A, B, C, D, E ve čtvercové síti (strana čtverečku je 1 cm). Rozhodni, jestli platí (A), nebo neplatí (N):

8.1) Obvod části E je 18 cm.

8.2) Obsah části A je právě 4× větší než obsah části B.

8.3) Obsah celého obrazce je větší než 60 cm².

1 Obvod části E

Část E je obdélník s rozměry 1 × 8.

Obvod obdélníku = 2 × (délka + šířka):

O_E = 2 × (1 + 8) = 2 × 9 = 18 cm

Tvrzení 8.1 je pravdivé — obvod je přesně 18 cm.

2 Obsahy částí A a B

Část A je složitější tvar — rozložíme ho:

S_A = trojúhelník + obdélník = (4 × 4) : 2 + 3 × 4 = 8 + 12 = 20 cm²

Část B je pravoúhlý trojúhelník:

S_B = (3 × 3) : 2 = 4,5 cm²

Je obsah A právě 4× větší než B?

4 × 4,5 = 18 ale S_A = 20 → 18 ≠ 20

Tvrzení 8.2 je nepravdivé. Poměr je jiný než přesně 4×.

3 Obsah celého obrazce

Sečteme obsahy všech pěti částí:

Část	Obsah
A	20 cm²
B	4,5 cm²
C	20 cm²
D	4,5 cm²
E	8 cm²
Celkem	57 cm²

20 + 4,5 + 20 + 4,5 + 8 = 57 cm²

57 < 60, takže tvrzení 8.3 je nepravdivé.

✅ Výsledek

8.1) A 8.2) N 8.3) N

⚠️ CERMAT chyták

Slovo "právě 4× větší" znamená přesně 4×. Nestačí, aby to bylo "skoro" nebo "přibližně" 4×.

4 × 4,5 = 18, ale A má obsah 20 → není to přesně 4×
Vždy si dej pozor na slovo právě — znamená na chlup přesně!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 8 (3 body)

Obdélník ABCD má rozměry 5 × 4 čtverečky a jeho obvod je 54 cm. Uvnitř je tmavý obrazec. Rozhodni, jestli platí (A), nebo neplatí (N):

8.1) Obsah obdélníku ABCD je 180 cm².

8.2) Obvod tmavého obrazce je 69 cm.

8.3) Obsah tmavého obrazce je 90 cm².

1 Jak velký je jeden čtvereček?

Obdélník má 5 × 4 čtverečky a obvod 54 cm. Nejdřív zjistíme, jak dlouhá je strana jednoho čtverečku.

Obvod obdélníku = 2 × (délka + šířka):

O = 2 × (5a + 4a) = 2 × 9a = 18a

Kde a je strana čtverečku. Víme, že obvod = 54:

18a = 54 → a = 54 : 18 = 3 cm

Jeden čtvereček má stranu 3 cm (ne 1 cm jako jindy!).

2 Obsah obdélníku ABCD

Obdélník má 5 × 4 čtverečky, každý o straně 3 cm:

S_ABCD = (5 × 3) × (4 × 3) = 15 × 12 = 180 cm²

Tvrzení 8.1 je pravdivé.

3 Obvod tmavého obrazce

Spočítáme, kolik stran čtverečků tvoří obvod tmavého obrazce. Na obrázku obkreslíme hranici tmavého tvaru:

Počet stran čtverečků na obvodu = 24

Každá strana měří 3 cm:

O_tmavý = 24 × 3 = 72 cm

Tvrzení říká 69 cm, ale správně je 72 cm → tvrzení 8.2 je nepravdivé.

4 Obsah tmavého obrazce

Spočítáme, kolik celých čtverečků tmavý obrazec zabírá:

Počet čtverečků = 11

Každý čtvereček má obsah 3 × 3 = 9 cm²:

S_tmavý = 11 × 9 = 99 cm²

Tvrzení říká 90 cm², ale správně je 99 cm² → tvrzení 8.3 je nepravdivé.

✅ Výsledek

8.1) A 8.2) N 8.3) N

⚠️ CERMAT chyták

Pozor! V tomto příkladu strana čtverečku NENÍ 1 cm, ale 3 cm. To je velký chyták!

Vždy si nejdřív zjisti, jak velký je čtvereček — nemůžeš automaticky předpokládat, že strana = 1 cm
Obvod ti pomůže zjistit stranu čtverečku (z obvodu si ji "vybalíš")
Pak všechno počítej se správnou délkou strany

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Obsahy ve čtvercové síti

Co si odnést z tohoto tématu

🧭 Strategie řešení

Rozděl složitý tvar na obdélníky a trojúhelníky — sečti jejich obsahy
Trojúhelník = polovina obdélníku se stejnou základnou a výškou (základna × výška : 2)
U A/N tvrzení: spočítej přesně, pak porovnej s tvrzením
Obvod: sečti VŠECHNY strany — i ty malinké kousky, které jsou snadno přehlédnutelné

⚠️ Typické chytáky

Úhlopříčka čtverce NENÍ celé číslo — když obrazec má šikmé strany, obvod nebude celé číslo
Zaměnit obsah a obvod — CERMAT se ptá na obojí ve stejném příkladu, dej pozor, co počítáš!
"Právě 4× větší" — musí být PŘESNĚ 4×, ne přibližně. Slovo "právě" = na chlup přesně!
Strana čtverečku nemusí být 1 cm! — vždy si ověř z dalších údajů (např. z obvodu)

❌ Nejčastější chyby

Zapomenout na úhlopříčky při počítání obvodu — šikmé strany jsou delší než rovné
Špatně rozdělit tvar na části — přehlédnout kousek nebo ho spočítat dvakrát
U obdélníku zapomenout zjistit skutečnou stranu čtverečku — ne vždy je to 1 cm!
U trojúhelníku zapomenout vydělit dvěma — obsah trojúhelníku ≠ obsah obdélníku

📐 Obsahy ve čtvercové síti

🔑 Jak počítat obsahy ve čtvercové síti

🎯 Rady pro CERMAT: Obsahy ve čtvercové síti