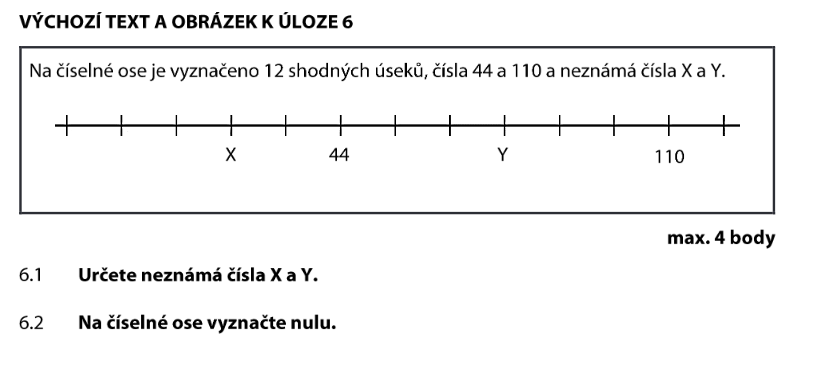
Na číselné ose najdeme dva body, jejichž hodnoty známe: 44 a 110.
Spočítáme, kolik úseků je mezi nimi. Z obrázku vidíme, že mezi 44 a 110 je 6 úseků.
Rozdíl hodnot vydělíme počtem úseků:
Jeden úsek na číselné ose odpovídá číslu 11.
X je 2 úseky před (vlevo od) čísla 44:
Y je 3 úseky před (vlevo od) čísla 110:
Nula musí být nalevo od 44. Kolik úseků potřebujeme?
Nula je o 4 úseky vlevo od 44, což je o 2 úseky vlevo od X.
U číselných os vždy začni tím, že najdeš dva body se známými hodnotami. Spočítej kolik úseků je mezi nimi, vyděl rozdíl a máš délku jednoho úseku. Pak už jen násobíš!

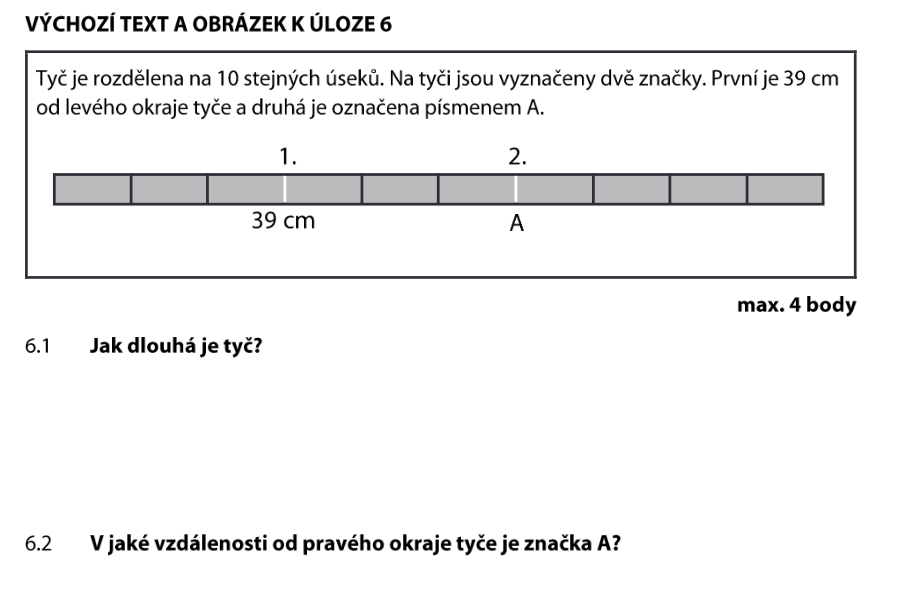
Značka „1." je po 3 dílcích od levého okraje a je 39 cm daleko:
Jeden dílek měří 13 cm.
Tyč má 10 dílků:
Značka A je na rozhraní 6. a 7. dílu — tedy po 6 dílcích od levého okraje. Od A do pravého okraje zbývá:
Pozor na rozdíl „od levého okraje" vs. „od pravého okraje"! Cermat se ptá na vzdálenost od pravého okraje, ale zadává údaj od levého. Nezapomeň přepočítat!

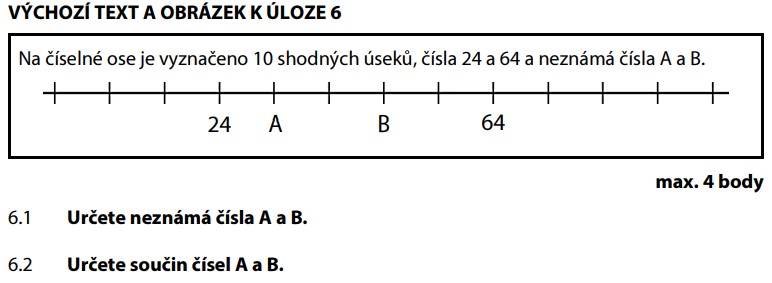
24 je na 2. značce, 64 je na 7. značce. Počet úseků mezi nimi:
Jeden úsek odpovídá číslu 8.
A je na 3. značce — o 1 úsek napravo od 24:
B je na 5. značce — o 3 úseky napravo od 24:
Teď stačí vynásobit:
Rozložíme si to na jednodušší násobení:
Když máš násobit dvě velká čísla (32 × 48), zkus si jedno zaokrouhlit a pak opravit: 32 × 50 = 1600, a odečti 32 × 2 = 64. Výsledek: 1536. Tenhle trik ti ušetří spoustu času!

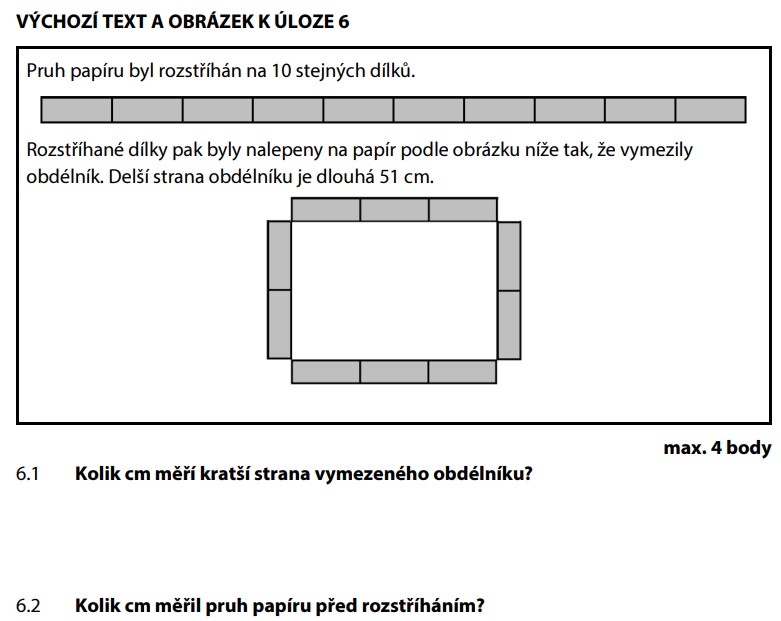
Delší strana obdélníku je složena ze 3 dílků a měří 51 cm:
Jeden dílek měří 17 cm.
Kratší strana je složena ze 2 dílků:
Celkem bylo 10 dílků (3 + 3 + 2 + 2 = 10 ✅). Celý pruh měřil:
Pozor: 3 dílky na delší straně neznamená, že obvod je 3 dílky! Obvod obdélníku tvoří všechny 4 strany (3 + 3 + 2 + 2 = 10 dílků). Vždy si ověř, že počet dílků na všech stranách dává dohromady celkový počet dílků.

🎯 Rady pro CERMAT: Obvody a délky
Co si odnést z tohoto tématu
- Najdi dva body se známými hodnotami — na číselné ose, na tyči, kdekoliv
- Spočítej kolik úseků je mezi nimi — pozor, počítej MEZERY, ne značky!
- Vyděl rozdíl počtem úseků — dostaneš délku jednoho úseku
- Pak násobením dopočítej všechno ostatní (neznámé hodnoty, nulu, celkovou délku)
- Špatný počet úseků — počítej MEZERY (úseky) mezi značkami, ne samotné značky! Mezi značkou 2 a 7 je 5 úseků, ne 7
- U pruhu papíru: 3 dílky na straně = délka strany, ne obvod — obvod je součet všech 4 stran
- Nezapomeň na rozdíl „od levého" vs. „od pravého" okraje — CERMAT to rád zamotá
- Zaměnit počet značek a počet úseků — mezi N značkami je N−1 úseků!
- U obdélníku z dílků spočítat špatně, kolik dílků je na které straně
- Zapomenout zkontrolovat, že součet dílků na všech stranách odpovídá celkovému počtu