Technika dílků | CERMAT 2024

📋 Zadání — 1. řádný termín, Úloha 11 (2 body)

Šestiúhelník ABCDEF lze úsečkami AD, BE a CF rozdělit na 6 shodných rovnoramenných trojúhelníků. Body A, B, D a E leží ve vrcholech obdélníku. Obsah tmavé části šestiúhelníku je 112 cm². Jaký je obsah bílé části šestiúhelníku?

Možnosti:

A) 28 cm² B) 112 cm² C) 196 cm² D) 224 cm² E) jiný obsah

1 Rozřežeme šestiúhelník na menší dílky

Šestiúhelník je rozdělen na 6 shodných trojúhelníků. Ale my půjdeme ještě dál — každý trojúhelník rozřízneme přes střed na 2 pravoúhlé trojúhelníčky.

Celkem dostaneme 12 shodných dílků (jako 12 dílků pizzy!).

2 Kolik dílků je tmavých?

Podíváme se na obrázek — tmavá část zabírá 4 dílky z 12.

Tmavá = 4 dílky → to je 1/3 celku

3 Kolik dílků je bílých?

Bílá část je zbytek:

Bílá = 12 − 4 = 8 dílků → to je 2/3 celku

Bílých dílků je dvakrát víc než tmavých!

4 Dopočítáme obsah

Tmavá = 4 dílky = 112 cm². Bílá = 8 dílků, to je 2× tolik:

Bílá = 2 × 112 = 224 cm²

✅ Výsledek

D) 224 cm²

💡 Tip pro CERMAT

Když máš složitý útvar, zkus ho rozdělit na co nejmenší shodné dílky. Pak stačí spočítat, kolik dílků je v jedné části a kolik v druhé.

📝 Oficiální řešení CERMAT

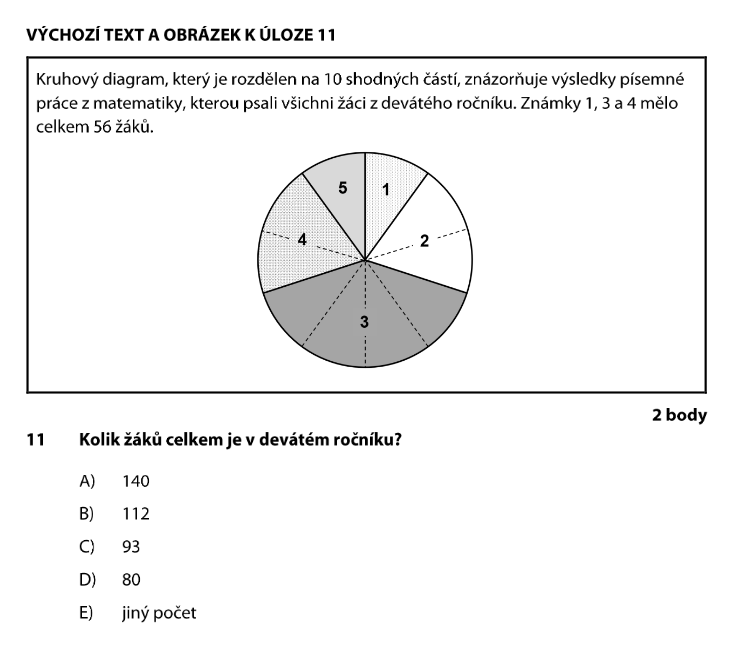
📋 Zadání — 2. řádný termín, Úloha 11 (2 body)

Kruhový diagram rozdělený na 10 shodných částí znázorňuje výsledky písemné práce z matematiky. Známky 1, 3 a 4 mělo celkem 56 žáků. Kolik žáků celkem je v devátém ročníku?

Diagram:

Známka 1: 1 výseč | Známka 2: 2 výseče | Známka 3: 3 výseče | Známka 4: 3 výseče | Známka 5: 1 výseč

Možnosti:

A) 140 B) 112 C) 93 D) 80 E) jiný počet

1 Kolik výsečí mají známky 1, 3 a 4?

Z diagramu sečteme výseče pro známky, o kterých víme počet žáků:

Známka 1: 1 + Známka 3: 3 + Známka 4: 3 = 7 výsečí

2 Zjistíme hodnotu jednoho dílku

7 výsečí = 56 žáků. Kolik žáků připadá na jednu výseč?

56 : 7 = 8 žáků na výseč

Každý dílek koláčového grafu = 8 žáků.

3 Spočítáme celkový počet žáků

Celý diagram má 10 výsečí:

10 × 8 = 80 žáků

✅ Výsledek

D) 80 žáků

💡 Tip pro CERMAT

U kruhových diagramů vždy:

Sečti výseče pro skupiny, kde znáš celkový počet
Vyděl, abys zjistil hodnotu jedné výseče
Vynásob celkovým počtem výsečí

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 9 (2 body)

Kilogram broskví stojí 32 Kč a kilogram jablek 28 Kč. Petra koupila stejný počet kilogramů jablek jako broskví a utratila 720 Kč. Kolik kilogramů broskví Petra koupila?

Možnosti:

A) 6 B) 8 C) 10 D) 12 E) jiný počet

1 Vytvoříme si „pár"

Petra koupila stejný počet kg jablek a broskví. Představ si, že kupuje vždy pár: 1 kg broskví + 1 kg jablek najednou.

2 Kolik stojí jeden pár?

Jeden pár = 1 kg broskví + 1 kg jablek:

32 + 28 = 60 Kč za pár

3 Kolik párů koupila?

Celkem utratila 720 Kč. Kolik párů po 60 Kč si může koupit?

720 : 60 = 12 párů

4 Odpovíme na otázku

12 párů = 12 kg broskví (a taky 12 kg jablek).

Broskví = 12 kg

✅ Výsledek

D) 12 kg

💡 Tip pro CERMAT

Když kupuješ stejný počet dvou věcí, sečti jejich ceny — dostaneš cenu jednoho „páru". Pak jen vyděl celkovou částku cenou páru.

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 11 (2 body)

Do čtvercové sítě 3×3 (9 čtverečků) je zakreslen šedý čtyřúhelník s vrcholy v mřížových bodech. Alena říká: více než polovina. Blanka říká: polovina. Cecílie říká: tři šestiny. Darina říká: tři pětiny. Kdo odpověděl správně?

Možnosti:

A) Alena a Darina B) Blanka a Cecílie C) jenom Alena D) jenom Darina E) ani jedna

1 Spočítáme bílé části

Místo počítání šedé části je jednodušší spočítat bílé kousky a odečíst je od celku. Bílé rohy a trojúhelníčky mají dohromady:

1,5 + 2 + 1 = 4,5 čtverečků

2 Kolik je šedá část?

Celá síť má 9 čtverečků. Šedá část:

9 − 4,5 = 4,5 čtverečků

Šedá = 4,5 z 9 = polovina celku!

3 Kdo má pravdu?

Podíváme se na odpovědi:

Alena (více než polovina) — NE, je to přesně polovina
Blanka (polovina) — ANO! ✅
Cecílie (tři šestiny = 3/6) — 3/6 = 1/2 = polovina — ANO! ✅
Darina (tři pětiny = 3/5) — NE, 3/5 je víc než 1/2

✅ Výsledek

B) Blanka a Cecílie

⚠️ CERMAT chyták

Zlomek 3/6 = 1/2 — zlomky se dají krátit! CERMAT schválně nabízí zlomek, který vypadá jinak, ale po zkrácení je to totéž. Vždy si zlomky zkrať do základního tvaru!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 9 (2 body)

Jedno balení stavebnice obsahuje 180 kostek. Jedna desetina je modrá a jedna devítina červená. Kolik balení musíme koupit, abychom měli dohromady 190 modrých a červených kostek?

Možnosti:

A) 1 B) 3 C) 5 D) 10 E) jiný výsledek

1 Kolik modrých je v jednom balení?

Jedna desetina ze 180 kostek je modrá:

180 : 10 = 18 modrých kostek

2 Kolik červených je v jednom balení?

Jedna devítina ze 180 kostek je červená:

180 : 9 = 20 červených kostek

3 Kolik barevných kostek je v jednom balení?

Sečteme modré a červené:

18 + 20 = 38 barevných kostek v jednom balení

4 Kolik balení potřebujeme?

Chceme 190 barevných kostek celkem. Kolik balení po 38 kusech to bude?

190 : 38 = 5 balení

✅ Výsledek

C) 5 balení

⚠️ CERMAT chyták

Pozor na rozdíl: jedna desetina (dělíme 10) a jedna devítina (dělíme 9) — vypadají podobně, ale výsledky jsou jiné! Vždy si pečlivě přečti, čím dělíš.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 11 (2 body)

Kruhový diagram (10 dílů) znázorňuje prodej ovoce a zeleniny. Jablka: 5 dílů, hrušky: 3 díly, cibule: 1 díl, mrkve: 1 díl. Cibule a hrušek se prodalo dohromady 76 kg. Kolik kg ovoce (jablek a hrušek) se celkem prodalo?

Možnosti:

A) 152 B) 95 C) 57 D) 38 E) jiný počet

1 Kolik dílů mají cibule a hrušky?

Z diagramu sečteme dílky pro to, co známe:

Cibule: 1 díl + Hrušky: 3 díly = 4 díly

2 Zjistíme hodnotu jednoho dílku

Cibule + hrušky = 4 díly = 76 kg. Kolik kg je jeden dílek?

76 : 4 = 19 kg na díl

3 Kolik dílů je ovoce?

Ovoce = jablka + hrušky:

Jablka: 5 dílů + Hrušky: 3 díly = 8 dílů

4 Spočítáme kg ovoce

8 dílů × 19 kg:

8 × 19 = 152 kg

✅ Výsledek

A) 152 kg

💡 Tip pro CERMAT

Pozor na otázku! Ptají se na ovoce (jablka + hrušky), ne na všechno. Vždy si přečti, co přesně se ptají — můžeš mít správný postup, ale špatnou odpověď, protože jsi sečetl jiné skupiny.

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Technika dílků

Co si odnést z tohoto tématu

🧭 Strategie řešení

Najdi celek a rozděl ho na stejné dílky (výseče, trojúhelníky, páry...)
Zjisti hodnotu jednoho dílku — vyděl známou hodnotu počtem dílků
Pak násobením dopočítej to, na co se ptají
U kruhových diagramů: sečti výseče pro skupiny, kde znáš celkový počet

⚠️ Typické chytáky

Špatný počet dílků — pečlivě počítej výseče nebo části na obrázku
U kruhových diagramů nepřesné přiřazení výsečí ke kategoriím
Zlomky se dají krátit — 3/6 = 1/2, CERMAT to dává schválně!
Pozor: „jedna desetina" vs „jedna devítina" — vypadají podobně, ale jsou to jiná čísla

❌ Nejčastější chyby

Zapomenout na jednu skupinu při počítání dílků
Zaměnit celek za část — pozor, co přesně se ptají (celkový počet vs. jen jedna skupina)
Nepřečíst si otázku pořádně — ptají se na ovoce, nebo na všechno?

🧩 Technika dílků

🔑 Jak funguje technika dílků

🎯 Rady pro CERMAT: Technika dílků