Pořadí operací a závorky

📋 Zadání — 1. řádný termín, Úloha 1 (4 body)

Vypočítejte:

1.1)

5 · 115 + (232 + 21 · 8) : (5 + 60 : 3) =

1.2)

(128 + 16 : 4 − 32) : (30 + 5 · 13 − 9 · 5) − 1 =

1 Příklad 1.1 — najdeme operace uvnitř závorek

Máme dvě závorky. V každé najdeme násobení nebo dělení — to počítáme první:

5 · 115 + (232 + 21 · 8) : (5 + 60 : 3)

Spočítáme: 21 · 8 = 168 a 60 : 3 = 20

2 Příklad 1.1 — dokončíme závorky

Dosadíme výsledky a dopočítáme obě závorky:

5 · 115 + (232 + 168) : (5 + 20)

5 · 115 + 400 : 25

První závorka = 400, druhá závorka = 25. Výborně!

3 Příklad 1.1 — násobení a dělení mají přednost

Závorky jsou pryč. Teď hledáme · a : (ty se počítají dřív než +):

5 · 115 + 400 : 25

575 + 16

A nakonec sečteme: 575 + 16 = 591

4 Příklad 1.2 — operace uvnitř závorek

Zase máme dvě závorky. V každé najdeme · a : :

(128 + 16 : 4 − 32) : (30 + 5 · 13 − 9 · 5) − 1

Spočítáme: 16 : 4 = 4, pak 5 · 13 = 65, a 9 · 5 = 45

5 Příklad 1.2 — dokončíme závorky

Dosadíme a dopočítáme závorky (sčítání a odčítání zleva doprava):

(128 + 4 − 32) : (30 + 65 − 45) − 1

100 : 50 − 1

První závorka: 128 + 4 = 132, pak 132 − 32 = 100

Druhá závorka: 30 + 65 = 95, pak 95 − 45 = 50

6 Příklad 1.2 — dopočítáme výsledek

Závorky máme hotové. Pozor — dělení se počítá dřív než odčítání!

100 : 50 − 1

2 − 1 = 1

Nejdřív 100 : 50 = 2, a pak teprve 2 − 1 = 1. Skvělé! 🎉

✅ Výsledek

1.1) = 591 1.2) = 1

💡 Tip pro CERMAT

Klasická „Cermatovina" — dva příklady s několika závorkami. Postup je vždycky stejný:

Najdi závorky — ty řeš první
Uvnitř závorek hledej · a : (mají přednost před + a −)
Po vyřešení závorek se vrať k pravidlům: · a : dřív, pak + a −

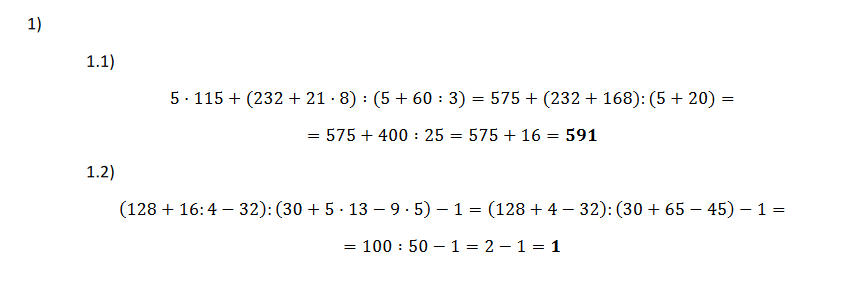
📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 1 (4 body)

Vypočítejte:

1.1)

25 + 3 · (75 − 2 · 25) − (25 − 5) · 2 − 25 =

1.2)

6 · 7 + (50 + 50 : 5) : (28 : 7) + 3 · 8 =

1 Příklad 1.1 — násobení uvnitř závorky

V první závorce najdeme násobení — to počítáme první:

25 + 3 · (75 − 2 · 25) − (25 − 5) · 2 − 25

2 · 25 = 50

2 Příklad 1.1 — dokončíme závorky

Dopočítáme obě závorky:

25 + 3 · (75 − 50) − (25 − 5) · 2 − 25

25 + 3 · 25 − 20 · 2 − 25

První závorka: 75 − 50 = 25. Druhá závorka: 25 − 5 = 20.

3 Příklad 1.1 — násobení má přednost

Závorky jsou pryč. Teď spočítáme násobení:

25 + 3 · 25 − 20 · 2 − 25

25 + 75 − 40 − 25

A nakonec sčítání a odčítání zleva doprava:

25 + 75 = 100, 100 − 40 = 60, 60 − 25 = 35

4 Příklad 1.2 — operace uvnitř závorek

Najdeme závorky a uvnitř nich hledáme · a : :

6 · 7 + (50 + 50 : 5) : (28 : 7) + 3 · 8

Spočítáme: 50 : 5 = 10 a 28 : 7 = 4

5 Příklad 1.2 — dokončíme závorky a dopočítáme

Dokončíme závorky:

6 · 7 + (50 + 10) : 4 + 3 · 8

42 + 60 : 4 + 24

Teď násobení a dělení: 6 · 7 = 42, 60 : 4 = 15, 3 · 8 = 24

42 + 15 + 24 = 81

✅ Výsledek

1.1) = 35 1.2) = 81

💡 Tip pro CERMAT

Všimni si, jak CERMAT rád opakuje číslo 25 v příkladu 1.1. Chce tě zmást, abys to sčítal nebo zaměnil. Dávej si pozor a vždycky přesně sleduj, kde které číslo patří!

Každou závorku si podtrhni a vyřeš zvlášť
Násobení u závorky (např. 3 · závorka) počítej až po vyřešení závorky

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 1 (4 body)

Vypočítejte:

1.1)

(12 · 12) : 6 + 12 · 6 =

1.2)

(1970 + 8 · 23) − (1971 − 21 : 7) =

1 Příklad 1.1 — závorka a násobení

Začneme závorkou — ta je první na řadě:

(12 · 12) : 6 + 12 · 6

12 · 12 = 144

2 Příklad 1.1 — dělení a násobení mají přednost

Závorka je hotová. Teď najdeme dělení a násobení:

144 : 6 + 12 · 6

24 + 72

A nakonec sečteme: 24 + 72 = 96

3 Příklad 1.2 — operace uvnitř závorek

Máme dvě závorky. V každé hledáme · a : :

(1970 + 8 · 23) − (1971 − 21 : 7)

8 · 23 = 184 a 21 : 7 = 3

4 Příklad 1.2 — dokončíme závorky

Dosadíme a dopočítáme:

(1970 + 184) − (1971 − 3)

2154 − 1968

První závorka: 1970 + 184 = 2154

Druhá závorka: 1971 − 3 = 1968

5 Příklad 1.2 — výsledek

Odečteme:

2154 − 1968 = 186

Tady pomůže trik: 2154 − 1968 = 2154 − 2000 + 32 = 154 + 32 = 186. Super! 🎉

✅ Výsledek

1.1) = 96 1.2) = 186

💡 Tip pro CERMAT

Příklad 1.1 vypadá jednoduše, ale pozor na číslo 12, které se opakuje! CERMAT rád volí stejná čísla, abys zaměnil výsledky. Pečlivě sleduj, kde je dělení a kde násobení.

Při odčítání velkých čísel (jako 2154 − 1968) si to rozlož na jednodušší kroky
Zkontroluj si: je výsledek kladný? (CERMAT většinou dává kladné výsledky)

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 1 (4 body)

Vypočítejte:

1.1)

336 + 336 : 6 − 45 =

1.2)

(725 − 25 · 8 + 500) : (75 : 3) =

1 Příklad 1.1 — pozor na chyták!

Tady nejsou závorky. Hledáme rovnou · a : — dělení má přednost před sčítáním!

336 + 336 : 6 − 45

336 : 6 = 56

⚠️ Pozor: nepočítej 336 + 336 = 672! Dělení se počítá PRVNÍ!

2 Příklad 1.1 — sčítání a odčítání

Teď už jen sčítáme a odčítáme zleva doprava:

336 + 56 − 45

336 + 56 = 392

392 − 45 = 347

Vidíš, jak to jde? Stačí dodržet správné pořadí! 🎉

3 Příklad 1.2 — operace uvnitř závorek

Máme dvě závorky. V první hledáme · a : :

(725 − 25 · 8 + 500) : (75 : 3)

25 · 8 = 200 a 75 : 3 = 25

4 Příklad 1.2 — dokončíme závorky

Dopočítáme první závorku (zleva doprava):

(725 − 200 + 500) : 25

725 − 200 = 525, 525 + 500 = 1025

První závorka = 1025, druhá závorka = 25

5 Příklad 1.2 — výsledek

Vydělíme:

1025 : 25 = 41

Jak na to? 25 · 40 = 1000, a 25 · 1 = 25. Takže 25 · 41 = 1025. Správně!

✅ Výsledek

1.1) = 347 1.2) = 41

⚠️ CERMAT chyták

Příklad 1.1 je klasická past! CERMAT napíše 336 + 336 : 6, a spousta dětí spočítá 336 + 336 = 672, protože čísla vypadají stejně. Ale dělení se počítá vždycky dřív než sčítání!

Pamatuj: 336 + 336 : 6 ≠ (336 + 336) : 6 — to jsou dva úplně jiné příklady.

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Pořadí operací

Co si odnést z tohoto tématu

🧭 Strategie řešení

Najdi a podtrhni si závorky — ty řeš vždycky první
Uvnitř závorek hledej · a : (ty mají přednost před + a −)
Po vyřešení závorek se vrať k pravidlům (· a : první, pak + a −)
Vždycky počítej zleva doprava u operací stejné priority

⚠️ Typické chytáky

Po vyřešení závorky pozor: výsledek dělení/násobení se počítá dřív než +/−
Pozor na 336 + 336 : 6 — dělení 336 : 6 se počítá PRVNÍ (ne sčítání!)
CERMAT rád dává čísla, která se opakují (336, 25, 12), aby tě zmátl

❌ Nejčastější chyby

Zapomenout na pořadí operací po vyřešení závorky
Počítat zleva doprava bez ohledu na · a :
Špatné znaménko při odčítání závorek (pozor na minus před závorkou!)

🔢 Pořadí operací a závorky

🔑 Zlaté pravidlo pořadí operací

🎯 Rady pro CERMAT: Pořadí operací