Geometrické konstrukce

📋 Zadání — 1. řádný termín, Úloha 7 (6 bodů)

7.1)

V rovině je dán bod C a přímky a, b. Bod C je vrchol trojúhelníku ABC, přičemž bod A leží na přímce a a bod B leží na přímce b. Trojúhelník ABC je rovnoramenný, platí AC = AB a úsečka AC je rovnoběžná s přímkou b. Sestrojte body A, B. Najděte všechna řešení.

7.2)

V rovině jsou dány body K, S a přímka p, která prochází bodem S. Bod K je vrchol obdélníku KLMN. Bod S je střed strany KL. Přímka p prochází středem strany KL a středem ještě jedné strany obdélníku KLMN. Sestrojte body L, M, N. Najděte všechna řešení.

1 Příklad 7.1: Co víme?

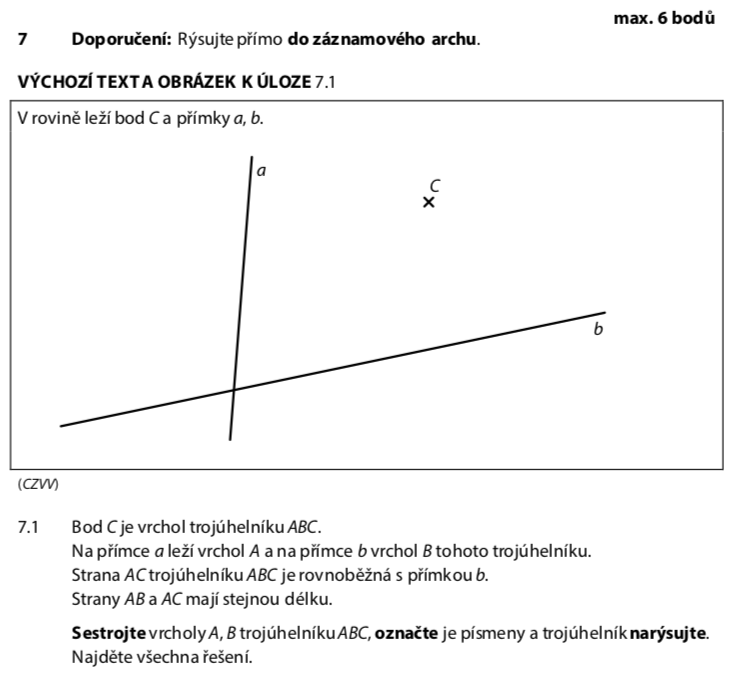
Přečteme si pozorně všechny podmínky a podtrhneme klíčová slova:

Bod C je daný
Bod A leží na přímce a
Bod B leží na přímce b
AC rovnoběžná s přímkou b → vedeme rovnoběžku!
AC = AB → rovnoramenný trojúhelník → použijeme kružnici

2 Příklad 7.1: Najdeme bod A

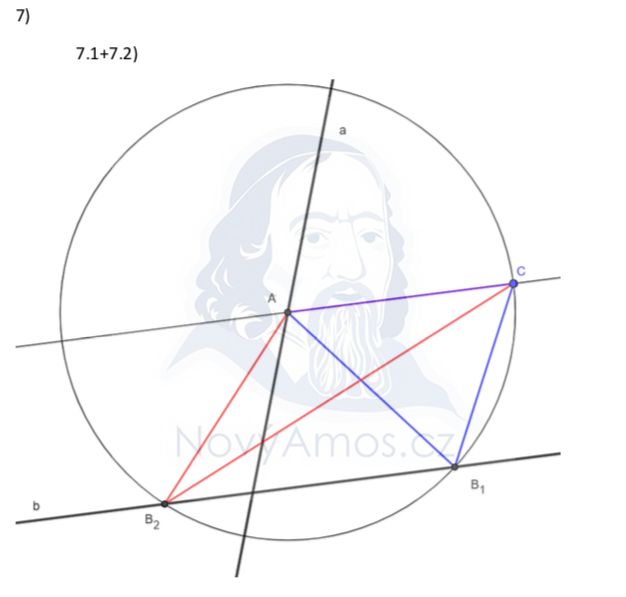
Nejdřív najdeme bod A. Víme, že AC je rovnoběžná s b.

Vedeme rovnoběžku s přímkou b procházející bodem C

Tato rovnoběžka protne přímku a v bodě A.

Bod A je jednoznačně určený! ✅

3 Příklad 7.1: Najdeme bod B pomocí kružnice

Trojúhelník je rovnoramenný, tzn. AC = AB. To znamená, že bod B musí mít od bodu A stejnou vzdálenost jako bod C!

Sestrojíme kružnice se středem A a poloměrem |AC|

Tato kružnice protne přímku b ve dvou bodech: B₁ a B₂.

Máme DVĚ řešení: trojúhelníky AB₁C a AB₂C

4 Příklad 7.2: Co víme?

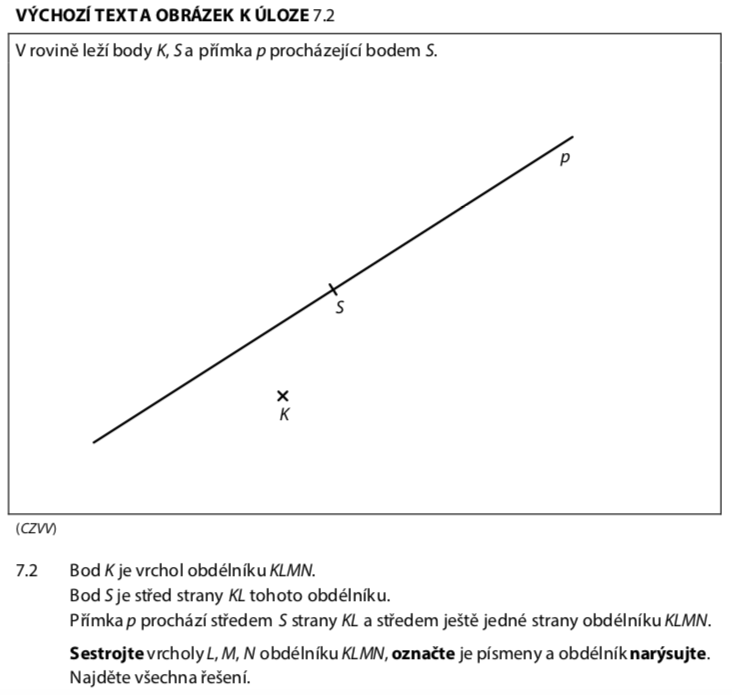
Přečteme si pozorně zadání:

Body K a S jsou dány
Přímka p prochází bodem S
S je střed strany KL → L je souměrný s K podle S!
Přímka p prochází středem KL a středem ještě jedné strany → protilehlé strany!

5 Příklad 7.2: Najdeme bod L

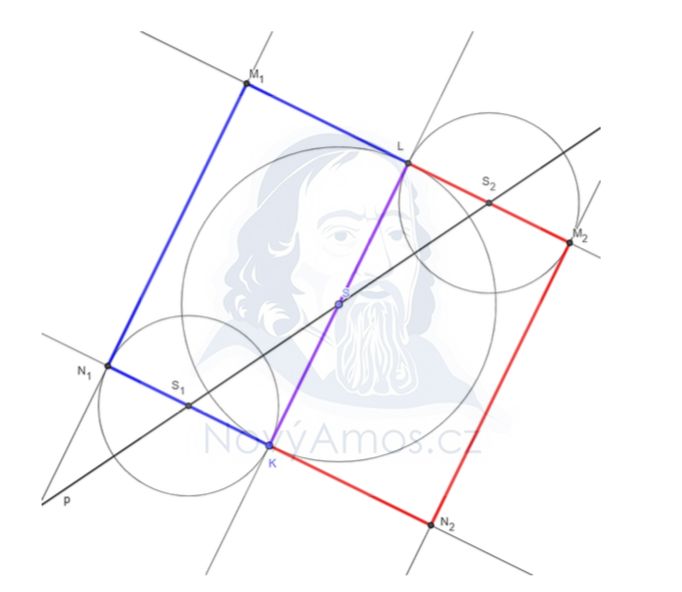
S je střed strany KL, což znamená, že |KS| = |SL|.

Bod L je souměrný s K podle S

Narýsujeme bod L tak, aby S ležel přesně uprostřed mezi K a L.

Nyní známe stranu KL. ✅

6 Příklad 7.2: Najdeme strany rovnoběžné s p

Přímka p prochází středem strany KL a středem další strany. V obdélníku to mohou být jen protilehlé strany KN a LM.

Strany KN a LM jsou rovnoběžné s přímkou p

Vedeme kolmice z bodů K a L na přímku p → dostaneme směr stran KN a LM.

Druhá dvojice stran je kolmá na přímku p → sestrojíme body M a N.

Pozor: obdélník můžeme sestrojit na obou stranách přímky KL → DVĚ řešení!

✅ Výsledek

7.1) Dva trojúhelníky AB₁C a AB₂C

7.2) Dva obdélníky KLMN

💡 Tip pro CERMAT

U rovnoramenného trojúhelníku: kružnice ti najde bod ve správné vzdálenosti → obvykle dvě řešení
Střed strany → souměrný bod je na opačné straně (S je uprostřed mezi K a L)
V obdélníku: přímka spojující středy protilehlých stran je rovnoběžná s ostatními dvěma stranami

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 7 (6 bodů)

7.1)

V rovině je dán bod F a přímka g. Bod F je vrchol rovnoramenného trojúhelníku EFG. Úsečka EF má délku 5 cm a leží na kolmici k přímce g. Bod G leží na přímce g. Sestrojte body E, G.

7.2)

V rovině jsou dány body S, Q a přímka p. Na přímce p leží dvě sousední strany obdélníku ABCD. Bod S je střed strany AD a bodem Q prochází úhlopříčka obdélníku ABCD. Sestrojte obdélník ABCD.

1 Příklad 7.1: Co víme?

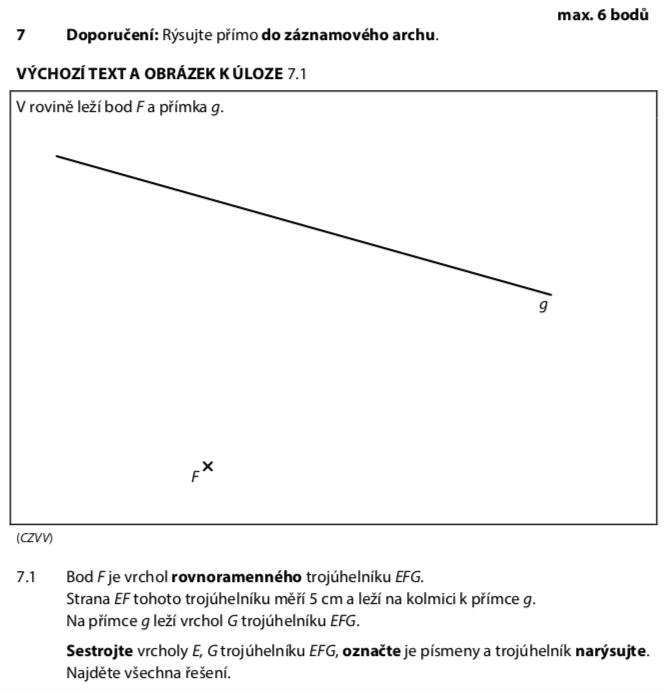
Přečteme si podmínky a podtrhneme klíčová slova:

Bod F je daný
Úsečka EF leží na kolmici k přímce g → nejdřív sestrojíme kolmici!
|EF| = 5 cm → známe vzdálenost E od F
Trojúhelník je rovnoramenný EFG → EF = FG nebo EF = EG
Bod G leží na přímce g

2 Příklad 7.1: Najdeme bod E

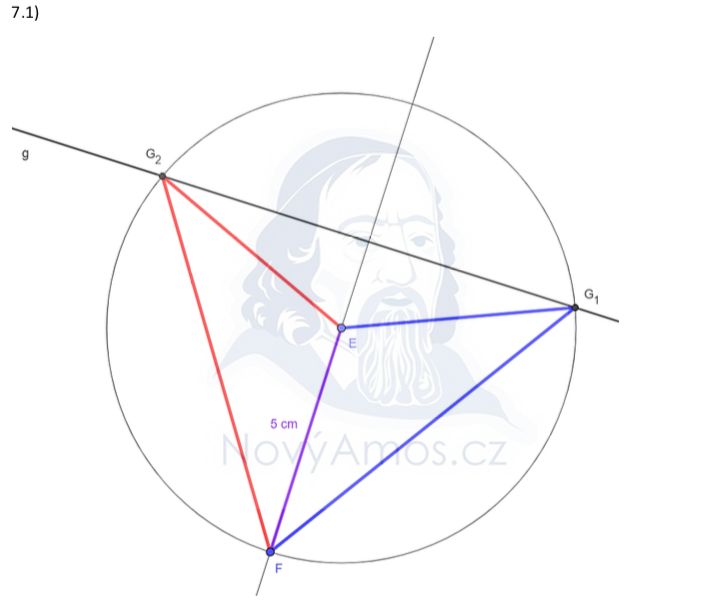
Úsečka EF leží na kolmici k přímce g.

Vedeme kolmici k přímce g procházející bodem F

Na této kolmici vyznačíme bod E ve vzdálenosti 5 cm od F.

Bod E je jednoznačně určený (nad nebo pod bodem F). ✅

3 Příklad 7.1: Najdeme bod G pomocí kružnice

Trojúhelník EFG je rovnoramenný. Která dvě ramena jsou stejně dlouhá? V našem případě EF = FG (základna je EG), nebo EF = EG (základna je FG).

Víme, že |EF| = 5 cm, takže hledáme bod G, který má od E (nebo od F) vzdálenost také 5 cm!

Sestrojíme kružnici se středem E a poloměrem 5 cm

Tato kružnice protne přímku g ve dvou bodech: G₁ a G₂.

Máme DVĚ řešení: trojúhelníky EFG₁ a EFG₂

4 Příklad 7.2: Co víme?

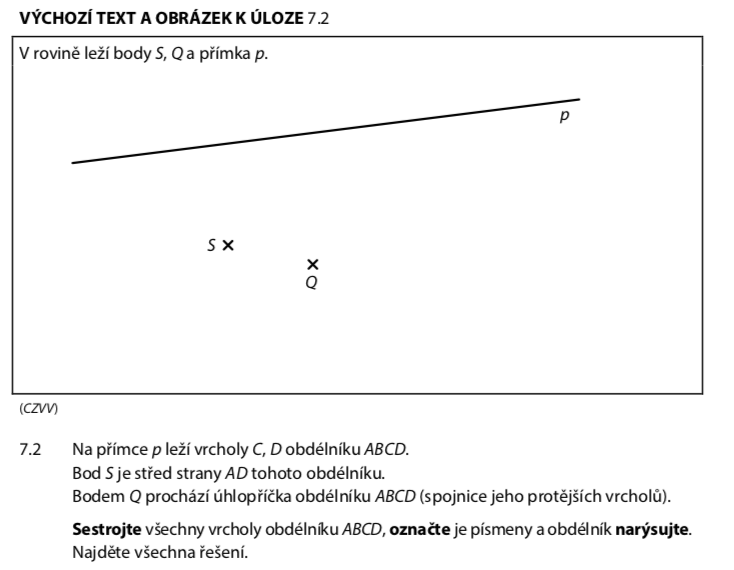
Přečteme si pozorně zadání:

Body S a Q jsou dány
Přímka p je daná
Na přímce p leží dvě sousední strany obdélníku → např. AB a BC (nebo CD a DA)
S je střed strany AD
Bodem Q prochází úhlopříčka obdélníku

5 Příklad 7.2: Najdeme bod D

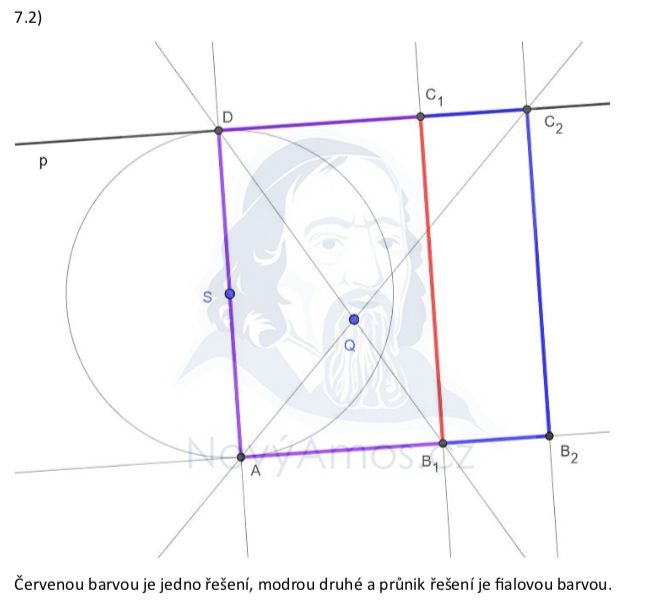
S je střed strany AD, což znamená, že AD je kolmá na p (dvě sousední strany jsou na p).

Vedeme kolmici z S na přímku p → dostaneme bod D na přímce p

Bod A je souměrný s D podle S (|SA| = |SD|).

Nyní známe stranu AD. ✅

6 Příklad 7.2: Najdeme zbylé vrcholy

Víme, že úhlopříčka prochází bodem Q. Úhlopříčka obdélníku spojuje protilehlé vrcholy (např. AC nebo BD).

Z bodu A (nebo D) vedeme přímku přes Q → dostaneme směr úhlopříčky

Tato úhlopříčka určí polohu protilehlého vrcholu (C nebo B). Sestrojíme zbylé dva vrcholy tak, aby vznikl obdélník.

Pozor: obdélník můžeme sestrojit dvěma způsoby (záleží, která úhlopříčka prochází Q) → DVĚ řešení!

✅ Výsledek

7.1) Dva trojúhelníky EFG

7.2) Dva obdélníky ABCD

💡 Tip pro CERMAT

Kolmice k přímce → použij kružítko nebo trojúhelník s pravým úhlem
U rovnoramenného trojúhelníku: kružnice ti pomůže najít bod ve správné vzdálenosti
Střed strany → souměrný bod podle středu

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 7 (5 bodů)

7.1)

V rovině je dána úsečka KL a přímka a. Body K, L leží uvnitř dvou různých stran obdélníku ABCD. Strana AB leží na přímce a. Některá ze stran obdélníku ABCD má délku dvakrát větší než je délka úsečky KL. Sestrojte obdélník ABCD.

7.2)

V rovině jsou dány přímky p, q, kde přímka q prochází bodem R. Bod R je vrchol pravoúhlého rovnoramenného trojúhelníku PQR se základnou PQ. Bod P leží na přímce p a bod Q leží na přímce q. Sestrojte trojúhelník PQR.

1 Příklad 7.1: Co víme?

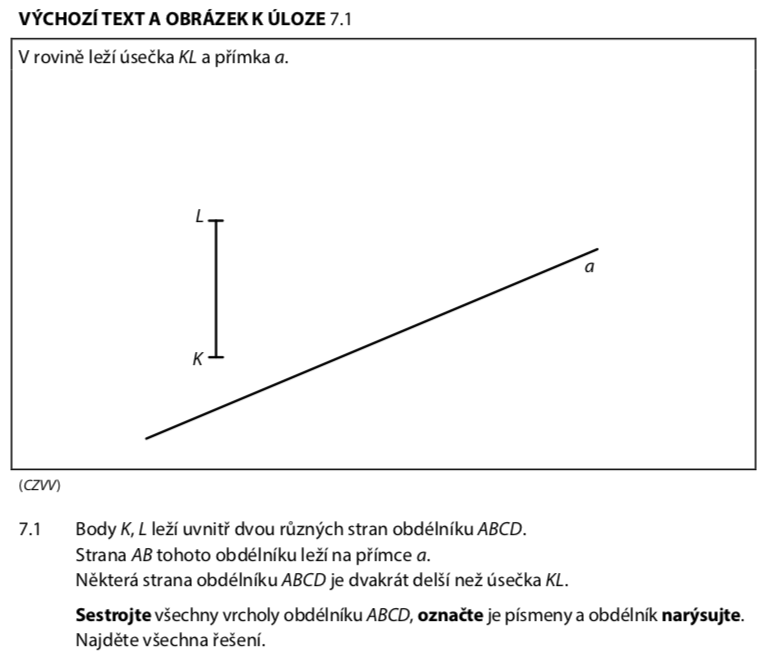
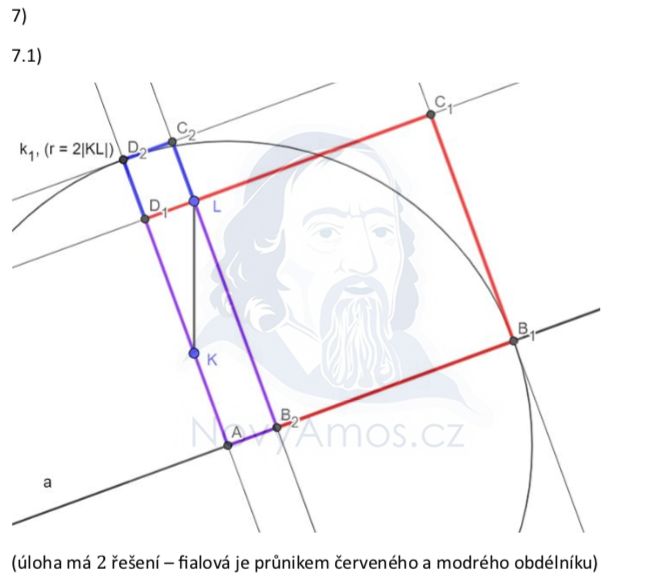
Přečteme si pozorně podmínky:

Úsečka KL je daná
Přímka a je daná
Body K, L leží uvnitř dvou různých stran obdélníku
Strana AB leží na přímce a
Některá strana má délku 2 × |KL| → klíčová informace!

2 Příklad 7.1: Sestrojíme obdélník

Víme, že jedna strana obdélníku má délku 2 × |KL|. To nám dává velikost obdélníku!

Sestrojíme kružnici se středem K (nebo L) a poloměrem 2 × |KL|

Body K, L musí ležet uvnitř různých stran obdélníku. Strana AB leží na přímce a.

Zkusíme různé možnosti umístění obdélníku tak, aby:

AB ležela na přímce a
K, L byly uvnitř dvou různých stran
Jedna strana měla délku 2|KL|

Obvykle existují DVĚ řešení

3 Příklad 7.2: Co víme?

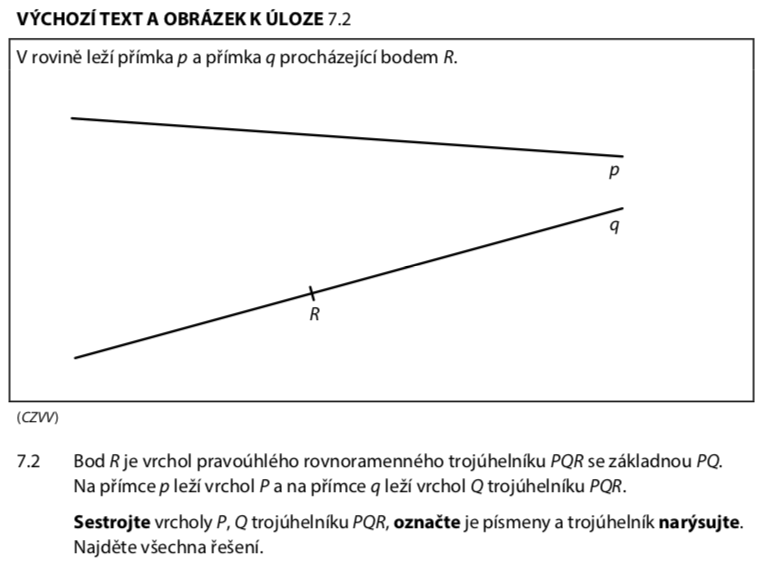
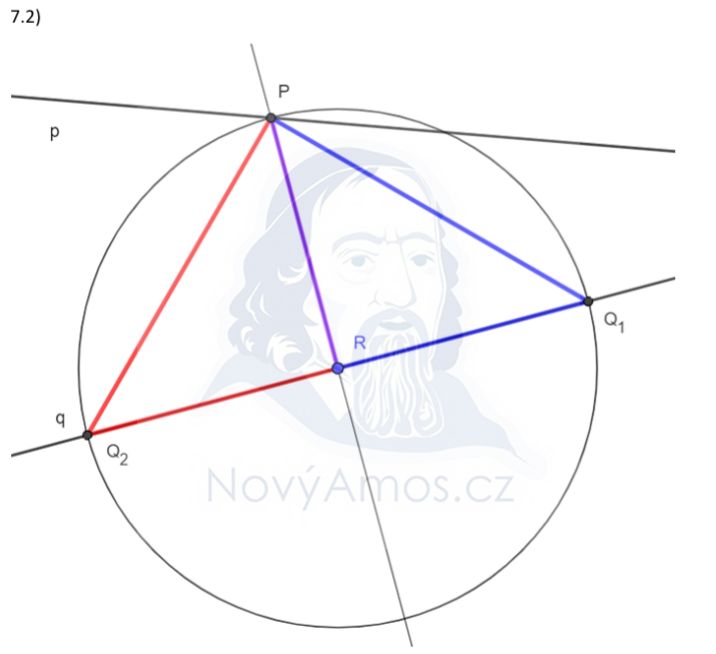
Přečteme si pozorně zadání:

Přímky p a q jsou dány, q prochází bodem R
Bod R je vrchol pravoúhlého trojúhelníku → v R je pravý úhel!
Trojúhelník je rovnoramenný → RP = RQ
Základna PQ → P leží na p, Q leží na q

4 Příklad 7.2: Thaletova kružnice

R je vrchol pravého úhlu. To znamená, že úhel PRQ = 90°.

Klíčová znalost: Bod R leží na Thaletově kružnici nad úsečkou PQ!

Všechny body na kružnici nad průměrem PQ vidí úsečku PQ pod pravým úhlem

Protože trojúhelník je rovnoramenný (RP = RQ), bod R leží na ose úsečky PQ.

5 Příklad 7.2: Sestrojíme trojúhelník

Postup:

Bod P leží na přímce p, bod Q leží na přímce q
Sestrojíme osu úsečky PQ (místo bodů stejně vzdálených od P a Q)
Bod R leží na průsečíku osy PQ a přímky q

Obvykle existují DVĚ řešení (R může být na dvou stranách PQ)

✅ Výsledek

7.1) Dva obdélníky ABCD

7.2) Dva trojúhelníky PQR

💡 Tip pro CERMAT

Pravoúhlý trojúhelník → Thaletova kružnice (vrchol pravého úhlu leží na kružnici nad přeponou)
Rovnoramenný trojúhelník → vrchol leží na ose základny
Kružnice s poloměrem 2|KL| ti pomůže najít správnou velikost obdélníku

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 7 (6 bodů)

7.1)

V rovině jsou dány body P, Q, R a přímka a. Na přímce a leží strana AB čtverce ABCD. Dva ze tří daných bodů leží uvnitř dvou různých stran čtverce ABCD a třetí z daných bodů leží vně čtverce ABCD. Sestrojte čtverec ABCD.

7.2)

V rovině je dána úsečka KL a bod U. Úsečka KL je strana trojúhelníku KLM. Jedna ze zbývajících stran má stejnou délku jako úsečka KL a druhá prochází bodem U. Sestrojte trojúhelník KLM.

1 Příklad 7.1: Co víme?

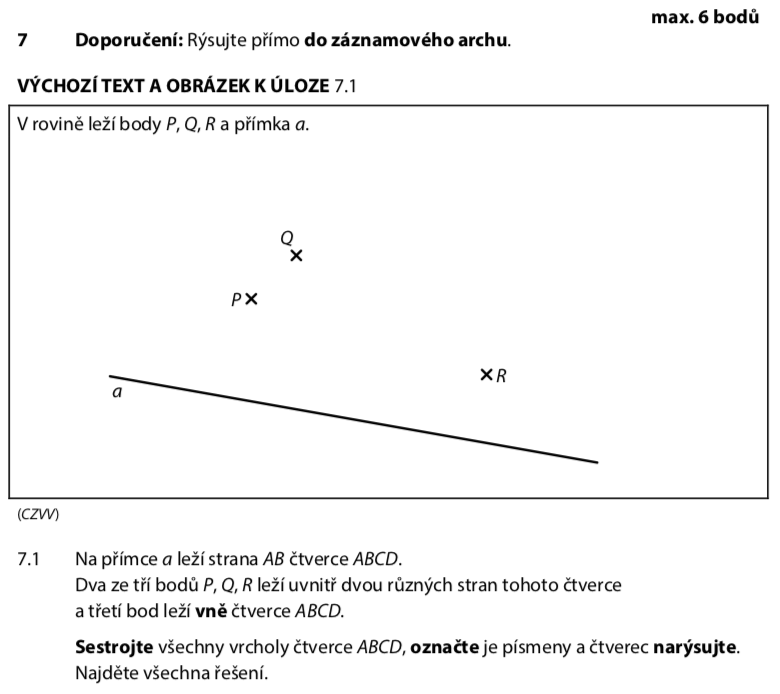
Přečteme si pozorně podmínky:

Body P, Q, R jsou dány
Přímka a je daná
Strana AB leží na přímce a
Dva body uvnitř různých stran, třetí vně čtverce → klíčová informace!

2 Příklad 7.1: Velikost čtverce

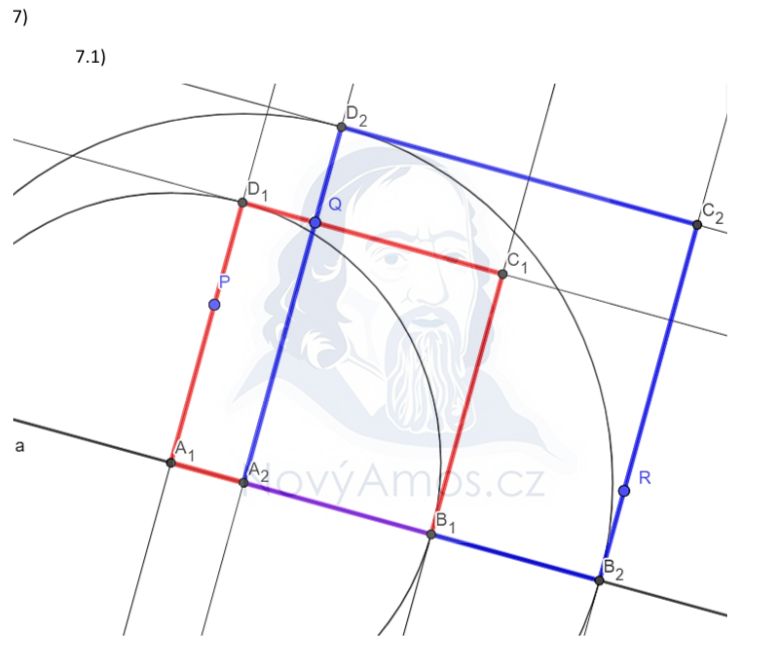
Bod, který leží vně čtverce, nám pomůže určit velikost čtverce.

Dva body uvnitř různých stran omezují minimální velikost čtverce.

Strana AB leží na přímce a

Zkusíme různé velikosti čtverce tak, aby:

AB ležela na přímce a
Dva body (např. P, Q) byly uvnitř dvou různých stran
Třetí bod (např. R) ležel vně čtverce

Obvykle existují DVĚ řešení (různé polohy čtverce na přímce a)

3 Příklad 7.2: Co víme?

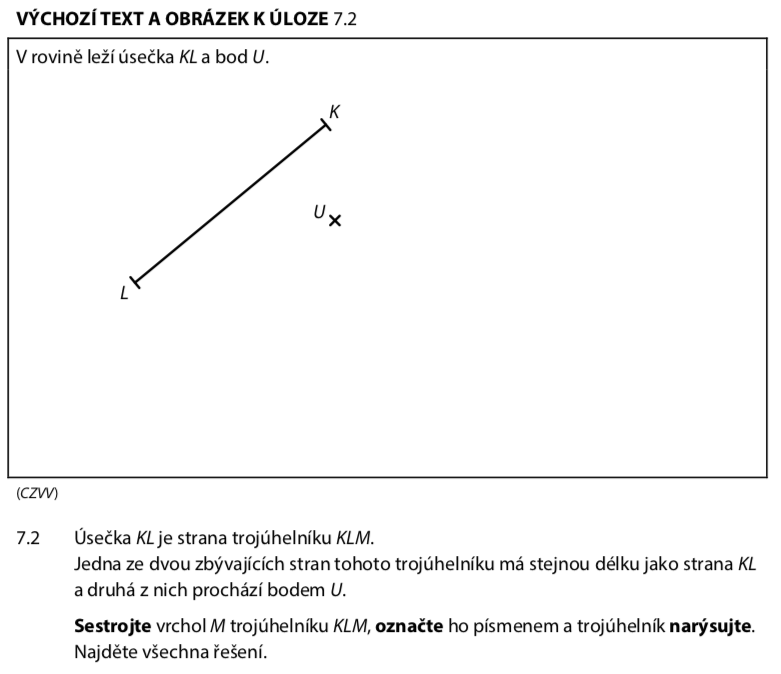
Přečteme si pozorně zadání:

Úsečka KL je daná (strana trojúhelníku)
Bod U je daný
Jedna ze zbývajících stran má stejnou délku jako KL → KM = |KL| nebo LM = |KL|
Druhá strana prochází bodem U

4 Příklad 7.2: První řešení (KM = |KL|)

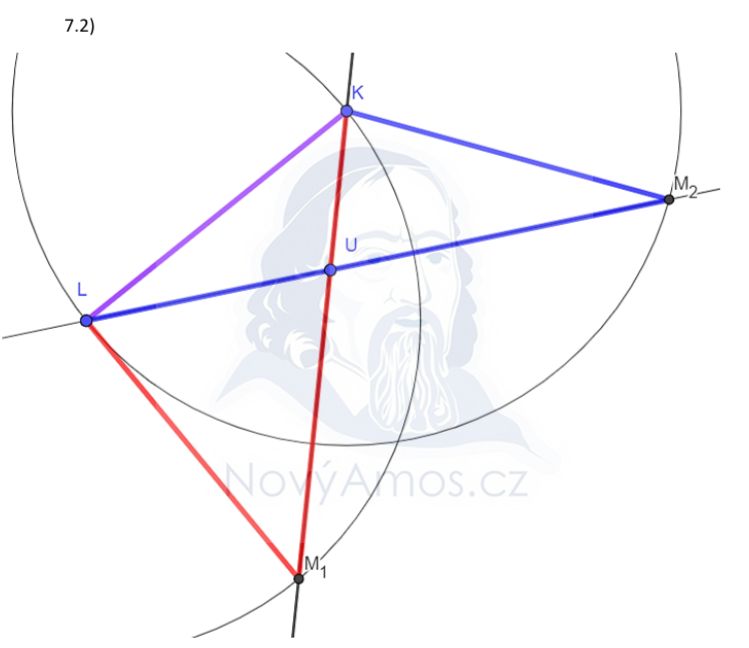
Zkusíme KM = |KL|. To znamená, že bod M má od K vzdálenost |KL|.

Sestrojíme kružnici se středem K a poloměrem |KL|

Zároveň víme, že strana LM prochází bodem U.

Vedeme přímku z L přes U

Průsečík této přímky s kružnicí je bod M₁. ✅

5 Příklad 7.2: Druhé řešení (LM = |KL|)

Zkusíme LM = |KL|. To znamená, že bod M má od L vzdálenost |KL|.

Sestrojíme kružnici se středem L a poloměrem |KL|

Zároveň víme, že strana KM prochází bodem U.

Vedeme přímku z K přes U

Průsečík této přímky s kružnicí je bod M₂. ✅

Máme DVĚ řešení: trojúhelníky KLM₁ a KLM₂

✅ Výsledek

7.1) Dva čtverce ABCD

7.2) Dva trojúhelníky KLM

💡 Tip pro CERMAT

Bod vně útvaru ti pomůže určit velikost útvaru
Kružnice najde bod ve správné vzdálenosti
U trojúhelníku s jednou stranou známou a jednou stranou stejně dlouhou: kružnice + přímka přes daný bod

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Geometrické konstrukce

Co si odnést z tohoto tématu

🧭 Strategie řešení

Přečti si VŠECHNY podmínky — podtrhni klíčová slova (rovnoběžná, kolmá, střed, rovnoramenný...)
Začni tím, co znáš — daný bod, přímka, úsečka
Nástroje konstrukce: rovnoběžka, kolmice, kružnice
Hledej VŠECHNA řešení — většinou jsou 2! (kružnice protne přímku ve 2 bodech)

⚠️ Typické chytáky

Zapomenout na druhé řešení — kružnice obvykle protne přímku ve dvou bodech
S je STŘED strany — musíš najít souměrný bod podle S
Kolmice ke špatné přímce — pozor, na jakou přímku má být kolmá!
Rovnoramenný trojúhelník — která dvě ramena jsou stejně dlouhá? (AB = AC nebo AB = BC?)

❌ Nejčastější chyby

Nepřesné rýsování — špatné průsečíky, nepřesná kolmice
Najít jen jedno řešení — CERMAT chce VŠECHNA řešení!
Nepoužít kružnici u rovnoramenného trojúhelníku — kružnice ti najde bod ve správné vzdálenosti
Zapomenout podmínku — např. „strana AB leží na přímce a"

📏 Geometrické konstrukce

🔑 Postup konstrukce

🎯 Rady pro CERMAT: Geometrické konstrukce