Logické úlohy | CERMAT 2023

📋 Zadání — 1. řádný termín, Úloha 3 (3 body)

Rota má jednoho kapitána. Kapitán má 4 poručíky. Každý poručík má 3 četaře. Každý četař má 10 vojínů. Kapitán vydal rozkaz, který se předával postupně: kapitán → poručíci → četaři → vojíni.

3.1) Kolik je v rotě vojínů?

3.2) Kolik osob rozkaz vydalo?

3.3) Kolik osob rozkaz přijalo?

1 Nakreslíme si hierarchii

Uspořádáme si všechny osoby podle toho, kdo má koho pod sebou:

1 kapitán
↓
4 poručíci
↓
? četaři
↓
? vojíni

2 Počet četařů

Každý poručík má 3 četaře. Poručíků je 4:

4 · 3 = 12 četařů

Celkem je v rotě 12 četařů.

3 Počet vojínů (3.1)

Každý četař má 10 vojínů. Četařů je 12:

12 · 10 = 120 vojínů

Odpověď na 3.1: 120 vojínů.

4 Kdo rozkaz vydal? (3.2)

Rozkaz vydali ti, kdo ho předali někomu dalšímu:

Kapitán (předal poručíkům)
4 poručíci (předali četařům)
12 četařů (předali vojínům)

1 + 4 + 12 = 17 osob

Odpověď na 3.2: 17 osob rozkaz vydalo.

5 Kdo rozkaz přijal? (3.3)

Rozkaz přijali všichni kromě kapitána (ten ho nevzal od nikoho, jen ho vydal):

4 poručíci (od kapitána)
12 četaři (od poručíků)
120 vojínů (od četařů)

4 + 12 + 120 = 136 osob

✅ Výsledek

3.1) 120 vojínů 3.2) 17 osob 3.3) 136 osob

💡 Tip pro CERMAT

U hierarchických úloh si nakresli schéma. Pozor na rozdíl:

Vydal = předal někomu dalšímu (nemá vojíny pod sebou)
Přijal = dostal od někoho (nemá nikoho nad sebou)

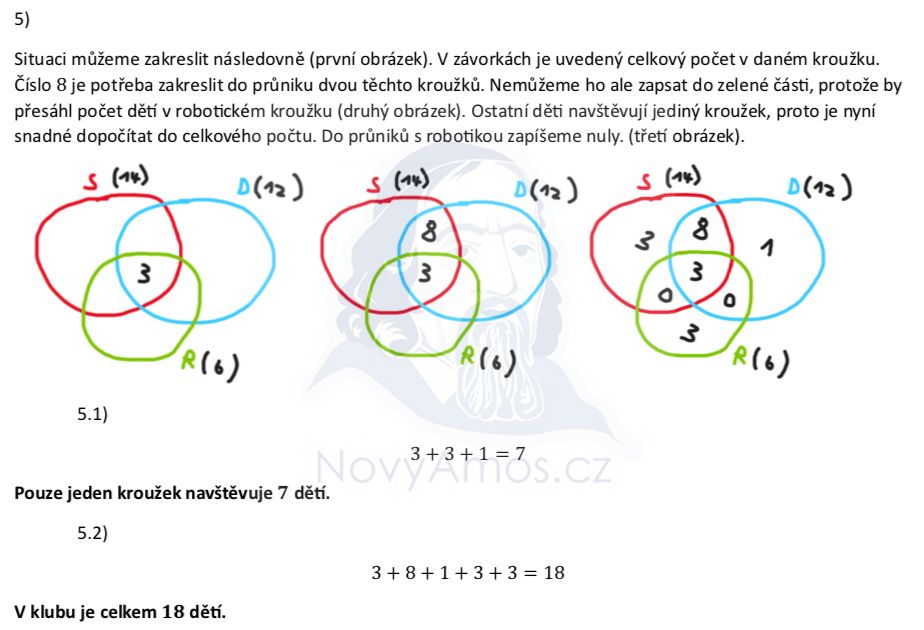
📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 5 (4 body)

V klubu SEN probíhají tři kroužky: sportovní (14 dětí), divadelní (12 dětí) a robotický (6 dětí). Právě 3 děti navštěvují všechny tři kroužky. Právě 8 dětí navštěvuje právě dva kroužky. Ostatní děti navštěvují právě jeden kroužek.

5.1) Kolik dětí navštěvuje právě jeden kroužek?

5.2) Kolik dětí navštěvuje klub SEN?

1 Vennův diagram: začínáme od průniku

Nakreslíme si tři kroužky (S = sportovní, D = divadelní, R = robotický). Do prostředka dáme ty, co chodí všude:

Všechny tři kroužky: 3 děti

Tuhle trojku si musíme pamatovat — je součástí všech tří kroužků!

2 Právě dva kroužky

Máme celkem 8 dětí v právě dvou kroužcích. Kde je dát?

Robotický kroužek má jen 6 dětí celkem. Z toho už 3 chodí všude. Kdyby další děti chodily do S∩R nebo D∩R, překročili bychom 6!

Všech 8 dětí musí být v průniku S∩D (sportovní a divadelní).

S ∩ D: 8 dětí

S ∩ R: 0 dětí

D ∩ R: 0 dětí

3 Pouze jeden kroužek

Nyní spočítáme, kolik dětí chodí jen do jednoho kroužku:

Sportovní celkem: 14

Všechny tři: 3, S∩D: 8 → pouze S: 14 − 3 − 8 = 3

Divadelní celkem: 12

Všechny tři: 3, S∩D: 8 → pouze D: 12 − 3 − 8 = 1

Robotický celkem: 6

Všechny tři: 3 → pouze R: 6 − 3 = 3

4 Sečteme výsledky

5.1) Jen jeden kroužek:

3 (jen S) + 1 (jen D) + 3 (jen R) = 7 dětí

5.2) Všechny děti celkem:

3 (všechny tři) + 8 (právě dva) + 7 (právě jeden) = 18 dětí

✅ Výsledek

5.1) 7 dětí 5.2) 18 dětí

⚠️ CERMAT chyták

Pozor na slovo „právě"! „Právě dva kroužky" znamená, že ty děti NEchodí všude. Děti „všechny tři" se nepočítají do „právě dva".

U Vennových diagramů vždy začni od průniku všech tří, pak průniky dvojic, nakonec „pouze jeden".

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 3 (4 body)

Palindromická čísla se čtou stejně zleva i zprava (např. 73937).

3.1) Jaké je nejmenší pěticiferné palindromické číslo s třemi různými číslicemi?

3.2) Kolik palindromických čísel je mezi čísly 34643 a 35253?

3.3) Jaké nejmenší číslo přičteme k 73937, abychom dostali palindromické číslo?

1 3.1: Nejmenší pěticiferné

Palindrom má tvar: ABCBA (první = páté, druhé = čtvrté).

Chceme nejmenší a máme použít tři různé číslice. Nejmenší jsou: 0, 1, 2.

Pozor! První číslice nemůže být 0 (pak by to nebylo pěticiferné číslo).

Nejmenší = 10201

(První a pátá = 1, druhá a čtvrtá = 0, prostřední = 2)

2 3.2: Mezi 34643 a 35253

Palindromy mezi těmito čísly mají tvar 34X43 nebo 35X53.

U tvaru 34X43 můžeme měnit prostřední číslici X:

34743,   34843,   34943   (3 palindromy)

U tvaru 35X53:

35053, 35153 (2 palindromy)

35253 už nepatří do intervalu (je konec).

Celkem: 3 + 2 = 5 palindromů

3 3.3: Nejbližší palindrom za 73937

Hledáme nejmenší palindrom větší než 73937.

Zkusíme tvar 7XXX7. Prostřední trojice musí být stejná zleva i zprava:

73937 → zkusíme 73937? Ne! (druhá a čtvrtá se neshodují)

Musíme zvýšit střed. Další palindrom:

74047

Rozdíl: 74047 − 73937 = 110

✅ Výsledek

3.1) 10201 3.2) 5 3.3) 110

💡 Tip pro CERMAT

U palindromů: první číslice nemůže být 0
Když hledáš další palindrom, zvyšuj prostřední číslici, pak druhou/čtvrtou
Pozor na hranice intervalu: „mezi" = nezahrnuje krajní čísla!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 5 (3 body)

Šest kamarádů vytvořilo všechny možné pětičlenné skupiny a všechny možné dvoučlenné skupiny.

5.1) Kolik pětičlenných skupin vytvořili?

5.2) Kolik dvoučlenných skupin vytvořili?

1 5.1: Pětičlenné skupiny

Máme 6 kamarádů. V pětičlenné skupině vždy chybí právě jeden.

Můžeme vybrat, kdo chybí:

Chybí A → skupina B,C,D,E,F

Chybí B → skupina A,C,D,E,F

Chybí C → skupina A,B,D,E,F

Chybí D → skupina A,B,C,E,F

Chybí E → skupina A,B,C,D,F

Chybí F → skupina A,B,C,D,E

Celkem: 6 pětičlenných skupin

2 5.2: Dvoučlenné skupiny — první pokus

Každý kamarád si může udělat dvojici s 5 dalšími:

6 · 5 = 30

Ale pozor! Tohle počítá každou dvojici dvakrát:

A-B je stejné jako B-A

C-D je stejné jako D-C

...

3 5.2: Oprava — dělíme dvěma

Každou dvojici jsme spočítali dvakrát. Musíme výsledek vydělit 2:

30 : 2 = 15 dvoučlenných skupin

Toto je typický vzorec pro kombinace: „ze 6 vybíráme 2" = 6·5 : 2 = 15.

✅ Výsledek

5.1) 6 skupin 5.2) 15 skupin

💡 Tip pro CERMAT

Kombinatorika: Když na pořadí nezáleží (dvojice A-B = B-A), musíš vydělit 2!

Vzorec: „ze 6 vybíráme 2" = 6 · 5 : 2 = 15

U pětičlenných skupin z 6 osob je to jednodušší: vždy jeden chybí → 6 skupin.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 9 (2 body)

Bytosti na planetě Zorstar mají 3 nohy a buď 3 nebo 4 oči. Několik bytostí má celkem 84 nohou. Tříokých bytostí je o 8 více než čtyřokých. Kolik očí mají tyto bytosti celkem?

Možnosti:

A) 94 B) 96 C) 102 D) 122 E) 130

1 Kolik je bytostí?

Každá bytost má 3 nohy. Celkem je 84 nohou:

84 : 3 = 28 bytostí

Na planetě je celkem 28 bytostí.

2 Rozdělení bytostí podle očí

Tříokých je o 8 více než čtyřokých. Kdybychom je měli půl napůl, bylo by jich po 14.

Ale tříokých je více! Musíme jeden typ zvýšit o 4, druhý snížit o 4:

Tříokých: 14 + 4 = 18

Čtyřokých: 14 − 4 = 10

Ověření: 18 − 10 = 8 ✅

3 Celkový počet očí

Spočítáme oči u každého typu a sečteme:

Tříoké: 18 · 3 = 54 očí

Čtyřoké: 10 · 4 = 40 očí

Celkem: 54 + 40 = 94 očí

✅ Výsledek

Odpověď: A) 94 očí

💡 Tip pro CERMAT

Úloha typu „kuřata a králíci":

1. Spočítej celkem (84:3 = 28 bytostí)
2. Udělej si průměr (28:2 = 14 a 14)
3. Posuň podle rozdílu (rozdíl 8 → +4 a −4)

📝 Oficiální řešení CERMAT

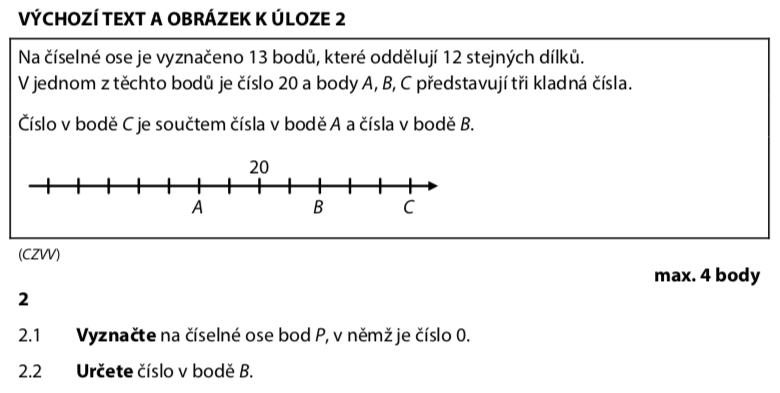
📋 Zadání — 2. náhradní termín, Úloha 2 (4 body)

Na číselné ose je 13 bodů — 12 stejných dílků. Jeden z bodů má číslo 20. Body A, B, C mají kladná čísla. Platí: C = A + B.

2.1) V jakém vztahu k bodu A je bod P s číslem 0?

2.2) Jaké číslo je v bodě B?

1 Najdeme vztah mezi A, B a C

Z obrázku vidíme, že bod s číslem 20 je mezi A a B.

Od A k bodu 20 jsou 2 dílky doprava, od 20 k B také 2 dílky doprava.

A = 20 − 2 dílky

B = 20 + 2 dílky

2 Použijeme podmínku C = A + B

Víme, že C = A + B:

C = (20 − 2d) + (20 + 2d) = 40

(d = velikost dílku)

Bod C má číslo 40. Z obrázku vidíme, že od bodu 20 k C je 5 dílků:

40 − 20 = 20 = 5 · d → d = 4

Jeden dílek = 4.

3 Najdeme B (2.2)

Bod B je 2 dílky vpravo od 20:

B = 20 + 2 · 4 = 28

4 Najdeme bod P (2.1)

Bod A je 2 dílky vlevo od 20:

A = 20 − 2 · 4 = 12

Bod P má číslo 0. Z obrázku vidíme, že P je vlevo od A:

12 − 0 = 12 = 3 · 4

Bod P je 3 dílky vlevo od A.

✅ Výsledek

2.1) P je 3 dílky vlevo od A 2.2) B = 28

💡 Tip pro CERMAT

U číselné osy:

Najdi vztah mezi body pomocí dílků (např. A = 20−2d, B = 20+2d)
Použij danou podmínku (C = A + B) k výpočtu velikosti dílku
Potom dopočítej všechny body

📝 Oficiální řešení CERMAT

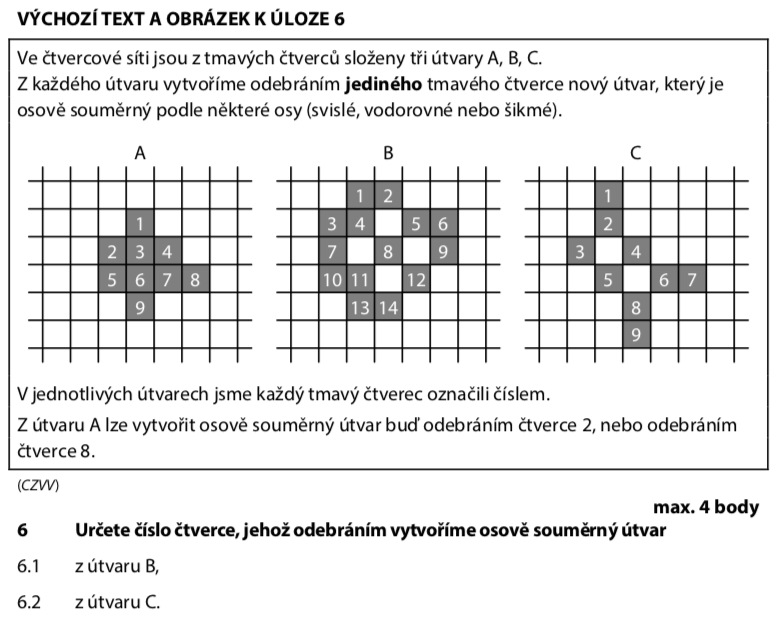
📋 Zadání — 2. náhradní termín, Úloha 6 (4 body)

Tři útvary A, B, C jsou složené z tmavých čtverců ve čtvercové síti. Z každého útvaru odebereme právě jeden čtverec tak, aby vznikl osově souměrný útvar.

Z útvaru A: odebrat čtverec 2 nebo 8.

6.1) Z útvaru B: odebrat čtverec?

6.2) Z útvaru C: odebrat čtverec?

1 Co je osová souměrnost?

Útvar je osově souměrný, když ho můžeš překlopit podle nějaké osy a obě půlky jsou stejné.

Osa může být svislá, vodorovná nebo šikmá.

Útvar A:

Odebereme-li čtverec 2 nebo 8, vznikne útvar se svislou osou souměrnosti uprostřed.

2 Útvar B (6.1)

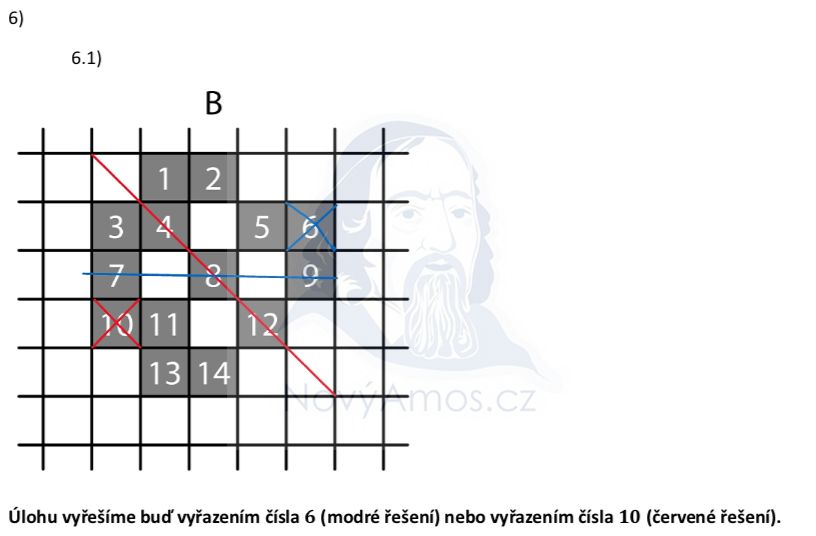
Podíváme se na útvar B. Zkusíme najít možné osy souměrnosti:

Odebráním čtverce 6: vznikne útvar se svislou osou souměrnosti

Odebráním čtverce 10: vznikne útvar se svislou osou souměrnosti

Odpověď: čtverec 6 nebo 10

3 Útvar C (6.2)

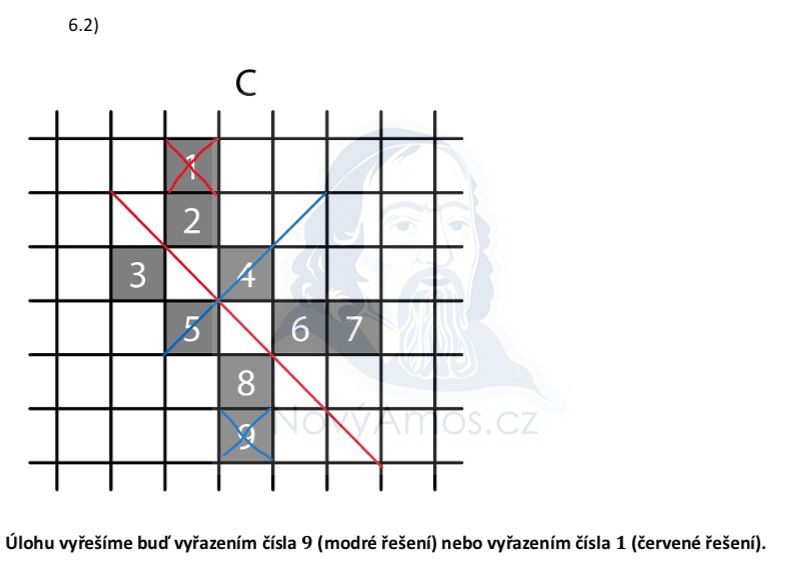
U útvaru C hledáme čtverec, jehož odebráním vznikne osově souměrný útvar:

Pozor! Zkus i šikmou osu (úhlopříčku)!

Odebráním čtverce 9: vznikne útvar se šikmou osou souměrnosti

Odebráním čtverce 1: vznikne útvar se šikmou osou souměrnosti

Odpověď: čtverec 9 nebo 1

✅ Výsledek

6.1) čtverec 6 nebo 10 6.2) čtverec 9 nebo 1

⚠️ CERMAT chyták

U osové souměrnosti nezapomeň zkusit i šikmou osu (úhlopříčku)!

Užitečný trik: zkus si útvar „překlopit" podle různých os a podívej se, jestli obě půlky pasují.

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Logické úlohy

Co si odnést z tohoto tématu

🧭 Strategie řešení

Vennovy diagramy: Vždy začni od průniku všech tří, pak průniky dvojic, nakonec „pouze jeden"
Palindromy: Když hledáš další, zvyšuj prostřední číslici, pak druhou/čtvrtou
Kombinatorika: „Ze 6 vybíráme 2" = 6 · 5 : 2 (když na pořadí nezáleží)
Hierarchie: Nakresli si schéma, rozlišuj „vydal" vs. „přijal"

⚠️ Typické chytáky

Průnik tří kroužků se počítá do všech tří (nesmíš ho počítat znovu do dvojic!)
U palindromů: první číslice nemůže být 0
U kombinací: když na pořadí nezáleží, děl 2 (A-B = B-A)
U osové souměrnosti: nezapomeň zkusit i šikmou osu!

❌ Nejčastější chyby

Zapomenout dělit 2 u kombinací (když pořadí nezáleží)
Přehlédnout šikmou osu souměrnosti
U úlohy „kuřata a králíci": špatný výchozí průměr (zapomenout vydělit 2)
U Vennových diagramů: počítat průnik tří znovu do dvojic

🧠 Logické úlohy

🔑 Logické myšlení

🎯 Rady pro CERMAT: Logické úlohy