Vzory a posloupnosti | CERMAT 2023

📋 Zadání — 1. řádný termín, Úloha 14 (4 body)

Ze světlých a tmavých čtverečků tvoříme obrazce tvaru čtverce nebo obdélníku. Základní obrazec tvoří řady světlých čtverečků. Rozšířený obrazec vznikne tak, že k základnímu obrazci přidáme nahoře řadu tmavých čtverečků a vlevo i vpravo sloupec tmavých čtverečků.

14.1) Základní obrazec má 5 řad světlých čtverečků. Do rozšířeného obrazce jsme přidali 30 tmavých čtverečků. Kolik sloupců má rozšířený obrazec?

14.2) Rozšířený obrazec má 3 řady a stejný počet tmavých a světlých čtverečků. Kolik sloupců má tento rozšířený obrazec?

14.3) Kolik rozšířených obrazců můžeme vytvořit tak, že použijeme právě 50 tmavých čtverečků?

1 Rozkoukáme, jak roste obrazec

Základní obrazec = obdélník ze světlých čtverečků. Rozšířený obrazec = přidáme tmavé čtverečky:

Nahoře řada tmavých čtverečků (podle počtu sloupců)
Vlevo sloupec tmavých (podle počtu řad)
Vpravo sloupec tmavých (podle počtu řad)
Plus 2 rohy (vlevo nahoře, vpravo nahoře)

Počet tmavých = počet_sloupců + 2 · počet_řad + 2

2 Úloha 14.1: Dopočítáme sloupce

Víme: 5 řad, 30 tmavých čtverečků. Dosadíme do vzorce:

30 = počet_sloupců + 2 · 5 + 2

30 = počet_sloupců + 10 + 2

30 = počet_sloupců + 12

počet_sloupců = 18

3 Úloha 14.2: Stejně světlých i tmavých

Rozšířený má 3 řady. Základní měl jen 2 řady (rozšířený = základní + 1 řada nahoře).

Světlé čtverečky: základní obrazec má 2 · počet_sloupců

Tmavé čtverečky:

počet_sloupců + 2 · 2 + 2 = počet_sloupců + 6

Podmínka: stejný počet světlých a tmavých:

2 · počet_sloupců = počet_sloupců + 6

počet_sloupců = 6

Rozšířený obrazec má o 2 sloupce více (rohy): 6 + 2 = 8 sloupců

4 Úloha 14.3: Kolik různých obrazců?

Máme 50 tmavých čtverečků. Hledáme, kolik různých kombinací (počet_řad, počet_sloupců) splní:

počet_sloupců + 2 · počet_řad + 2 = 50

počet_sloupců + 2 · počet_řad = 48

Počet řad musí být aspoň 1. Počet sloupců musí být kladný:

počet_sloupců = 48 − 2 · počet_řad > 0

48 − 2 · počet_řad > 0 → počet_řad < 24

Počet řad může být 1, 2, 3, ..., 23. To je celkem 23 různých obrazců.

✅ Výsledek

14.1) 18 sloupců 14.2) 8 sloupců 14.3) 23 obrazců

💡 Tip pro CERMAT

U úloh s obrazci:

Napřed si napiš vzoreček (kolik čtverečků kde je)
Pozor na rohy — ty se často zapomínají nebo počítají 2×
U 14.3 si promysli: kdy je počet sloupců větší než 0?

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 14 (4 body)

Obdélníky skládáme z bílých a šedých čtverečků. Delší strana obdélníku je vždy 2× delší než kratší strana. Bílé čtverečky: 1·1, 2·3, 3·5, 4·7, ... (n-tý obdélník má bílých n·(2n−1)). Šedé čtverečky jsou v n řadách po (2n) čtverečcích.

14.1) Kolik čtverečků má celkem 4. obdélník?

14.2) V obdélníku je 45 bílých čtverečků. Kolik je v něm šedých čtverečků?

14.3) V obdélníku je o 7 bílých čtverečků více než šedých. Kolik je v něm bílých čtverečků?

1 Nakreslíme si tabulku prvních obrazců

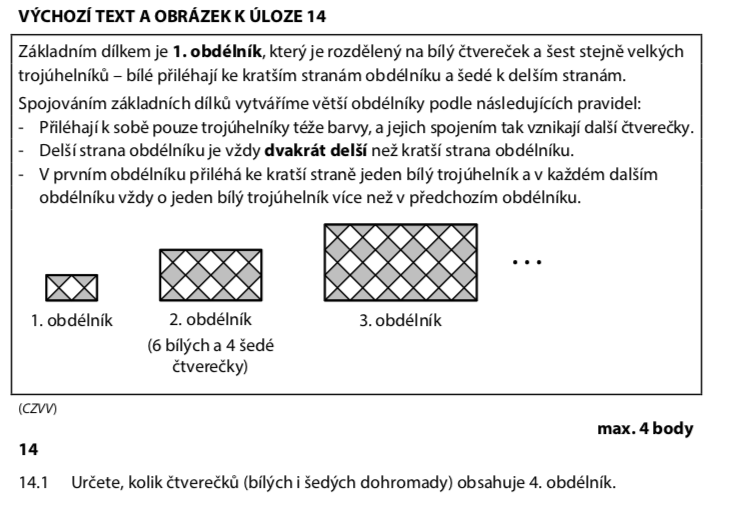
Pojďme si zapsat první obrazce, abychom viděli pravidlo:

Obrazec č.	Bílé čtverečky	Šedé čtverečky
1	1 · 1 = 1	0 · 2 = 0
2	2 · 3 = 6	1 · 4 = 4
3	3 · 5 = 15	2 · 6 = 12
4	4 · 7 = 28	3 · 8 = 24

Vzorce: Bílé = n · (2n − 1), šedé = (n − 1) · 2n

2 Úloha 14.1: Celkem čtverečků ve 4. obdélníku

Ze tabulky vidíme:

Bílé = 4 · 7 = 28

Šedé = 3 · 8 = 24

Celkem = 28 + 24 = 52

3 Úloha 14.2: Z 45 bílých dopočítat šedé

Hledáme n takové, že n · (2n − 1) = 45:

1 · 1 = 1, 2 · 3 = 6, 3 · 5 = 15, 4 · 7 = 28, 5 · 9 = 45

Je to 5. obrazec (n = 5). Šedé čtverečky:

(5 − 1) · (2 · 5) = 4 · 10 = 40

4 Úloha 14.3: Rozdíl bílých a šedých je 7

Podívejme se na rozdíly (bílé − šedé):

Obrazec č.	Bílé	Šedé	Rozdíl
1	1	0	1
2	6	4	2
3	15	12	3
4	28	24	4

Rozdíl roste vždy o 1! U 7. obrazce bude rozdíl 7.

Bílé = 7 · (2 · 7 − 1) = 7 · 13 = 91

✅ Výsledek

14.1) 52 14.2) 40 šedých 14.3) 91 bílých

💡 Tip pro CERMAT

Když vidíš nějakou složitější posloupnost:

Zapiš si ji do tabulky (prvních 4–5 hodnot)
Hledej, jak roste rozdíl mezi sousedními členy
Pokud rozdíl roste pravidelně (o 1, o 2, ...), je to součin po sobě jdoucích čísel

📝 Oficiální řešení CERMAT

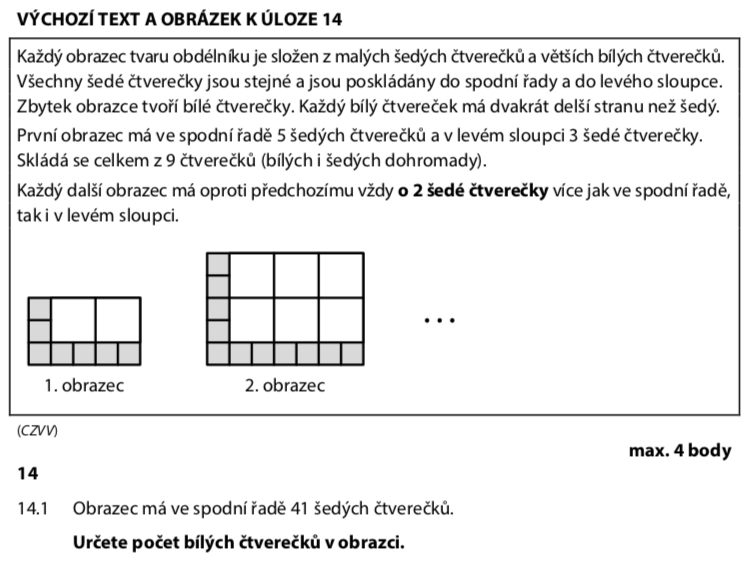
📋 Zadání — 1. náhradní termín, Úloha 14 (4 body)

Obdélníky skládáme z šedých (spodní řada + levý sloupec) a bílých čtverečků (větší obdélník, 2× delší strana). Každý další obdélník má +2 šedé ve spodní řadě i levém sloupci.

14.1) Spodní řada má 41 šedých čtverečků. Kolik je v obdélníku bílých čtverečků?

14.2) V obdélníku je 90 bílých čtverečků. Kolik je v něm šedých čtverečků?

14.3) Poslední obdélník má o 106 čtverečků více než předposlední. Kolik je v posledním obdélníku šedých čtverečků?

1 Rozkoukáme pravidlo růstu

Zakreslíme si, jak obrazec roste:

Spodní řada má lichý počet šedých (3, 5, 7, 9, ...)
Levý sloupec má vždy o 1 méně (2, 4, 6, 8, ...)
Jeden roh se počítá 2× → odečteme 1

Pokud má spodní řada s šedých a levý sloupec s−1 šedých:

Šedé = s + (s − 1) − 1 = 2s − 2

Bílých: (s − 2) řad po (s − 1) čtverečcích:

Bílé = (s − 2) · (s − 1)

2 Úloha 14.1: Z 41 šedých v řadě dopočítat bílé

Spodní řada má 41 šedých → s = 41. Bílé:

(41 − 2) · (41 − 1) = 39 · 40 = 1560 ... chyba!

⚠️ Pozor, špatně jsme počítali!

Správně: Pokud spodní řada má 41 šedých, bílých je o 1 méně v řadě (40) a řad je o 2 méně (39, protože horní 2 rohy chybí).

Vzoreček: Bílé v řadě = (šedé_v_řadě − 1), řad = (šedé_v_řadě − 2)

(41 − 1) : 2 = 20 bílých v řadě

Bílé = 20 · 19 = 380

3 Úloha 14.2: Z 90 bílých dopočítat šedé

Hledáme, jaké dva po sobě jdoucí čísla dají součin 90:

8 · 9 = 72, 9 · 10 = 90

Bílé: 10 v řadě, 9 ve sloupci. Obdélník má tedy:

Spodní řada: 10 + 1 = 11 šedých
Levý sloupec: 9 + 1 = 10 šedých
Roh se počítá 2× → odečteme 1

Šedé = 2 · (10 + 9) + 1 = 2 · 19 + 1 = 39

4 Úloha 14.3: Rozdíl 106 mezi posledním a předposledním

Když rosteme o 1 obrazec, přidáme:

2 šedé ve spodní řadě (nový obrazec má +2 oproti předchozímu)
2 šedé v levém sloupci
Zbytek: nové bílé čtverečky

Celkem přidáme 106 čtverečků. Z toho 4 šedé, zbytek bílé:

106 − 4 = 102 bílých čtverečků

102 bílých = nová řada + nový sloupec. Řada má o 1 víc než sloupec:

(102 + 1) : 2 = 51,5... chyba!

⚠️ Správně:

Přidaná řada má stejně jako předchozí řada bílých + 1 navíc. Přidaný sloupec má stejně jako předchozí sloupec. Celkem: 102 = x + (x + 1), kde x je počet bílých ve sloupci.

Lépe: Přidaná horní řada má 52 bílých, levý sloupec 51 bílých (52 + 50 = 102).

Šedé = 2 · 52 + 2 · 51 + 1 = 104 + 102 + 1 = 207

✅ Výsledek

14.1) 380 bílých 14.2) 39 šedých 14.3) 207 šedých

⚠️ CERMAT chyták

U úlohy 14.3 je nejčastější chyba:

Zapomenout, že roh se sdílí (počítá se jen 1×)
Nesprávný rozklad 102 na součet (51,5 není celé číslo!)
Řešení: promysli si přesně, kolik čtverečků přidáváme do řady a kolik do sloupce

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 14 (4 body)

Trojúhelníkové obrazce z pater šedých trojúhelníků. Puntíky ve vrcholech, úsečky na stranách.

Patra	1	2	3
Trojúhelníky	1	3	6
Puntíky	3	6	10
Úsečky	3	9	18

14.1) Kolik úseček má obrazec s 5 patry?

14.2) Počet úseček v posledním a předposledním obrazci se liší o 96. O kolik se v těchto obrazcích liší počet puntíků?

14.3) Obrazec má 300 puntíků. Kolik úseček bude mít následující (větší) obrazec?

1 Hledáme pravidla růstu

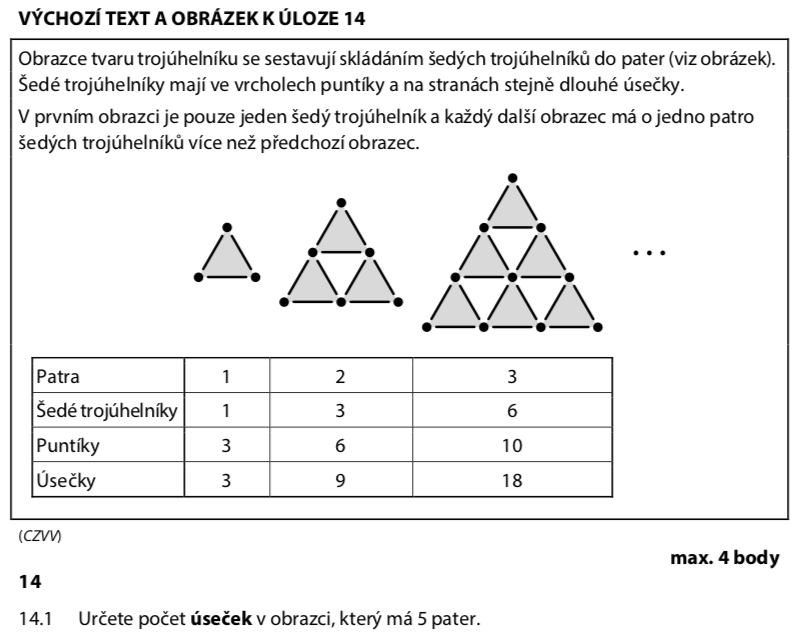
Rozšíříme tabulku a hledáme vzorec:

Patra (n)	Trojúhelníky	Puntíky	Úsečky
1	1	3	3 = 1 · 3
2	1 + 2 = 3	6	9 = 3 · 3
3	1 + 2 + 3 = 6	10	18 = 6 · 3
4	1 + 2 + 3 + 4 = 10	15	30 = 10 · 3
5	1 + 2 + 3 + 4 + 5 = 15	21	45 = 15 · 3

Vidíme: Úsečky = trojúhelníky · 3

A puntíky? Puntíky v n-patrovém = trojúhelníky v (n+1)-patrovém!

2 Úloha 14.1: Úsečky v 5patrovém

Trojúhelníky v 5patrovém:

1 + 2 + 3 + 4 + 5 = 15

Úsečky:

15 · 3 = 45

3 Úloha 14.2: Rozdíl úseček je 96

Rozdíl úseček = 96. Úsečky = trojúhelníky · 3, takže:

96 : 3 = 32 trojúhelníků

Poslední patro má 32 trojúhelníků → obrazec má 32 pater.

Puntíky se liší o počet puntíků v posledním patře, což je o 1 víc než počet pater:

32 + 1 = 33 puntíků

4 Úloha 14.3: Z 300 puntíků k úsečkám v následujícím

Puntíky v n-patrovém = trojúhelníky v (n+1)-patrovém. Máme 300 puntíků:

Trojúhelníky v následujícím = 300

Úsečky v následujícím:

300 · 3 = 900

✅ Výsledek

14.1) 45 úseček 14.2) o 33 puntíků 14.3) 900 úseček

💡 Tip pro CERMAT

Klíč k úspěchu:

Zapiš si tabulku prvních 4–5 hodnot
Hledej vzorec mezi sloupci (např. úsečky = trojúhelníky · 3)
Pozor na off-by-one chyby: puntíky v n-tém = trojúhelníky v (n+1)-ním!

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Vzory a posloupnosti

Co si odnést z tohoto tématu

🧭 Strategie řešení

Zapiš si první 3–4 členy posloupnosti do tabulky
Hledej pravidlo růstu: o kolik se liší sousední členy? (přírůstek)
Pokud přírůstek roste pravidelně → hledej součin nebo součet řady (1+2+3+...)
Ověř si pravidlo zpětně na známých hodnotách

⚠️ Typické chytáky

Záměna „n-tý obrazec" a „obrazec s n patry" — off-by-one chyba!
Sdílené prvky (rohy) — počítají se jen 1×, ne 2×
Součin po sobě jdoucích čísel (např. 9 · 10 = 90) — klasický CERMAT vzor

❌ Nejčastější chyby

Zapomenout na rohový čtvereček (počítat ho 2× nebo vůbec)
Chybný rozklad čísla na součin (např. hledat, jaké dvě čísla dají součin 90)
Neověřit si pravidlo na prvních členech (hned uvidíš, jestli funguje!)

🔄 Vzory a posloupnosti

🔑 Jak najít vzor v posloupnosti

🎯 Rady pro CERMAT: Vzory a posloupnosti