Čtení grafů a A/N tvrzení

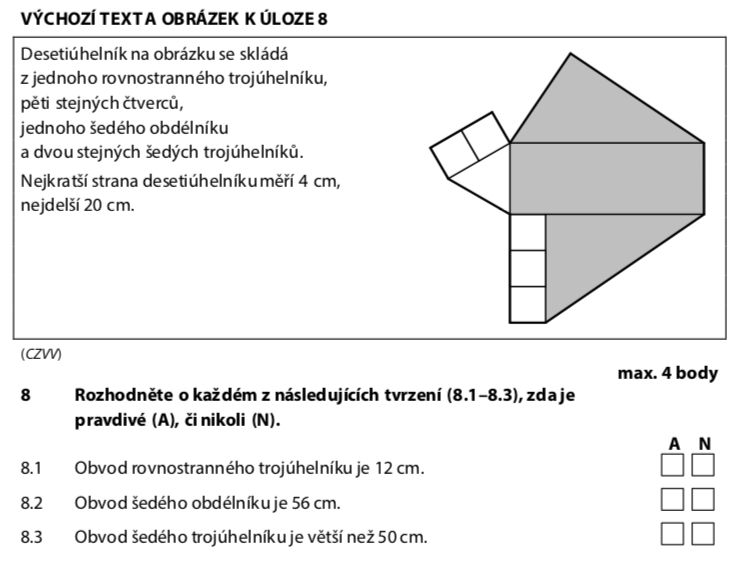
📋 Zadání — 1. řádný termín, Úloha 8 (4 body)

Desetiúhelník se skládá z rovnostranného trojúhelníku, pěti čtverců, šedého obdélníku a dvou šedých trojúhelníků. Nejkratší strana má délku 4 cm, nejdelší 20 cm.

8.1) Obvod rovnostranného trojúhelníku je 12 cm. (ANO / NE)

8.2) Obvod šedého obdélníku je 56 cm. (ANO / NE)

8.3) Obvod šedého trojúhelníku je větší než 50 cm. (ANO / NE)

1 Zjistíme stranu čtverce

Z obrázku vidíme, že nejkratší strana je 4 cm — to je strana čtverce.

Strana čtverce = 4 cm

Všechny čtverce mají stejnou stranu.

2 Tvrzení 8.1: Obvod rovnostranného trojúhelníku

Rovnostranný trojúhelník má stranu rovnou dvěma stranám čtverce:

Strana trojúhelníku = 2 · 4 = 8 cm

Obvod rovnostranného trojúhelníku:

3 · 8 = 24 cm

Tvrzení říká 12 cm → NE (nepravda)

3 Tvrzení 8.2: Obvod šedého obdélníku

Šedý obdélník má rozměry:

Šířka = 8 cm (strana rovnostranného trojúhelníku)

Délka = 20 cm (nejdelší strana)

Obvod obdélníku:

2 · (8 + 20) = 2 · 28 = 56 cm

Tvrzení říká 56 cm → ANO (pravda)

4 Tvrzení 8.3: Obvod šedého trojúhelníku

Šedý trojúhelník má strany:

12 cm, 20 cm, 16 cm

Obvod šedého trojúhelníku:

12 + 20 + 16 = 48 cm

Tvrzení říká větší než 50 cm → 48 < 50 → NE (nepravda)

✅ Výsledek

8.1) NE 8.2) ANO 8.3) NE

💡 Tip pro CERMAT

U geometrických úloh s obrázkem:

Najdi nejkratší stranu — často je to základ pro další výpočty
Pozor na porovnání: „větší než 50" znamená > 50 (ne = 50)
U obdélníku: obvod = 2·(a + b)

📝 Oficiální řešení CERMAT

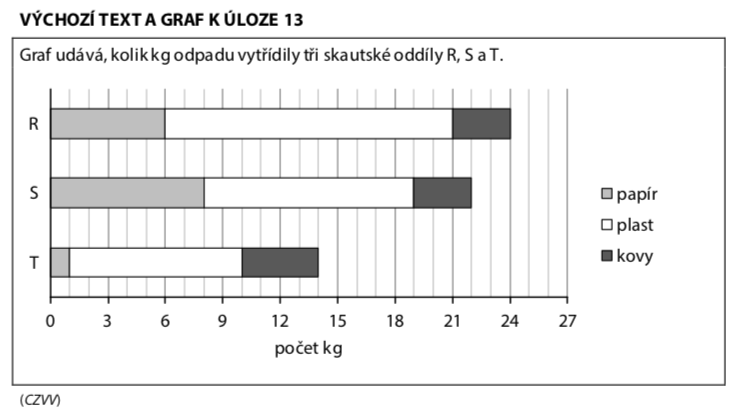
📋 Zadání — 1. řádný termín, Úloha 13 (5 bodů)

Graf udává, kolik kilogramů odpadu vytřídily oddíly R, S a T (papír, plast, kovy).

R: papír 6 kg, plast 15 kg, kovy 3 kg

S: papír 8 kg, plast 11 kg, kovy 3 kg

T: papír 1 kg, plast 9 kg, kovy 4 kg

13.1) Oddíl R vytřídil ... méně kilogramů papíru než oddíl S.

A) o šestinu B) o pětinu C) o čtvrtinu D) o třetinu E) o polovinu F) dvakrát

13.2) Oddíly S a T dohromady vytřídily ... více kilogramů plastu než oddíl R.

13.3) Všechny tři oddíly dohromady vytřídily ... více kilogramů papíru než kovů.

1 Tvrzení 13.1: Papír — R vs S

Z grafu:

R vytřídil papíru: 6 kg

S vytřídil papíru: 8 kg

Rozdíl:

8 − 6 = 2 kg

Kolik je 2 kg z 8 kg?

2 : 8 = 1 : 4 = čtvrtina

Oddíl R vytřídil o čtvrtinu méně než S → C

2 Tvrzení 13.2: Plast — S+T vs R

Z grafu:

S vytřídil plastu: 11 kg, T vytřídil: 9 kg

S + T = 11 + 9 = 20 kg

R vytřídil plastu: 15 kg

Rozdíl:

20 − 15 = 5 kg

Kolik je 5 kg z 15 kg?

5 : 15 = 1 : 3 = třetina

S+T vytřídily o třetinu více než R → D

3 Tvrzení 13.3: Papír vs kovy — celkem

Celkem papír:

6 + 8 + 1 = 15 kg

Celkem kovy:

3 + 3 + 4 = 10 kg

Rozdíl:

15 − 10 = 5 kg

Kolik je 5 kg z 10 kg?

5 : 10 = 1 : 2 = polovina

Vytřídily o polovinu více papíru než kovů → E

✅ Výsledek

13.1) → C 13.2) → D 13.3) → E

💡 Tip pro CERMAT

Při počítání „o kolik více/méně":

Spočítej rozdíl (větší − menší)
Vyděl rozdíl základem (číslem, se kterým srovnáváš)
Převeď zlomek: 1/2 = polovina, 1/3 = třetina, 1/4 = čtvrtina...

📝 Oficiální řešení CERMAT

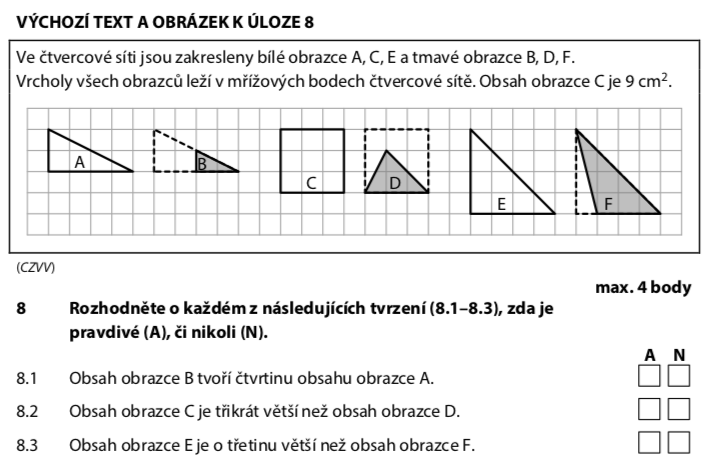
📋 Zadání — 2. řádný termín, Úloha 8 (4 body)

Ve čtvercové síti jsou znázorněny obrazce A, C, E (bílé) a B, D, F (tmavé). Obsah obrazce C je 9 cm².

8.1) Obsah obrazce B tvoří čtvrtinu obsahu obrazce A. (ANO / NE)

8.2) Obsah obrazce C je třikrát větší než obsah obrazce D. (ANO / NE)

8.3) Obsah obrazce E je o třetinu větší než obsah obrazce F. (ANO / NE)

1 Spočítáme obrazce ve čtverečcích

Z obrázku spočítáme, kolik čtverečků zabírá každý obrazec:

A = 4, B = 1, C = 9

D = 3, E = 8, F = 6

(v jednotkách čtverečků)

2 Tvrzení 8.1: B tvoří čtvrtinu A?

Čtvrtina obsahu A:

A = 4 → 1/4 · 4 = 1

Obsah B:

B = 1

B = 1/4 · A → ANO (pravda)

3 Tvrzení 8.2: C je třikrát větší než D?

Obsah D:

D = 3

Třikrát větší než D:

3 · 3 = 9

Obsah C = 9 → ANO (pravda)

4 Tvrzení 8.3: E je o třetinu větší než F?

Obsah F:

F = 6

O třetinu větší znamená:

Třetina z 6 = 6 : 3 = 2

F + třetina = 6 + 2 = 8

Obsah E = 8 → ANO (pravda)

✅ Výsledek

8.1) ANO 8.2) ANO 8.3) ANO

⚠️ CERMAT chyták

Pozor na rozdíl:

„Třikrát větší" = násobíme 3× (např. 3 · 3 = 9)
„O třetinu větší" = přidáme 1/3 (např. 6 + 6/3 = 8)

Toto je jeden z nejčastějších chytáků v testech CERMAT!

📝 Oficiální řešení CERMAT

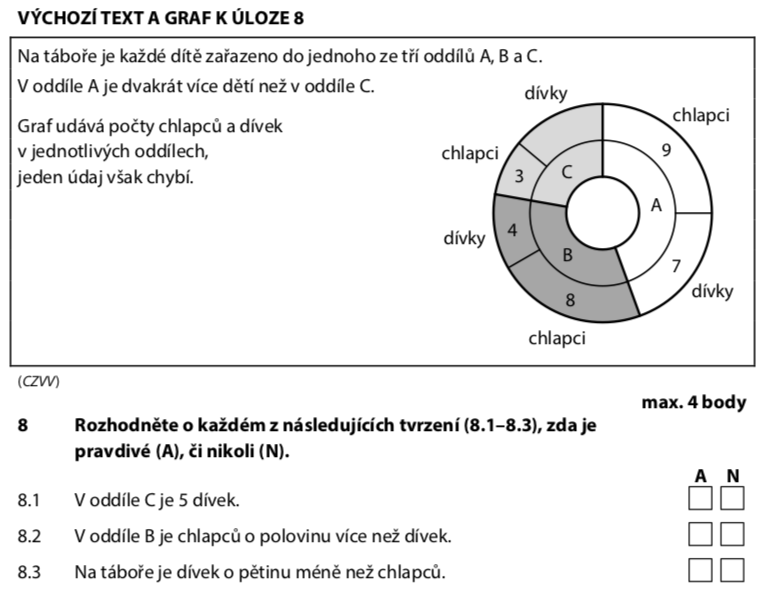
📋 Zadání — 1. náhradní termín, Úloha 8 (4 body)

Na táboře jsou oddíly A, B, C. V oddíle A je dvakrát více dětí než v oddíle C. Graf udává počty chlapců a dívek v jednotlivých oddílech, jeden údaj chybí.

Oddíl A: chlapci 9, dívky ?

Oddíl B: chlapci 8, dívky 4

Oddíl C: chlapci 3, dívky ?

8.1) V oddíle C je 5 dívek. (ANO / NE)

8.2) V oddíle B je chlapců o polovinu více než dívek. (ANO / NE)

8.3) Na táboře je dívek o pětinu méně než chlapců. (ANO / NE)

1 Dopočítáme chybějící údaje

Víme, že v A je 2× více dětí než v C. Zkusíme najít počty dívek:

C: chlapci 3 + dívky ?

A: chlapci 9 + dívky ?

Pokud jsou v A dívky 7 a v C dívky 5:

A = 9 + 7 = 16

C = 3 + 5 = 8

16 = 2 · 8 ✓ → Podmínka sedí!

2 Tvrzení 8.1: V C je 5 dívek?

Podle našeho výpočtu:

Dívky v C = 5

Tvrzení říká 5 dívek → ANO (pravda)

3 Tvrzení 8.2: V B je chlapců o polovinu více než dívek?

V oddíle B:

Chlapci = 8, Dívky = 4

O polovinu více než dívky znamená:

Polovina z 4 = 4 : 2 = 2

4 + 2 = 6

Ale chlapců je 8, ne 6 → NE (nepravda)

4 Tvrzení 8.3: Dívek o pětinu méně než chlapců?

Celkem:

Chlapci: 9 + 8 + 3 = 20

Dívky: 7 + 4 + 5 = 16

O pětinu méně než chlapců znamená:

Pětina z 20 = 20 : 5 = 4

20 − 4 = 16

Dívek je 16 → ANO (pravda)

✅ Výsledek

8.1) ANO 8.2) NE 8.3) ANO

💡 Tip pro CERMAT

Když graf obsahuje chybějící údaje:

Najdi další podmínku v zadání (zde: A = 2·C)
Zkus různé hodnoty a ověř podmínku
Teprve pak řeš jednotlivá tvrzení

📝 Oficiální řešení CERMAT

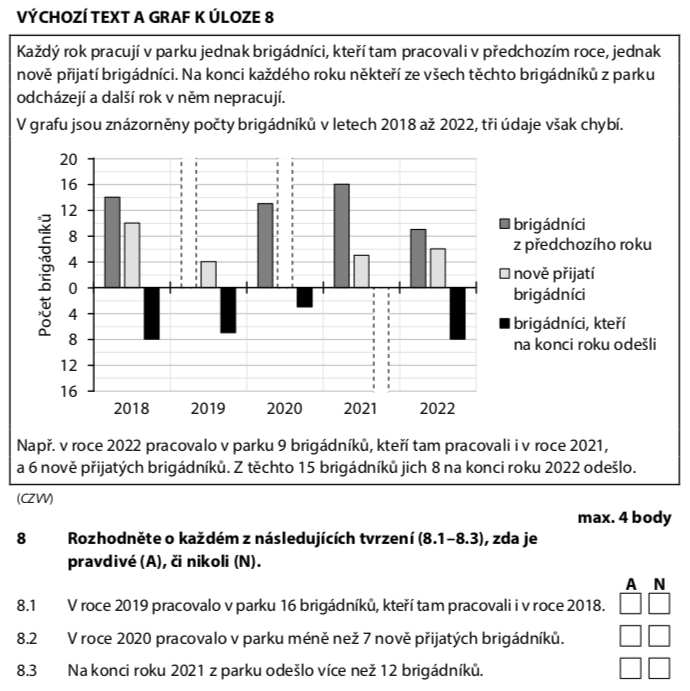
📋 Zadání — 2. náhradní termín, Úloha 8 (4 body)

V městském parku pracovali brigádníci v letech 2018–2022. Každý rok: brigádníci z předchozího roku + nově přijatí − odešlí. Graf obsahuje 3 chybějící údaje.

8.1) V roce 2019 pracovalo 16 brigádníků z předchozího roku. (ANO / NE)

8.2) V roce 2020 bylo méně než 7 nově přijatých brigádníků. (ANO / NE)

8.3) Na konci roku 2021 odešlo více než 12 brigádníků. (ANO / NE)

1 Tvrzení 8.1: Rok 2019

Rok 2018:

Z předchozího: 14, Nově: 10

Celkem: 14 + 10 = 24

Na konci 2018 odešlo 8:

Zůstalo do 2019: 24 − 8 = 16

V 2019 pracovalo 16 z předchozího roku → ANO (pravda)

2 Tvrzení 8.2: Rok 2020 — nově přijatí

Víme, že v 2020:

Z předchozího: 13, Odešli: 3

V 2021 pracovalo z předchozího roku 16 (z grafu). To znamená:

13 + nově − 3 = 16

13 + nově = 19

Nově = 6

Je 6 < 7? ANO → ANO (pravda)

3 Tvrzení 8.3: Konec roku 2021

V 2021:

Z předchozího: 16, Nově: 5

Celkem: 16 + 5 = 21

V 2022 zůstalo 9 (z grafu):

Odešlo: 21 − 9 = 12

Tvrzení říká více než 12 → 12 není větší než 12 → NE (nepravda)

✅ Výsledek

8.1) ANO 8.2) ANO 8.3) NE

⚠️ CERMAT chyták

Při úlohách s časovou řadou:

Sleduj vztah mezi roky: konec jednoho = začátek dalšího
Dopočítej chybějící údaje z bilance
Pozor na hranice: „více než 12" znamená > 12 (ne = 12)

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Čtení grafů a A/N tvrzení

Co si odnést z tohoto tématu

🧭 Strategie řešení

Přečti osy grafu — sleduj popisky, měřítko, jednotky
Dopočítej chybějící údaje z dalších podmínek v zadání
U každého tvrzení: vypočítej obě strany numericky a porovnej
Nezapomeň na přesné hranice: „více než" (>) vs „alespoň" (≥)

⚠️ Typické chytáky

„O třetinu více" (×4/3) ≠ „třikrát více" (×3) — jeden z nejčastějších chytáků!
Přesná hranice: „větší než 12" znamená > 12, NE = 12
Chybějící údaj v grafu — musíš ho dopočítat z jiné podmínky
U časových řad: konec jednoho roku = začátek dalšího

❌ Nejčastější chyby

Špatné čtení hodnot z grafu — pozor na měřítko osy
Záměna „o kolik více" a „kolikrát více"
Chybný základ při počítání zlomků (půlka z čeho?)
Přehlédnutí slova „alespoň", „více než", „právě"

📊 Čtení grafů a A/N tvrzení

🔑 Jak řešit A/N tvrzení

🎯 Rady pro CERMAT: Čtení grafů a A/N tvrzení