Obvody obrazců A a B se liší o 4 cm.
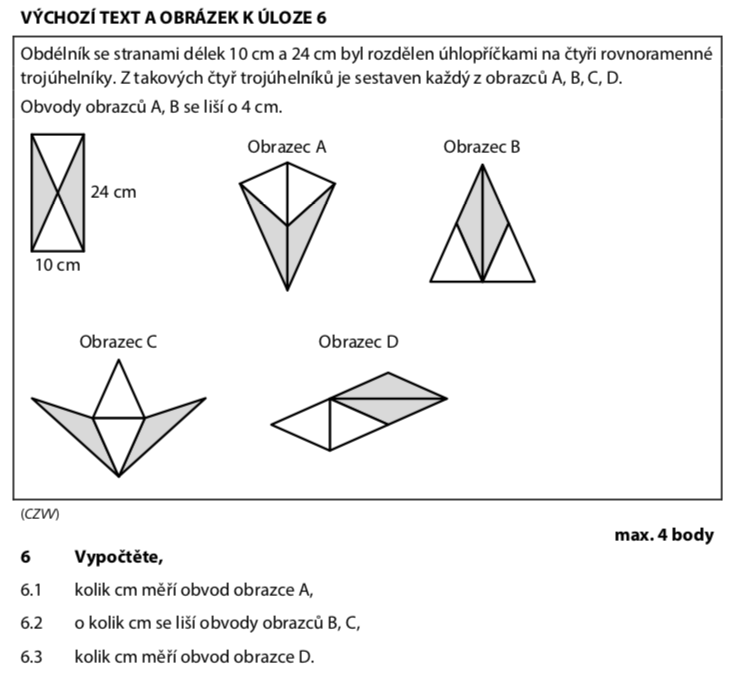
Obrazec A má tvar obdélníku složeného ze 4 trojúhelníků.
Jeho strany jsou strany původního obdélníku: 2 kratší strany 10 cm a 2 delší strany 24 cm.
Víme, že obvod B je o 4 cm větší než obvod A:
Obrazec B se skládá z 4 úhlopříček (každý trojúhelník přispěl jednou úhlopříčkou).
Ale také obsahuje 2 kratší strany obdélníku (2 · 10 = 20 cm).
Obrazec C obsahuje delší strany obdélníku (2 · 24 = 48 cm) a 4 úhlopříčky (4 · 13 = 52 cm).
Rozdíl mezi B a C:
Obrazec D je kosodélník složený ze 6 úhlopříček (každá má 13 cm, ale jde o poloviny, takže celkem 6 úseků po 13 cm).
U složitých obrazců:
- Najdi vztah mezi stranami — např. přes rozdíl obvodů
- Pozor na vnitřní hrany — ty se do obvodu nepočítají!
- Úhlopříčka obdélníku můžeš spočítat z rozměrů, ale tady stačilo použít rozdíl obvodů

Obvod čtverce se rovná obvodu trojúhelníku, ale je o 8 cm menší než obvod obdélníku.
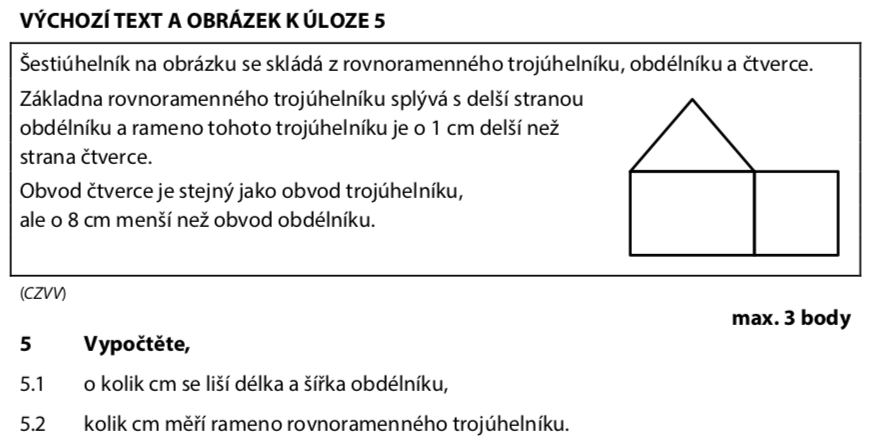
Obvod obdélníku je o 8 cm větší než obvod čtverce.
Obdélník: o = 2·(a + b). Čtverec: o = 4·a.
Rozdíl 8 cm pochází z toho, že obdélník má 2 delší strany místo 2 stran čtverce:
Obvod čtverce = obvod trojúhelníku.
Základna trojúhelníku = delší strana obdélníku = strana čtverce + 4 cm.
Rameno trojúhelníku = strana čtverce + 1 cm.
Protože obvody jsou stejné:
Strana čtverce je 6 cm.
Rameno trojúhelníku je o 1 cm delší než strana čtverce:
Při práci s obvody složených útvarů:
- Rozlož vztahy mezi stranami — co je delší, co kratší, o kolik
- Využij rozdílu obvodů k nalezení konkrétních délek
- Zkontroluj si výsledek dosazením zpět do podmínky

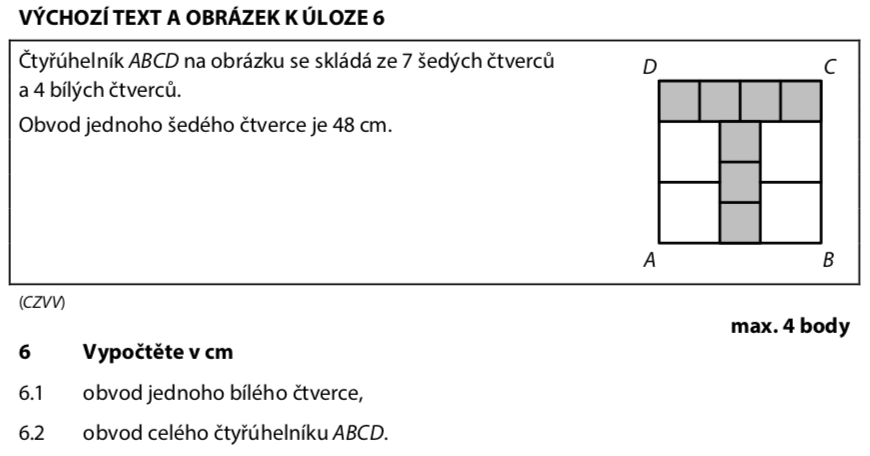
Obvod jednoho šedého čtverce je 48 cm.
Podle obrázku jsou 3 šedé čtverce nad sebou vedle jednoho bílého čtverce:
Tato výška je stejná jako 2 bílé čtverce (viz obrázek):
Celý čtyřúhelník ABCD má tvar čtverce!
Jeho strana odpovídá 4 šedým čtvercům pod sebou:
Při práci s obrazci složenými z čtverců:
- Hledej vztahy mezi stranami — např. 3 malé = 2 velké
- Pozor na vnitřní hrany — ty se do obvodu nepočítají!
- Zkontroluj si, jestli je celý útvar pravidelný (čtverec, obdélník)

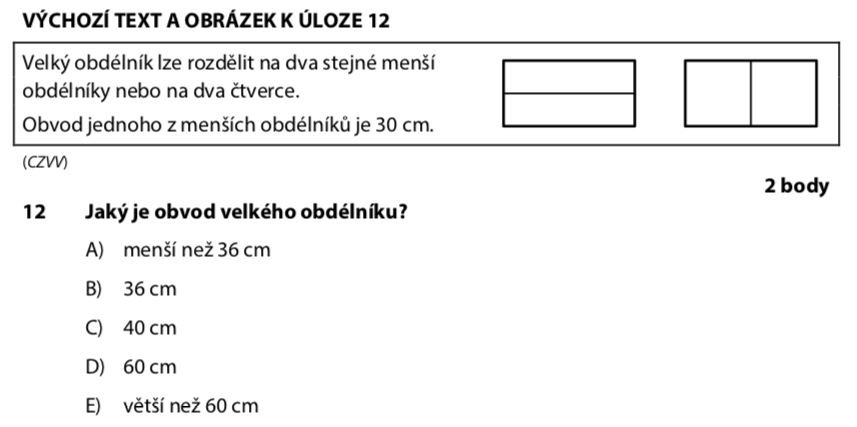
Velký obdélník lze rozdělit na 2 čtverce. To znamená, že jeho strany jsou v poměru 2:1.
Označme kratší stranu a, delší stranu 2a.
Menší obdélník vznikne rozdělením velkého obdélníku na polovinu.
Jeho strany jsou: a (šířka velkého) a a (polovina délky velkého)... ne, to by byl čtverec!
Správně: menší obdélník má strany a/2 a 2a (nebo a a a — to by byl čtverec).
Z obrázku vidíme, že menší obdélník má strany 1:4 (šířka celého : délka celého / 2).
Obvod menšího obdélníku = 30 cm.
Strany jsou v poměru 1:4 (kratší : delší).
Velký obdélník má strany 6 cm (2 × kratší strana menšího) a 12 cm (delší strana menšího).
Při řešení úloh s poměrem stran:
- Využij informaci o rozdělení na čtverce — to určuje poměr stran
- Z obvodu a poměru stran spočítej konkrétní délky
- Ověř si výsledek — strany velkého obdélníku musí být v poměru 2:1

🎯 Rady pro CERMAT: Obvody
Co si odnést z tohoto tématu
- Rozlož složený tvar na jednodušší útvary (čtverce, obdélníky, trojúhelníky)
- Hledej vztahy mezi stranami — co je delší, co kratší, o kolik
- Využij rozdílu obvodů k nalezení neznámých délek
- Pozor na vnitřní hrany — ty se do obvodu nepočítají!
- Záměna strany a úhlopříčky — úhlopříčka je delší než strana!
- Zapomenutí na vnitřní hrany — pouze vnější strany tvoří obvod
- U poměru stran (např. 1:2) — správně odvodit obě strany z obvodu
- Sčítání vnitřních hran do obvodu
- Nesprávné odvození neznámé strany z rozdílu obvodů
- Zapomenutí, že u čtverce všechny strany jsou stejné (o = 4·a)