← Zpět na rozcestník

⏪ Pracujeme pozpátku

Když znáš výsledek, pracuj od konce — otoč operace!

🔑 Práce pozpátku — obrať operace!

Procvičuj příklady z přijímaček:
📋 Zadání — 2. řádný termín, Úloha 13 (5 bodů)
V každém diagramu se stejné symboly nahradí stejným kladným celým číslem a do prázdného oválu se doplní takové celé číslo, aby byly všechny výpočty ve směru šipek správné.
13.1)
4 →(· ⊙ · ⊙)→ 100 →(: 4 − 2·⊙)→ ( )
13.2)
( ) →(: ✱ + ✱)→ 10 →(· ✱ − ✱)→ 72
13.3)
480 →(: ⊙ − 10)→ ( ) →(· 10 − ⊙)→ 120

Možnosti: A) 13, B) 14, C) 15, D) 16, E) 17, F) jiné číslo

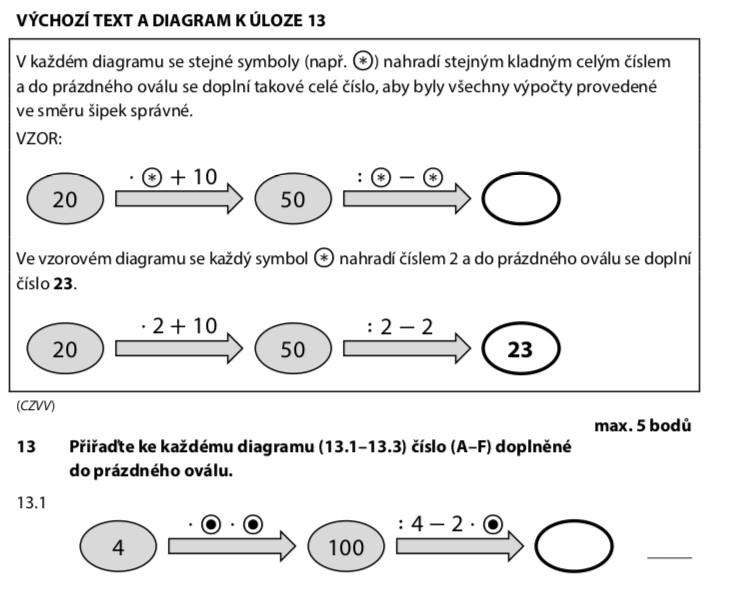
Zadání 13.1 Zadání 13.2-13.3
1 Diagram 13.1 — najdeme symbol ⊙

Z prvního kroku víme: 4 · ⊙ · ⊙ = 100

⊙ · ⊙ = 100 : 4 = 25

Jaké číslo krát samo sebe dá 25? To je 5! (protože 5 · 5 = 25)

⊙ = 5
2 Diagram 13.1 — dopočítáme prázdný ovál

Teď víme, že ⊙ = 5. Pokračujeme druhým krokem diagramu:

100 : 4 − 2 · 5 = 25 − 10 = 15

Odpověď pro 13.1: C) 15

3 Diagram 13.2 — pracujeme pozpátku od konce

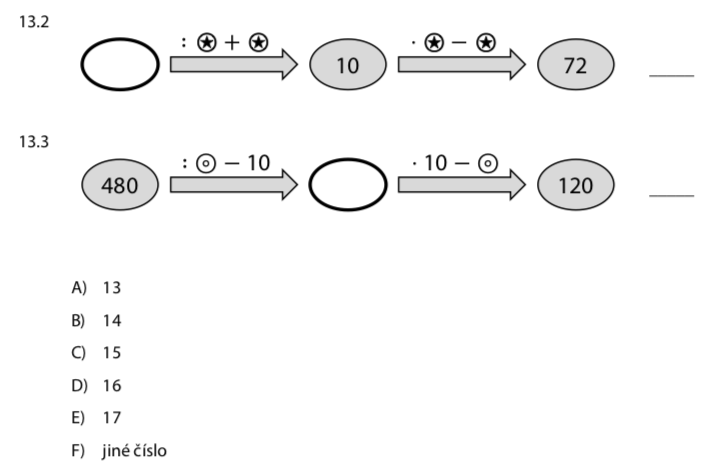
Začneme od konce a jdeme pozpátku! Od čísla 72 zpět k 10:

✱ · 10 − ✱ = 72

To je totéž jako: 9 · ✱ = 72 (devítinásobek ✱)

✱ = 72 : 9 = 8
4 Diagram 13.2 — číslo v prázdném oválu

Víme, že ✱ = 8. Teď dopočítáme číslo v prvním oválu:

číslo : 8 + 8 = 10
číslo : 8 = 10 − 8 = 2
číslo = 2 · 8 = 16

Odpověď pro 13.2: D) 16

5 Diagram 13.3 — zkoušíme hodnoty symbolu

Máme: 480 : ⊙ − 10 = číslo v oválu, pak: číslo · 10 − ⊙ = 120

Zkusíme různé dělitele čísla 480. Zkusme ⊙ = 20:

480 : 20 = 24
24 − 10 = 14 (číslo v oválu)

Ověříme druhý krok:

14 · 10 − 20 = 140 − 20 = 120 ✓

Odpověď pro 13.3: B) 14

✅ Výsledek
13.1 → C (15)    13.2 → D (16)    13.3 → B (14)
💡 Tip pro CERMAT

U diagramů začni tam, kde je nejvíc informací. Když znáš oba konce řetězce, pracuj od jednoho a ověř druhým.

Pozor: u 13.2 byl klíč v rozpoznání, že ✱ · 10 − ✱ je totéž jako 9 · ✱!

📝 Oficiální řešení CERMAT
Řešení Řešení
📋 Zadání — 1. náhradní termín, Úloha 10 (2 body)
Honza má kouzelný provázek. Pokaždé když jej rozstřihne, kratší kus zmizí a delší se prodlouží na dvojnásobek.

Provázek měřil 44 cm a Honza ho dvakrát rozstřihl. V obou případech zmizela stejně dlouhá část. Po prvním prodloužení měřil 66 cm.

Kolik cm měřil po druhém prodloužení?

Možnosti: A) 66 cm, B) 88 cm, C) 110 cm, D) 132 cm, E) jiný počet

Zadání
1 Pracujeme pozpátku od prvního střihu

Po prvním střihu: provázek měří 66 cm. Ale to je dvojnásobek delší části!

delší část = 66 : 2 = 33 cm

Klíčový trik — když jdeš pozpátku, „dvojnásobek" znamená že musíš dělit dvěma!

2 Kolik Honza ustřihl?

Původně provázek měřil 44 cm, po střihu zůstalo 33 cm.

ustřihl = 44 − 33 = 11 cm

Honza pokaždé ustřihne stejně dlouhý kus, takže i při druhém střihu ustřihne 11 cm!

3 Druhý střih

Začínáme se 66 cm. Honza ustřihne opět 11 cm:

66 − 11 = 55 cm (delší část)

Kouzelný provázek prodlouží delší část na dvojnásobek:

55 · 2 = 110 cm
✅ Výsledek
C) 110 cm
💡 Tip pro CERMAT

Klíčový trik — „dvojnásobek" znamená, že musíš DĚLIT dvěma, když jdeš pozpátku!

Když pracuješ pozpátku:

  • Místo násobení 2 → dělíš 2
  • Místo sčítání → odčítáš
  • Místo odčítání → sčítáš
📝 Oficiální řešení CERMAT
Řešení
📋 Zadání — 1. náhradní termín, Úloha 13 (5 bodů)
V každém diagramu se stejná písmena nahradí stejným číslem. Prázdné kroužky doplníme tak, aby výpočty ve směru šipek seděly.
13.1)

Kruhový diagram: ( ) →(+3)→ levý →(−K)→ 2 →(+K)→ pravý →(:K)→ ( )

13.2)

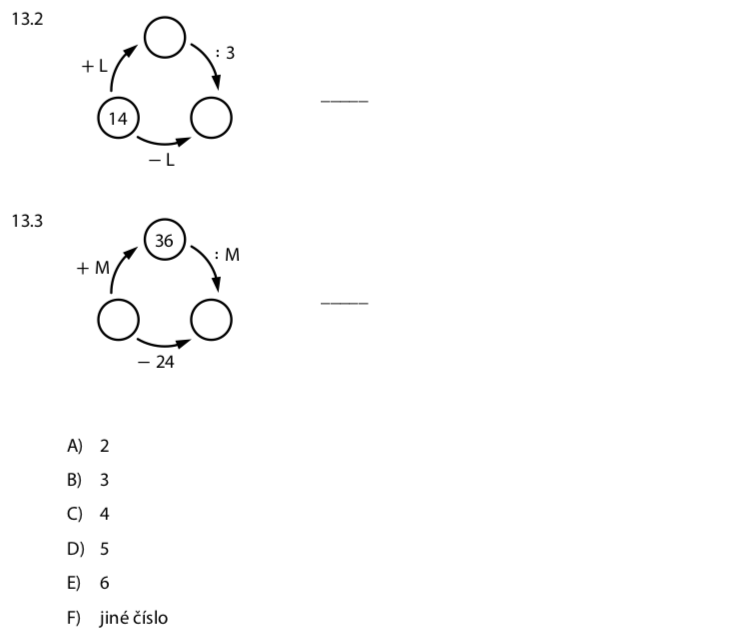
Kruhový diagram: ( ) →(+L)→ horní →(:3)→ pravý →(−L)→ 14 →(+L)→ ( )

13.3)

Kruhový diagram: ( ) →(+M)→ 36 →(:M)→ pravý →(−24)→ dolní →(+M)→ ( )

Možnosti: A) 2, B) 3, C) 4, D) 5, E) 6, F) jiné číslo

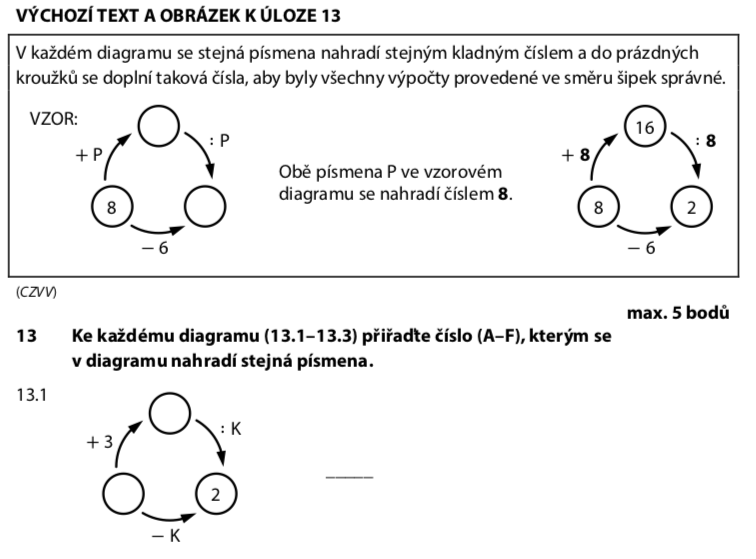
Zadání 13.1-13.2 Zadání 13.3
1 Diagram 13.1 — hledáme K

Obrátíme směr šipek od čísla 2 a pracujeme pozpátku:

2 + K + 3 = dvojnásobek K

To znamená: K + 5 = 2 · K

K = 5

Odpověď pro 13.1: D) 5

2 Diagram 13.2 — hledáme L

Obráceným směrem vytvoříme kruh. Číslo 14 zvýšené o L vydělíme 3. Po zvýšení opět o L se vrátíme zpět.

Ztráta vytvořená dělením je právě L. Platí, že dva pomyslné dílky přiřadíme ke 14 a L znamená jeden dílek.

14 = 2 · dílek → dílek = 7
L = 7

Odpověď pro 13.2: F) jiné číslo (7)

3 Diagram 13.3 — obrátíme pravou a dolní šipku

Obrátíme pravou šipku a začneme dole vpravo. Toto číslo vynásobené číslem M:

36 : M musí dát stejný výsledek jako 12 − M

Zkoušíme čísla, které dělí 36 beze zbytku a jsou menší než 12:

M = 2: 36:2 = 18, ale 12−2 = 10 ✗
M = 3: 36:3 = 12, ale 12−3 = 9 ✗
M = 4: 36:4 = 9, ale 12−4 = 8 ✗
M = 6: 36:6 = 6, a 12−6 = 6 ✓

Odpověď pro 13.3: E) 6

✅ Výsledek
13.1 → D (5)    13.2 → F (7)    13.3 → E (6)
💡 Tip pro CERMAT

U kruhových diagramů:

  • Obráť směr šipek od známého čísla a pracuj pozpátku
  • Když vidíš podmínku typu „po vydělení se vrátíme zpět", použij pomyslné dílky
  • U složitějších rovnic zkus zkoušet hodnoty — všechna čísla budou malá (typicky 1–10)
📝 Oficiální řešení CERMAT
Řešení Řešení

🎯 Rady pro CERMAT: Práce pozpátku

Co si odnést z tohoto tématu

🧭 Strategie řešení
  • Začni tam, kde máš nejvíc informací — obvykle od konce nebo od známého čísla
  • Obrať operace: sčítání ↔ odčítání, násobení ↔ dělení
  • U diagramů: obrať směr šipek a inverzní operace aplikuj v opačném pořadí
  • Když najdeš symbol/písmeno, ověř výsledek dosazením zpět do původního diagramu
⚠️ Typické chytáky
  • „Dvojnásobek" pozpátku znamená DĚLIT dvěma, ne násobit!
  • U kruhových diagramů pozor: musíš se vrátit zpět na začátek — to je klíčová podmínka
  • Když pracuješ se symboly (⊙, ✱, písmeny), pozor na to, že stejný symbol má všude stejnou hodnotu
  • U slovních úloh typu „kouzelný provázek": pozor na to, že stejná část mizí při každém střihu
❌ Nejčastější chyby
  • Zapomenout otočit operaci — místo násobení dělíš, místo sčítání odčítáš
  • U výrazů typu 10·✱ − ✱ nerozpoznat, že to je totéž jako 9·✱
  • Nezkoušet různé hodnoty systematicky — začni od 1 a postupuj výš
  • U diagramů: neověřit výsledek zpětným dosazením do všech kroků