Technika dílků | CERMAT 2023

📋 Zadání — 1. řádný termín, Úloha 2 (4 body)

2.1)

O kolik litrů se liší čtvrtina z 24 litrů a třetina z 12 litrů?

2.2)

Součin dvou čísel je roven 180. Jedno z nich zvětšíme dvakrát a druhé zmenšíme šestkrát. Jaký bude nový součin?

1 Příklad 2.1: Čtvrtina z 24 litrů

Čtvrtina znamená rozdělit celek na 4 dílky. Jaká je hodnota jednoho dílku?

24 : 4 = 6 litrů

Čtvrtina z 24 litrů = 6 litrů

2 Příklad 2.1: Třetina z 12 litrů

Třetina znamená rozdělit celek na 3 dílky. Spočítáme jeden dílek:

12 : 3 = 4 litry

Třetina z 12 litrů = 4 litry

3 Příklad 2.1: Rozdíl

Máme dvě hodnoty: 6 litrů a 4 litry. Jaký je mezi nimi rozdíl?

6 − 4 = 2 litry

Odpověď: Liší se o 2 litry.

4 Příklad 2.2: Co se děje se součinem?

Máme součin dvou čísel = 180. Teď jedno číslo zvětšíme 2× a druhé zmenšíme 6×.

Jak to ovlivní výsledek?

× 2 a : 6 → celkový efekt: × 2 : 6 = : 3

Součin se zmenší třikrát.

5 Příklad 2.2: Nový součin

Původní součin byl 180. Nový součin bude třikrát menší:

180 : 3 = 60

Odpověď: Nový součin = 60

✅ Výsledek

2.1) 2 litry 2.2) 60

💡 Tip pro CERMAT

Když se ptají na zlomek z nějaké hodnoty, vždy děl celkem počtem dílků:

Čtvrtina = 1/4 → dělíme 4
Třetina = 1/3 → dělíme 3
Polovina = 1/2 → dělíme 2

U součinu platí: zvětšení jednoho činitele a zmenšení druhého se vynásobí.

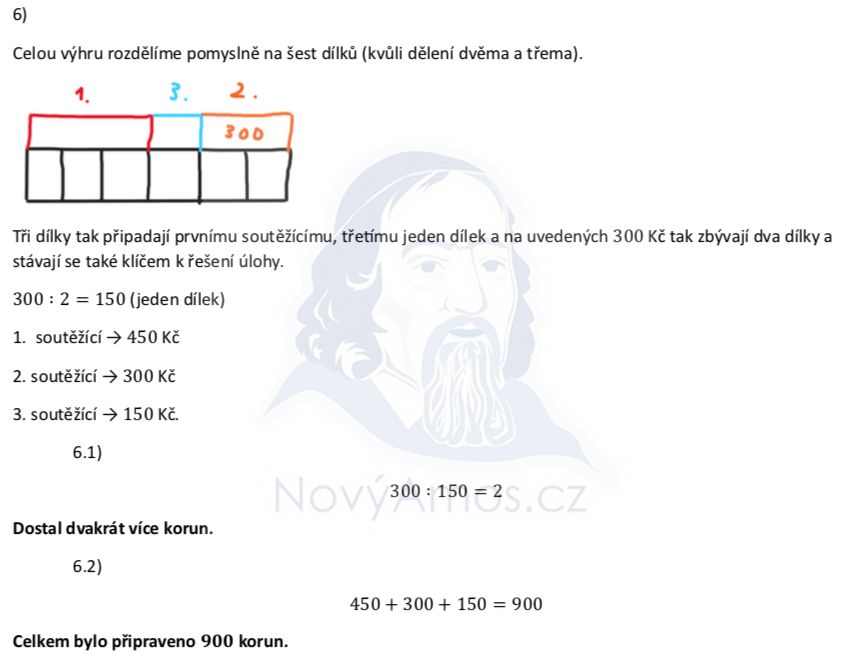
📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 6 (3 body)

Pro tři soutěžící je připravena částka na odměny. První soutěžící dostal polovinu celé částky, druhý soutěžící dostal 300 Kč a třetí soutěžící dostal třikrát méně než první soutěžící.

6.1)

Kolikrát více dostal druhý soutěžící než třetí?

6.2)

Jaká byla celková částka?

1 Rozdělíme celou částku na dílky

První dostal polovinu → 3 dílky. Třetí dostal třikrát méně než první → 1 dílek.

Dohromady tedy: 3 dílky (první) + 1 dílek (třetí) = 4 dílky.

Druhý dostal zbytek → zbývá ještě 2 dílky.

Celkem: 3 + 2 + 1 = 6 dílků

2 Hodnota jednoho dílku

Druhý soutěžící dostal 300 Kč a to odpovídá 2 dílkům.

1 dílek = 300 : 2 = 150 Kč

Teď můžeme dopočítat všechny odměny:

První: 3 dílky = 3 × 150 = 450 Kč
Druhý: 2 dílky = 2 × 150 = 300 Kč
Třetí: 1 dílek = 150 Kč

3 Otázka 6.1: Kolikrát více?

Druhý dostal 300 Kč, třetí dostal 150 Kč. Kolikrát více?

300 : 150 = 2×

Druhý dostal 2× více než třetí.

4 Otázka 6.2: Celková částka

Sečteme všechny odměny:

450 + 300 + 150 = 900 Kč

Nebo můžeme použít dílky: 6 dílků × 150 Kč = 900 Kč

✅ Výsledek

6.1) 2× více 6.2) 900 Kč

💡 Tip pro CERMAT

Když v úloze máš „třikrát méně", znamená to poměr 1:3 (ne rozdíl!). První má 3 dílky, třetí má 1 dílek.

Celkový počet dílků pak musí odpovídat celému celku (v tomto případě všem penězům).

📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 9 (2 body)

Maminka koupila tři zákusky. První zákusek stál 72 Kč. Druhý zákusek byl o čtvrtinu levnější než první. Třetí zákusek stál třetinu celkové ceny tří zákusků.

O kolik korun byl třetí zákusek dražší než druhý?

1 Cena druhého zákusku

Druhý zákusek byl o čtvrtinu levnější než první (72 Kč).

Čtvrtina z 72 Kč:

72 : 4 = 18 Kč

Druhý zákusek:

72 − 18 = 54 Kč

2 Cena prvních dvou zákusků

První a druhý zákusek dohromady:

72 + 54 = 126 Kč

Průměr prvních dvou:

126 : 2 = 63 Kč

3 Cena třetího zákusku

Třetí zákusek stál třetinu celkové ceny. To znamená, že zbývající dva zákusky (první a druhý) stály dvě třetiny.

Pokud 2/3 = 126 Kč, pak:

1/3 = 126 : 2 = 63 Kč

Třetí zákusek = 63 Kč

4 Rozdíl mezi třetím a druhým

Třetí stál 63 Kč, druhý stál 54 Kč:

63 − 54 = 9 Kč

Třetí zákusek byl o 9 Kč dražší než druhý.

9 Kč je méně než 12 Kč → správná odpověď je A)

✅ Výsledek

A) o méně než 12 korun (o 9 Kč)

⚠️ CERMAT chyták

Pozor na formulaci „o čtvrtinu levnější" — neznamená to „čtvrtina z původní ceny", ale „původní cena minus čtvrtina"!

A když víš, že třetí zákusek = 1/3 celku, pak první a druhý = 2/3 celku. Z toho se dá dopočítat třetí zákusek.

📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 10 (2 body)

Máme 78 mincí: pětikorunové a desetikorunové. Celková hodnota pětikorunových mincí se rovná celkové hodnotě desetikorunových mincí.

Jaká je celková hodnota všech mincí?

1 Jaký je poměr mincí?

Hodnota pětikorun = hodnota desetikorun.

Aby měly stejnou hodnotu, musí být pětikorun 2× více než desetikorun!

2 × (počet desetikorun) = počet pětikorun

Poměr: 2:1 (pětikoruny : desetikoruny)

2 Rozdělíme mince na dílky

Celkem máme 78 mincí a poměr je 2:1 → celkem 3 dílky.

1 dílek = 78 : 3 = 26 mincí

Pětikoruny = 2 dílky = 2 × 26 = 52 mincí

Desetikoruny = 1 dílek = 26 mincí

3 Hodnota pětikorunových mincí

52 × 5 Kč = 260 Kč

4 Hodnota desetikorunových mincí

26 × 10 Kč = 260 Kč

Výborně! Hodnoty se opravdu rovnají. ✅

5 Celková hodnota

260 + 260 = 520 Kč

Odpověď: B) 520 korun

✅ Výsledek

B) 520 korun

💡 Tip pro CERMAT

Když hodnoty dvou skupin mají být stejné, ale jednotky jsou jiné (5 Kč vs. 10 Kč), musí být skupin různě!

Menší hodnota → více kusů. Větší hodnota → méně kusů. Poměr je opačný k poměru hodnot.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 4 (4 body)

4.1)

Zapůjčení županu je o 30 Kč dražší než zapůjčení osušky. Cena za pět osušek je stejná jako cena za tři župany. Kolik korun stojí zapůjčení županu?

4.2)

Jirka, Míša a Pavla plavali v bazénu. Celkem uplovali šedesát bazénů. Jirka uplaval stejný počet bazénů jako Míša a Míša uplavala dvakrát více bazénů než Pavla. Kolik bazénů uplavala Míša?

1 Příklad 4.1: Vztah mezi županem a osuškou

Župan je o 30 Kč dražší než osuška. Zapišme to:

1 župan = 1 osuška + 30 Kč

Zároveň víme: 5 osušek = 3 župany

2 Příklad 4.1: Vyjádříme župany pomocí osušek

Každý župan je „osuška + 30". Tři župany jsou:

3 župany = 3 osušky + 3 × 30 = 3 osušky + 90 Kč

Ale víme, že 5 osušek = 3 župany, tedy:

5 osušek = 3 osušky + 90 Kč

2 osušky = 90 Kč

1 osuška = 45 Kč

3 Příklad 4.1: Cena županu

Župan je o 30 Kč dražší než osuška:

župan = 45 + 30 = 75 Kč

4 Příklad 4.2: Rozdělíme bazény na dílky

Pavla = 1 dílek, Míša = 2 dílky (dvakrát více než Pavla), Jirka = 2 dílky (stejně jako Míša)

Celkem: 1 + 2 + 2 = 5 dílků

60 bazénů = 5 dílků

1 dílek = 60 : 5 = 12 bazénů

5 Příklad 4.2: Kolik uplavala Míša?

Míša = 2 dílky:

2 × 12 = 24 bazénů

✅ Výsledek

4.1) 75 Kč 4.2) 24 bazénů

💡 Tip pro CERMAT

U složitějších slovních úloh:

Zapiš si vztahy, které znáš (např. „župan = osuška + 30")
Použij techniku dílků — každého rozdělíme na stejné části
Když víš, že „Míša = 2× Pavla", znamená to poměr 2:1

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 10 (2 body)

Sára, Lukáš, Dan a Adéla soutěžili. Počet bodů, které získala Sára, se rovnal počtu bodů, které získal Lukáš. Dan získal 60 bodů, což je o polovinu více bodů, než získali Sára s Lukášem dohromady, ale o čtvrtinu méně bodů než získala Adéla.

Který graf znázorňuje počty bodů jednotlivých soutěžících?

1 „O polovinu více" — co to znamená?

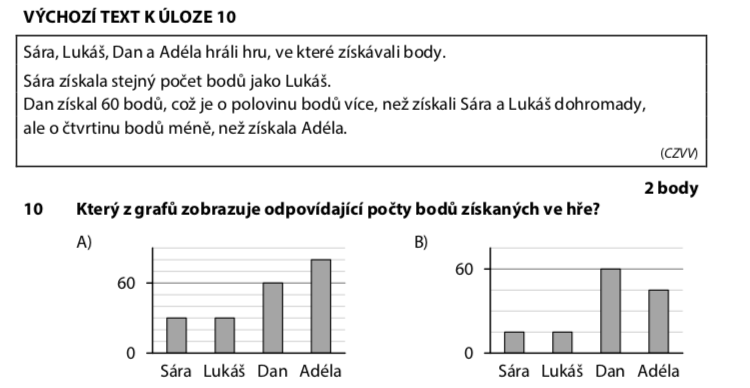
Dan získal 60 bodů = „o polovinu více" než Sára + Lukáš dohromady.

„O polovinu více" znamená: původní hodnota + polovina = 1,5× původní hodnoty.

Dan = 3/2 × (Sára + Lukáš)

60 = 3/2 × (Sára + Lukáš)

2 Dopočítáme Sáru + Lukáše

Když 60 = 3/2 × (Sára + Lukáš), pak:

Sára + Lukáš = 60 : 3/2 = 60 × 2/3 = 40 bodů

Sára = Lukáš, tedy každý má:

40 : 2 = 20 bodů

3 „O čtvrtinu méně" — co to znamená?

Dan má 60 bodů = „o čtvrtinu méně" než Adéla.

„O čtvrtinu méně" znamená: původní hodnota minus čtvrtina = 3/4 původní hodnoty.

Dan = 3/4 × Adéla

60 = 3/4 × Adéla

4 Dopočítáme Adélu

Adéla = 60 : 3/4 = 60 × 4/3 = 80 bodů

Máme všechny hodnoty:

Sára = 20 bodů
Lukáš = 20 bodů
Dan = 60 bodů
Adéla = 80 bodů

5 Který graf odpovídá?

Hledáme graf, kde: S ≈ 20, L ≈ 20, Dan ≈ 60, Adéla ≈ 80.

To odpovídá grafu D)

✅ Výsledek

D)

⚠️ CERMAT chyták

Pozor na formulace:

„O polovinu více" = 1,5× (ne 2×!)
„O čtvrtinu méně" = 3/4 (ne 1/4!)
„Třikrát více" = 3× (ne 4×!)

Slovo „O" znamená rozdíl (přidáváme nebo ubíráme). Bez slova „O" jde o násobek.

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 4 (4 body)

4.1)

Závodník uběhl trasu za tři hodiny. V první hodině uběhl třetinu celé trasy. V poslední hodině uběhl devět kilometrů, což byla čtvrtina celé trasy. Kolik kilometrů uběhl ve druhé hodině?

4.2)

Ema uběhla o devět set metrů kratší trasu než Marek. Třetina trasy, kterou uběhla Ema, se rovná pětině trasy, kterou uběhl Marek. Kolik metrů uběhl Marek?

1 Příklad 4.1: Celková délka trasy

Poslední hodina = 9 km = čtvrtina trasy.

1/4 trasy = 9 km

celá trasa = 4 × 9 = 36 km

2 Příklad 4.1: První hodina

V první hodině uběhl třetinu trasy:

1/3 × 36 = 12 km

3 Příklad 4.1: Druhá hodina

Zbývá vypočítat druhou hodinu. Víme celkovou trasu a první i třetí hodinu:

2. hodina = 36 − 12 − 9 = 15 km

4 Příklad 4.2: Poměr tras

1/3 Emy = 1/5 Marka. To znamená poměr 3:5 (Ema : Marek).

Rozdíl = 2 dílky = 900 m

1 dílek = 900 : 2 = 450 m

5 Příklad 4.2: Trasa Marka

Marek = 5 dílků:

5 × 450 = 2250 m

✅ Výsledek

4.1) 15 km 4.2) 2250 m

💡 Tip pro CERMAT

Když víš zlomek z celku (např. čtvrtina = 9 km), můžeš dopočítat celou hodnotu (9 × 4 = 36 km).

Když platí 1/3 Emy = 1/5 Marka, znamená to poměr 3:5. Vždy si rozkresli dílky!

📝 Oficiální řešení CERMAT

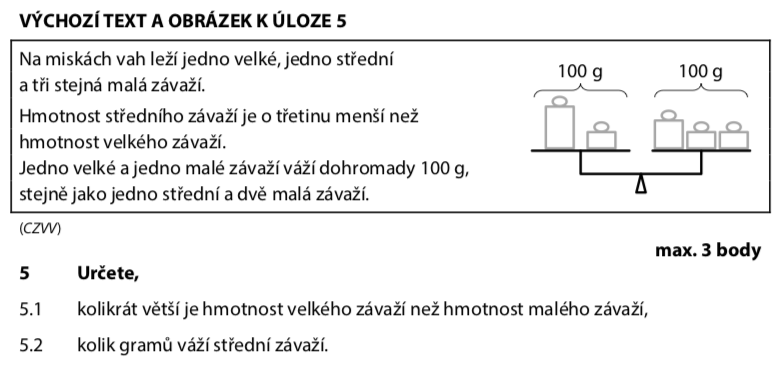
📋 Zadání — 2. náhradní termín, Úloha 5 (3 body)

Máme tři závaží. Hmotnost středního závaží je o třetinu menší než hmotnost velkého závaží. Součet hmotnosti velkého závaží a hmotnosti malého závaží je 100 gramů, což je rovno součtu hmotnosti středního závaží a dvojnásobku hmotnosti malého závaží.

5.1)

Kolikrát je větší hmotnost velkého závaží než hmotnost malého závaží?

5.2)

Kolik gramů má střední závaží?

1 Vztah velkého a středního závaží

Střední je o třetinu menší než velké. To znamená:

střední = 2/3 × velké

Pokud velké = 3 dílky, pak střední = 2 dílky.

2 Rovnice ze zadání

Velké + malé = 100 g = střední + 2× malé

Upravíme:

velké + malé = střední + malé + malé

velké = střední + malé

Když velké = 3 dílky a střední = 2 dílky, pak:

3 dílky = 2 dílky + malé

malé = 1 dílek

3 Otázka 5.1: Kolikrát větší?

Velké = 3 dílky, malé = 1 dílek:

3 : 1 = 3×

Velké závaží je 3× větší než malé.

4 Hodnota jednoho dílku

Velké + malé = 100 g, což je 3 dílky + 1 dílek = 4 dílky:

4 dílky = 100 g

1 dílek = 100 : 4 = 25 g

5 Otázka 5.2: Hmotnost středního

Střední = 2 dílky:

2 × 25 = 50 g

✅ Výsledek

5.1) 3× větší 5.2) 50 g

💡 Tip pro CERMAT

Složité slovní úlohy si rozpiš na vztahy:

„O třetinu menší" = 2/3 původní hodnoty
Když A + B = C + 2B, můžeš zjednodušit: A = C + B
Pracuj s dílky — všechny hodnoty vyjádři pomocí stejných dílků

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 10 (2 body)

Výška Anežky je o pětinu nižší než moje výška. Výška mého tatínka je o pětinu vyšší než moje výška. Anežka je o 60 centimetrů nižší než tatínek.

Kolik centimetrů měří Anežka?

1 Vyjádříme výšky pomocí dílků

Moje výška = 5 dílků (základ)

Anežka je o pětinu nižší → 4 dílky

Tatínek je o pětinu vyšší → 6 dílků

2 Rozdíl mezi tatínkem a Anežkou

Tatínek = 6 dílků, Anežka = 4 dílky

Rozdíl = 6 − 4 = 2 dílky

Tento rozdíl = 60 cm:

2 dílky = 60 cm

1 dílek = 60 : 2 = 30 cm

3 Výška Anežky

Anežka = 4 dílky:

4 × 30 = 120 cm

Odpověď: C) 120 cm

✅ Výsledek

C) 120 cm

💡 Tip pro CERMAT

Když máš vztahy „o X-tinu vyšší/nižší", vždy si zakresli dílky:

„O pětinu nižší" = 4/5 → z 5 dílků udělej 4
„O pětinu vyšší" = 6/5 → z 5 dílků udělej 6

Pak najdi rozdíl mezi dvěma hodnotami a dopočítej dílek!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 11 (2 body)

Na parkovišti je celkem 105 parkovacích míst obsazených autobusy nebo auty. Jeden autobus obsadí čtyři parkovací místa. Počet aut je třikrát větší než počet autobusů.

O kolik je počet aut větší než počet autobusů?

1 Kolik míst zabírá jedna skupina?

Počet aut = 3× počet autobusů

Představme si jednu „skupinu": 3 auta + 1 autobus

Autobus zabírá 4 místa, auto zabírá 1 místo:

1 skupina = 3 × 1 + 1 × 4 = 7 míst

2 Kolik skupin máme?

Celkem 105 parkovacích míst:

105 : 7 = 15 skupin

3 Počet autobusů a aut

15 skupin → každá má 1 autobus a 3 auta:

Autobusy = 15 × 1 = 15

Auta = 15 × 3 = 45

4 O kolik více?

45 − 15 = 30

Odpověď: B) o 30

✅ Výsledek

B) o 30

⚠️ CERMAT chyták

Pozor! Autobus zabírá 4 místa, ne 1!

Nejčastější chyba: zapomenout, že autobus zabírá více míst, a spočítat to, jako by každý zabíral jedno místo.

Správný postup: Vytvoř „skupinu" (3 auta + 1 autobus) a spočítej, kolik míst tato skupina zabere (3 + 4 = 7).

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Technika dílků

Co si odnést z tohoto tématu

🧭 Strategie řešení

Rozděl celek na dílky podle poměru (např. 3:1 → celkem 4 dílky)
Najdi hodnotu jednoho dílku (dělením celku počtem dílků)
Dopočítej ostatní hodnoty pomocí dílků
„O X-tinu více/méně" → přidej/uber dílky od celku (ne násobení!)

⚠️ Typické chytáky

„O třetinu méně" = 2/3 (ne 1/3!)
„Třikrát méně" = 1/3 (ne 2/3!)
Zlomek se vždy počítá z CELKU (ne z části)
Autobus zabírá 4 místa, ne 1 (nezapomeň na to!)

❌ Nejčastější chyby

Záměna „o třetinu" (rozdíl) a „třikrát" (poměr)
Nesprávný základ pro výpočet zlomku (část místo celku)
Zapomenutí, že některé věci zabírají více míst (autobus = 4 místa)
Zaměnění „o polovinu více" (= 1,5×) s „dvakrát více" (= 2×)

🧩 Technika dílků

🔑 Technika dílků

🎯 Rady pro CERMAT: Technika dílků