Pořadí operací a závorky

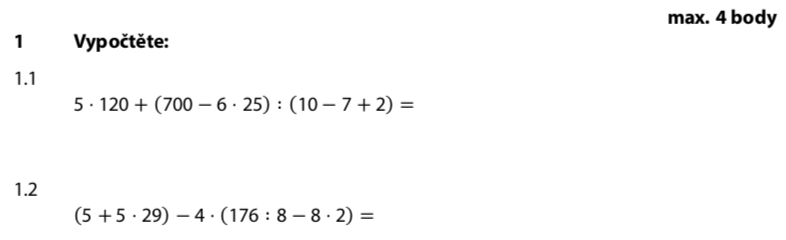
📋 Zadání — 1. řádný termín, Úloha 1 (4 body)

Vypočtěte:

1.1)

5 · 120 + (700 − 6 · 25) : (10 − 7 + 2) = ?

1.2)

(5 + 5 · 29) − 4 · (176 : 8 − 8 · 2) = ?

1 Příklad 1.1 — najdeme závorky

V příkladu jsou dvě závorky. Spočítáme je postupně. V první závorce je násobení i odčítání — násobení má přednost:

700 − 6 · 25 = 700 − 150 = 550

Druhá závorka je jednoduchá — jen sčítání a odčítání zleva doprava:

10 − 7 + 2 = 5

2 Příklad 1.1 — dopočítáme

Teď máme příklad bez závorek:

5 · 120 + 550 : 5

Násobení a dělení mají přednost:

5 · 120 + 550 : 5 = 600 + 110 = 710

3 Příklad 1.2 — závorky

První závorka: násobení má přednost před sčítáním!

5 + 5 · 29 = 5 + 145 = 150

Druhá závorka: dělení a násobení mají stejnou přednost, počítáme zleva doprava:

176 : 8 − 8 · 2 = 22 − 16 = 6

4 Příklad 1.2 — dopočítáme

Znovu: násobení má přednost před odčítáním!

150 − 4 · 6 = 150 − 24 = 126

✅ Výsledek

1.1) = 710 1.2) = 126

💡 Tip pro CERMAT

Vždy nejdřív spočítej závorky. Uvnitř závorek platí stejná pravidla — násobení a dělení mají přednost před sčítáním a odčítáním!

Pozor: i když vyřešíš závorku, nezapomeň, že násobení a dělení POŘÁD mají přednost před + a −.

📝 Oficiální řešení CERMAT

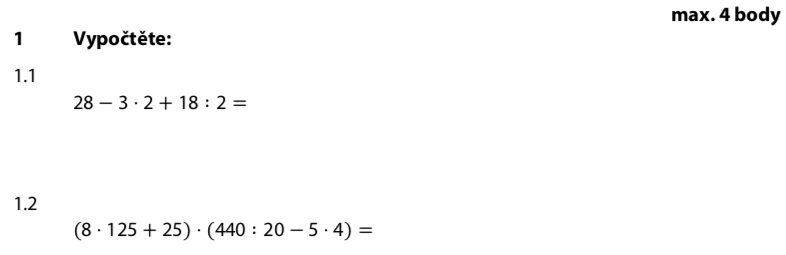
📋 Zadání — 2. řádný termín, Úloha 1 (4 body)

Vypočtěte:

1.1)

28 − 3 · 2 + 18 : 2 = ?

1.2)

(8 · 125 + 25) · (440 : 20 − 5 · 4) = ?

1 Příklad 1.1 — žádné závorky

V příkladu nejsou závorky, takže najdeme násobení a dělení a spočítáme je první:

28 − 3 · 2 + 18 : 2

28 − 6 + 9

Teď už jen sčítáme a odčítáme zleva doprava:

28 − 6 + 9 = 22 + 9 = 31

2 Příklad 1.2 — dvě závorky

První závorka: násobení má přednost!

8 · 125 + 25 = 1000 + 25 = 1025

Druhá závorka: dělení i násobení, počítáme zleva doprava:

440 : 20 − 5 · 4 = 22 − 20 = 2

3 Příklad 1.2 — vynásobíme

Násobíme výsledky závorek:

1025 · 2 = 2050

Pozor na chyták: Kdyby druhá závorka vyšla 0, celý příklad by byl = 0! (Cokoliv × 0 = 0.)

✅ Výsledek

1.1) = 31 1.2) = 2 050

💡 Tip pro CERMAT

Když v příkladu nejsou závorky (jako 1.1), nezapomeň na přednost · a : před + a −. Spočítej násobení a dělení VŠECHNA najednou, pak teprve sčítej a odčítej zleva doprava.

Typická chyba: 28 − 3 · 2 + 18 : 2 = 25 · 2 + 18 : 2 — to je ŠPATNĚ! Musíš spočítat násobení a dělení PRVNÍ, ne postupovat zleva doprava.

📝 Oficiální řešení CERMAT

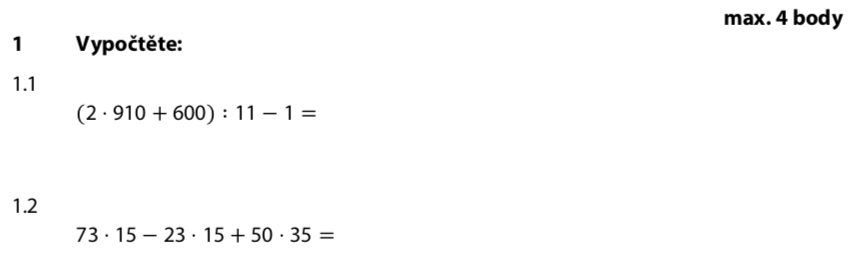
📋 Zadání — 1. náhradní termín, Úloha 1 (4 body)

Vypočtěte:

1.1)

(2 · 910 + 600) : 11 − 1 = ?

1.2)

73 · 15 − 23 · 15 + 50 · 35 = ?

1 Příklad 1.1 — závorka

V závorce je násobení i sčítání — násobení má přednost:

2 · 910 + 600 = 1820 + 600 = 2420

2 Příklad 1.1 — dopočítáme

Teď máme příklad: 2420 : 11 − 1

Pozor! Dělení má přednost před odčítáním:

2420 : 11 − 1 = 220 − 1 = 219

3 Příklad 1.2 — trik: vytýkání!

Všimni si: 73·15 − 23·15. Obě části mají společný činitel 15!

Můžeme to přepsat:

73·15 − 23·15 = (73 − 23)·15 = 50·15 = 750

A ještě: 50·35 = 1750, takže:

750 + 1750 = 2500

4 Bonus — ještě lepší trik!

Mohli jsme vytknout ještě jednou! Po prvním vytýkání máme:

50·15 + 50·35

Obě mají společný činitel 50:

50·15 + 50·35 = 50·(15+35) = 50·50 = 2500

Ušetřili jsme spoustu násobení!

✅ Výsledek

1.1) = 219 1.2) = 2 500

⚠️ CERMAT chyták

Vytýkání společného činitele — CERMAT tohle miluje! Když vidíš stejné číslo v násobení (73·15 − 23·15), můžeš ho „vytknout": (73−23)·15. Ušetříš čas a vyhneš se chybám ve výpočtu!

Pravidlo: a·b + a·c = a·(b+c) nebo a·b − a·c = a·(b−c)

📝 Oficiální řešení CERMAT

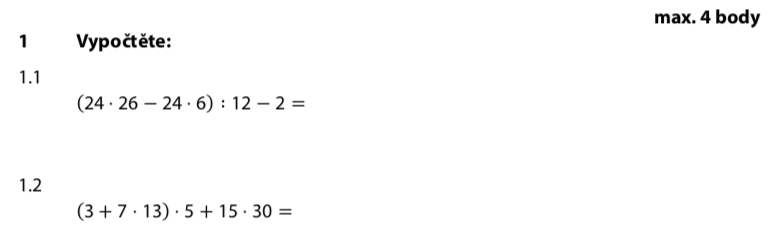
📋 Zadání — 2. náhradní termín, Úloha 1 (4 body)

Vypočtěte:

1.1)

(24 · 26 − 24 · 6) : 12 − 2 = ?

1.2)

(3 + 7 · 13) · 5 + 15 · 30 = ?

1 Příklad 1.1 — vytýkání v závorce

V závorce: 24·26 − 24·6. Oba mají činitel 24!

Vytkneme:

24·26 − 24·6 = 24·(26−6) = 24·20 = 480

2 Příklad 1.1 — dopočítáme

Teď máme: 480 : 12 − 2

Dělení má přednost před odčítáním!

480 : 12 − 2 = 40 − 2 = 38

3 Příklad 1.2 — závorka

V závorce: násobení má přednost před sčítáním!

3 + 7 · 13 = 3 + 91 = 94

4 Příklad 1.2 — dopočítáme

Teď máme: 94·5 + 15·30

Oba násobení, pak sčítání:

94·5 + 15·30 = 470 + 450 = 920

✅ Výsledek

1.1) = 38 1.2) = 920

💡 Tip pro CERMAT

Vytýkání se na přijímačkách 2023 objevilo hned dvakrát! (1. i 2. náhradní termín.) Vždy hledej společný činitel — výpočet bude mnohem jednodušší.

Bez vytýkání: 24·26 − 24·6 = 624 − 144 = 480 (složité!)
S vytýkáním: 24·(26−6) = 24·20 = 480 (jednoduché!)

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Pořadí operací

Co si odnést z tohoto tématu

🧭 Strategie řešení

Závorky počítej vždy jako první — i když v nich je další násobení nebo dělení
Po vyřešení závorky se vrať k pravidlům (· a : mají přednost před + a −)
Hledej společné činitele — vytýkání ti ušetří čas a vyhneš se chybám
Bez závorek: spočítej VŠECHNA · a : zleva doprava, pak teprve + a −

⚠️ Typické chytáky

Vytýkání společného činitele (73·15 − 23·15 = 50·15) — CERMAT to v roce 2023 použil hned 2×!
Závorka, která vyjde 0 — pak je celý součin roven 0 (cokoliv × 0 = 0)
Po vyřešení závorky: dělení má stále přednost před + a − (např. 2420 : 11 − 1 ≠ 2420 : 10)

❌ Nejčastější chyby

Zapomenout na přednost · a : po vyřešení závorky (např. 2420 : 11 − 1 — dělení má pořád přednost!)
Počítat zleva doprava bez ohledu na · a : (u příkladů bez závorek)
Nepodívat se, jestli jde něco zkrátit nebo vytknout (ušetříš spoustu práce!)

🔢 Pořadí operací a závorky

🔑 Zlaté pravidlo pořadí operací

🎯 Rady pro CERMAT: Pořadí operací