Poměry a skupiny | CERMAT 2022

📋 Zadání — 1. řádný termín, Úloha 10 (2 body)

Děti se rozdělily do 4členných hlídek. V každé hlídce byla právě 1 dívka. Celkem bylo 36 chlapců. Kolik bylo celkem dětí?

A) 48 B) 45 C) 42 D) 40 E) jiný výsledek

1 Kolik chlapců je v jedné hlídce?

Každá hlídka má 4 děti a z toho 1 dívku.

Takže v jedné hlídce je chlapců:

4 − 1 = 3 chlapci

2 Kolik je hlídek?

Celkem je 36 chlapců a v každé hlídce jsou 3 chlapci:

36 : 3 = 12 hlídek

3 Kolik dětí celkem?

V každé hlídce je 1 dívka → celkem dívek: 12

36 chlapců + 12 dívek = 48 dětí

Nebo: 12 hlídek × 4 děti = 48

✅ Výsledek

A) 48 dětí

💡 Tip pro CERMAT

Najdi skupinu (hlídku), spočítej, kolik je v ní chlapců, a odtud urči počet skupin. Klasická CERMAT technika: z jedné části skupiny dopočítáš celek!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. řádný termín, Úloha 12 (2 body)

Stejný počet dívek i chlapců cvičil. Dívky cvičily v 9členných skupinách, chlapci v 6členných. Dívky měly o 30 skupin méně než chlapci. Kolik bylo celkem skupin?

A) méně než 70 B) 70 C) 90 D) 150 E) více než 150

1 Co víme?

Dívek a chlapců je stejně — řekněme n.

Dívky cvičí po 9, chlapci po 6.

Počet n musí jít vydělit 9 i 6 beze zbytku (celé skupiny).

Nejmenší společný násobek (NSN) čísel 6 a 9 je 18.

2 Zkusíme to s dílky po 18

Když vezmeme 18 dětí (dívek nebo chlapců):

Skupin dívek: 18 : 9 = 2

Skupin chlapců: 18 : 6 = 3

Rozdíl: 3 − 2 = 1 skupina navíc na každých 18 dětí.

Na každých 18 dětí mají chlapci o 1 skupinu více

3 Kolik dětí celkem?

Rozdíl je 30 skupin. Na každých 18 dětí je rozdíl 1 skupina.

30 × 18 = 540 dětí (dívek i chlapců)

4 Kolik skupin celkem?

Skupin dívek: 540 : 9 = 60

Skupin chlapců: 540 : 6 = 90

Kontrola: 90 − 60 = 30 ✓

60 + 90 = 150 skupin

✅ Výsledek

D) 150 skupin

💡 Tip pro CERMAT

Tohle je klasická „Cermatovina"! Když je stejný počet dětí rozdělený do různě velkých skupin, najdi nejmenší společný násobek a pracuj s ním jako s dílkem. Rozdíl skupin ti pak řekne, kolik dílků je celkem.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 9 (2 body)

Květinářka měla 105 růží — červených a bílých. Uvázala z nich kytice po 5 růžích, v každé kytici byly právě 3 červené růže. Kolik bylo bílých růží?

A) 21 B) 35 C) 42 D) 63 E) více než 63

1 Kolik kytic?

Celkem 105 růží, v každé kytici 5 růží:

105 : 5 = 21 kytic

2 Kolik červených a kolik bílých?

V každé kytici jsou právě 3 červené → zbytek jsou bílé: 5 − 3 = 2 bílé

Červených celkem: 21 × 3 = 63

Bílých celkem:

21 × 2 = 42 bílých růží

Kontrola: 63 + 42 = 105 ✓

✅ Výsledek

C) 42 bílých růží

💡 Tip pro CERMAT

Všimni si slovíčka „právě 3" — to znamená přesně 3, ne „alespoň 3". CERMAT tím říká, že v každé kytici jsou vždy stejně červené a bílé růže. Stačí najít počet kytic a vynásobit!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 3 (4 body)

Kapli prohlédlo 630 návštěvníků. 5 průvodců, každý provedl 4 skupiny dopoledne a 2 skupiny odpoledne. Všechny skupiny byly stejně početné.

3.1) Kolik návštěvníků bylo v jedné skupině?

3.2) Kolik návštěvníků přišlo dopoledne?

1 Kolik skupin celkem?

Každý průvodce provedl: 4 dopoledne + 2 odpoledne = 6 skupin

Průvodců je 5:

5 × 6 = 30 skupin celkem

2 3.1) Kolik návštěvníků v jedné skupině?

Celkem 630 návštěvníků ve 30 skupinách (všechny stejně velké):

630 : 30 = 21 návštěvníků

3 3.2) Kolik návštěvníků dopoledne?

Dopoledne: každý průvodce provedl 4 skupiny.

Dopoledních skupin celkem: 5 × 4 = 20

20 × 21 = 420 návštěvníků

✅ Výsledek

3.1) 21 návštěvníků 3.2) 420 návštěvníků

💡 Tip pro CERMAT

Postupuj od celku k částem: nejdřív celkový počet skupin, pak velikost jedné skupiny, a nakonec dopoledne vs. odpoledne. Nezapomeň, že průvodců je 5 — to se snadno přehlédne!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 4 (4 body)

300 kříd je v menších a větších krabičkách. Menších krabiček je 5 a celkem v nich je tolik kříd jako ve 3 větších krabičkách. Větší krabička obsahuje 10 kříd.

4.1) Kolik kříd je v jedné malé krabičce?

4.2) Kolik je větších krabiček?

1 4.1) Kolik kříd v malé krabičce?

Ve 3 větších krabičkách je:

3 × 10 = 30 kříd

A to je stejně jako v 5 menších krabičkách. Takže:

30 : 5 = 6 kříd v malé krabičce

2 4.2) Kolik kříd je v malých krabičkách?

5 malých krabiček × 6 kříd:

5 × 6 = 30 kříd v malých krabičkách

Na větší krabičky zbývá: 300 − 30 = 270 kříd

3 4.2) Kolik větších krabiček?

Větší krabička má 10 kříd, zbývá 270 kříd:

270 : 10 = 27 větších krabiček

Kontrola: 5 × 6 + 27 × 10 = 30 + 270 = 300 ✓

✅ Výsledek

4.1) 6 kříd 4.2) 27 větších krabiček

💡 Tip pro CERMAT

Klíčová informace je „v 5 menších je tolik jako ve 3 větších". Začni tím, co znáš (větší krabička = 10 kříd), a dopočítej malou. Pak odečti od celku a doděláš druhou část.

📝 Oficiální řešení CERMAT

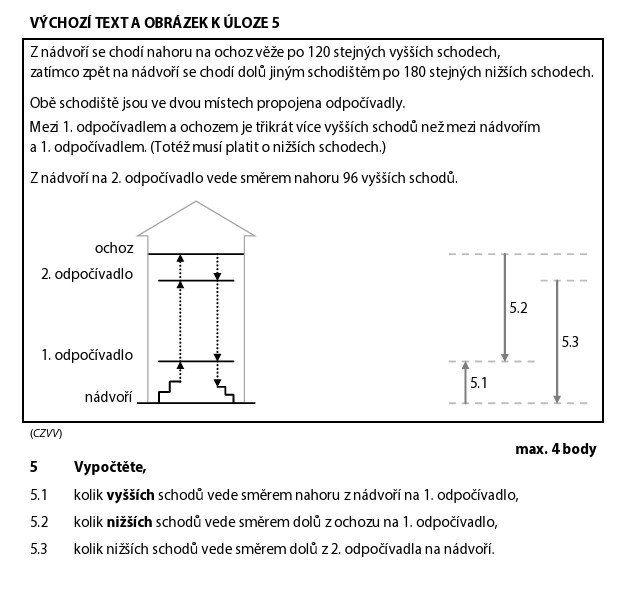
📋 Zadání — 2. náhradní termín, Úloha 5 (4 body)

Nahoru na ochoz věže vede 120 vyšších schodů, dolů 180 nižších schodů. Na schodišti jsou 2 odpočívadla. Mezi 1. odpočívadlem a ochozem je 3× více vyšších schodů než mezi nádvořím a 1. odpočívadlem. Z nádvoří na 2. odpočívadlo je 96 vyšších schodů.

5.1) Kolik vyšších schodů z nádvoří na 1. odpočívadlo?

5.2) Kolik nižších schodů z ochozu na 1. odpočívadlo?

5.3) Kolik nižších schodů z 2. odpočívadla na nádvoří?

1 5.1) Vyšší schody: nádvoří → 1. odpočívadlo

Celkem 120 vyšších schodů nahoru. Rozdělíme na 2 části:

Nádvoří → 1. odpočívadlo = 1 dílek

1. odpočívadlo → ochoz = 3 dílky (3× více)

Celkem: 1 + 3 = 4 dílky

120 : 4 = 30 vyšších schodů

2 5.2) Nižší schody: ochoz → 1. odpočívadlo

Z 1. odpočívadla na ochoz je 3 × 30 = 90 vyšších schodů.

Vyšší a nižší schody jsou v poměru: na 2 vyšší připadají 3 nižší.

90 vyšších schodů → 90 : 2 = 45 (to je 1 dílek)

45 × 3 = 135 nižších schodů

3 5.3) Nižší schody: 2. odpočívadlo → nádvoří

Z nádvoří na 2. odpočívadlo je 96 vyšších schodů.

Opět poměr 2 vyšší : 3 nižší:

96 : 2 = 48 (to je 1 dílek)

48 × 3 = 144 nižších schodů

✅ Výsledek

5.1) 30 5.2) 135 5.3) 144

💡 Tip pro CERMAT

Tady je klíč poměr vyšších a nižších schodů: celkem 120 vyšších a 180 nižších → poměr 120 : 180 = 2 : 3. Tento poměr platí na každém úseku schodiště!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 9 (2 body)

Na polici je 140 krabiček s čaji, poskládaných do sloupečků po 4. V 10 sloupcích jsou jen černé čaje, v ostatních sloupcích je 1 černý a 3 ovocné čaje. Kolik je ovocných čajů?

A) 30 B) 40 C) 75 D) 100 E) jiný výsledek

1 Kolik sloupečků celkem?

140 krabiček ve sloupcích po 4:

140 : 4 = 35 sloupečků

2 Kolik sloupečků s ovocnými čaji?

10 sloupečků má jen černé čaje. Zbytek má i ovocné:

35 − 10 = 25 sloupečků

3 Kolik ovocných čajů?

V každém z těchto 25 sloupečků jsou 3 ovocné čaje:

25 × 3 = 75 ovocných čajů

✅ Výsledek

C) 75 ovocných čajů

💡 Tip pro CERMAT

Pozor — nepočítej všechny čaje v 25 sloupcích (to by bylo 100), ale jen ovocné! Každý sloupeček má 1 černý + 3 ovocné. Otázka je na ovocné, ne na všechny.

📝 Oficiální řešení CERMAT

📋 Zadání — 2. náhradní termín, Úloha 13 (5 bodů)

Přiřaďte ke každé třídě správný počet chlapců:

13.1) 1. třída: 24 žáků, chlapců je 2× více než dívek.

13.2) 2. třída: 25 žáků. Bez 3 chlapců a 2 dívek bylo chlapců o 4 více než dívek.

13.3) 3. třída: chlapců je o pětinu méně než dívek, rozdíl je 3.

Možnosti: A) 12 B) 13 C) 14 D) 15 E) 16 F) jiný počet

1 13.1) Chlapců je 2× více než dívek

24 žáků, chlapců 2× více → poměr chlapci : dívky = 2 : 1

Celkem 3 dílky:

24 : 3 = 8 (1 dílek) → chlapců = 2 × 8 = 16 → E

2 13.2) Po odchodu 3 chlapců a 2 dívek...

Ze třídy odešli 3 chlapci a 2 dívky → zůstalo 25 − 5 = 20 přítomných

Z přítomných: chlapci o 4 více než dívky.

Rozdíl 4, součet 20 → chlapci: (20 + 4) : 2 = 12, dívky: (20 − 4) : 2 = 8

Ale to jsou přítomní! Celkem chlapců: 12 + 3 = 15

přítomní: 12 ch. + 8 d. → celkem chlapců: 12 + 3 = 15 → D

3 13.3) Chlapců o pětinu méně než dívek

⚠️ Pozor na chyták! „O pětinu méně" = pětina z dívek je rozdíl.

Pětina z dívek = 3 (to je ten rozdíl)

Dívek: 5 × 3 = 15

Chlapců: 15 − 3 = 12

Pětina dívek = 3 → dívek 15, chlapců 15 − 3 = 12 → A

✅ Výsledek

13.1) E (16) 13.2) D (15) 13.3) A (12)

💡 Tip pro CERMAT

Největší past je ve 13.3: „o pětinu méně" znamená, že rozdíl je pětina z většího čísla (dívek), ne pětina z celku! A ve 13.2 nezapomeň přičíst zpět ty, kteří odešli.

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Poměry a skupiny

Co si odnést z tohoto tématu

🧭 Strategie řešení

Najdi dílek — u poměrů rozděl celek na dílky a zjisti hodnotu jednoho dílku
Spočítej celkový počet skupin, pak obsah každé skupiny
U výběrových úloh ověř výsledek zpětným dosazením
Postupuj od toho, co znáš, k tomu, co hledáš

⚠️ Typické chytáky

„O pětinu méně" = rozdíl je pětina z většího čísla (ne pětina z celku!)
„Právě 3" = přesně 3, ne „alespoň 3" — každá skupina je stejná
„Bez 3 chlapců" — nezapomeň je na konci přičíst zpět
„2× více" — pozor: někdy to znamená poměr 2 : 1, jindy 3 : 1 (čti zadání pozorně!)

❌ Nejčastější chyby

Splést „o pětinu méně" s „pětina z celku"
Zapomenout přičíst zpět ty, kteří ve skupině chybí
U NSN úlohy: zapomenout, že se ptají na skupiny (ne na děti)
Nezkontrolovat, jestli celkový počet sedí po dosazení zpět

👥 Poměry a skupiny

🔑 Jak na poměry a skupiny?

🎯 Rady pro CERMAT: Poměry a skupiny