
Projdeme si všechny informace ze zadání:
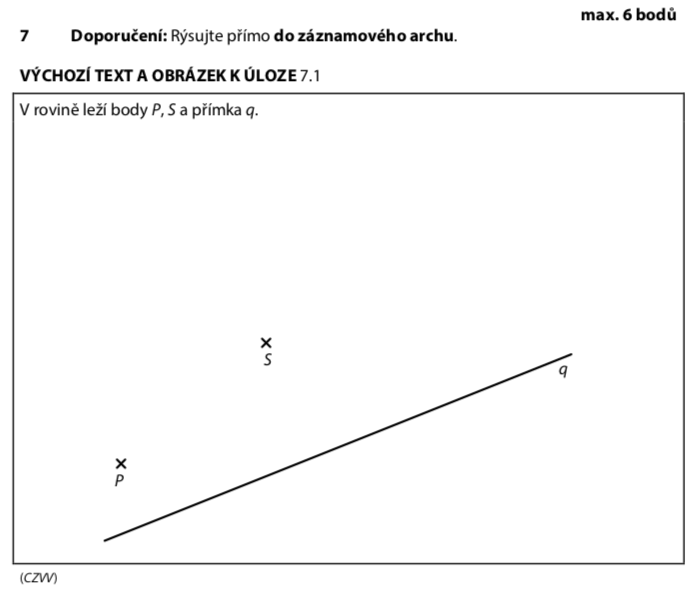
- Bod P — je dán, je to vrchol trojúhelníku
- Bod S — je dán, je to střed kružnice A ZÁROVEŇ střed strany QR
- Přímka q — na ní leží bod Q
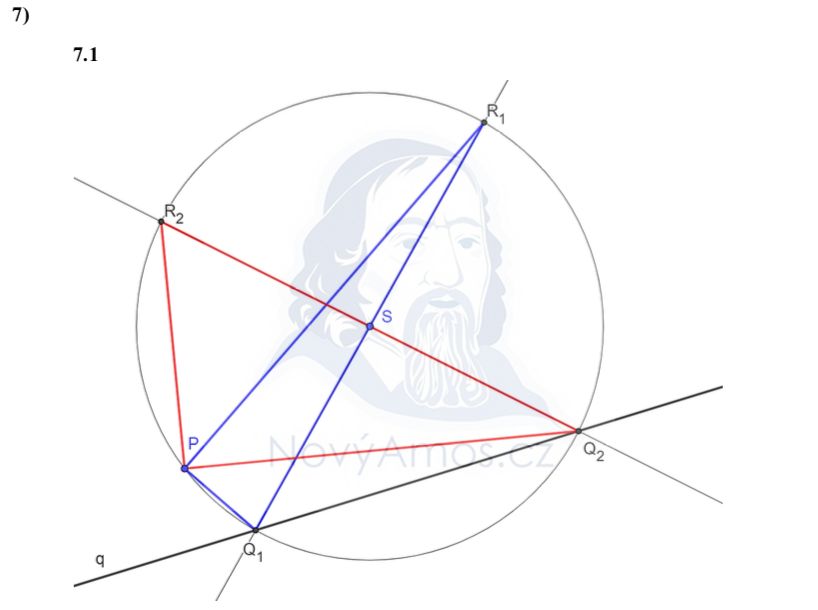
- P a Q leží na stejné kružnici se středem S → |SP| = |SQ|
Klíčové slovní spojení: „střed strany QR“ znamená, že S leží přesně uprostřed mezi Q a R.
P a Q leží na kružnici se středem S. Známe S a P, takže známe poloměr:
- Narýsujeme kružnici se středem S a poloměrem |SP|
- Q leží na přímce q A ZÁROVEŇ na kružnici → prúsečíky kružnice s přímkou q
- Kružnice protíná přímku ve 2 bodech → Q1 a Q2
Už máme dva možné body Q → 2 řešení!
S je střed strany QR — to znamená, že R leží na opačné straně od Q, stejně daleko od S:
- R leží na přímce QS, na druhé straně od Q
- Vzdálenost |SR| = |SQ| (S je střed)
- Prostě od S naměříme vzdálenost |SQ| na druhou stranu → bod R
Pro každé Q dostaneme jedno R → celkem 2 řešení.
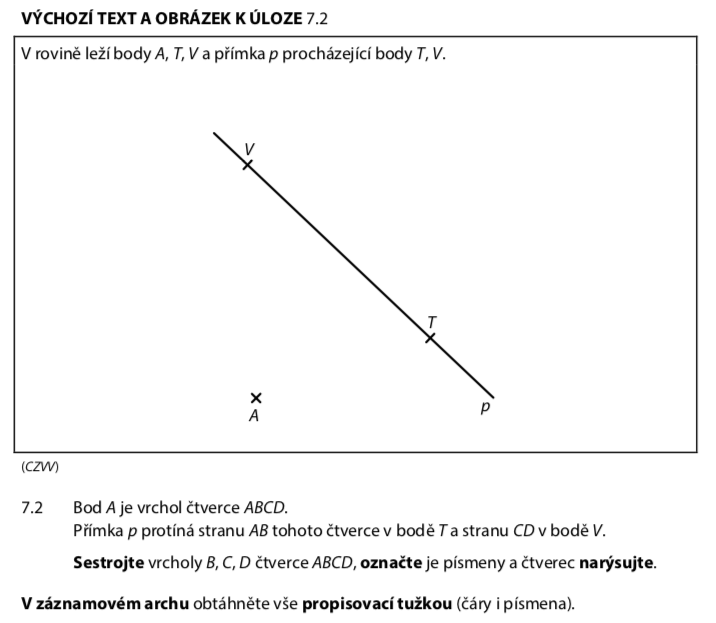
Máme dané:
- Bod A — vrchol čtverce
- Body T, V na přímce p: T leží na AB, V leží na CD
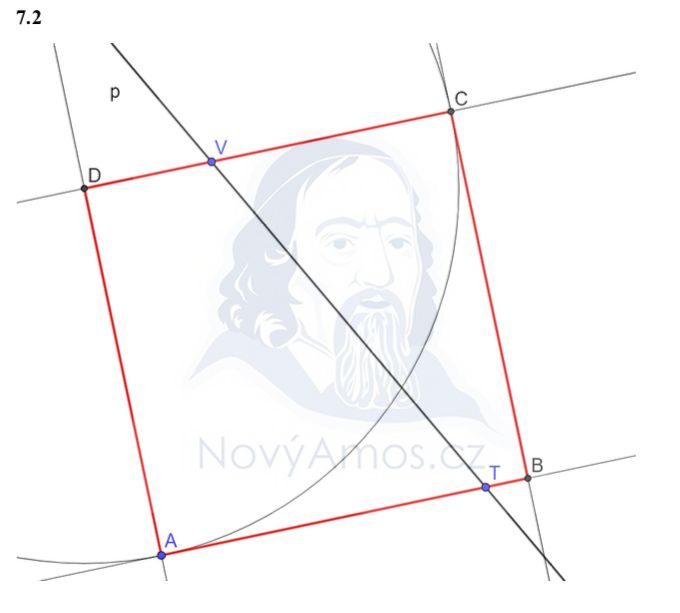
Přímka AB prochází bodem A a bodem T → rovnou máme směr strany AB!
Strana CD je rovnoběžná s AB (u čtverce jsou protější strany rovnoběžné). A prochází bodem V.
- Přímka AB prochází body A a T → narýsujeme ji
- Bodem V vedeme rovnoběžku s AB → to je přímka, na které leží CD
- Z bodu A sestrojíme kolmici k AB → přímka strany AD
- Prúsečík kolmice s přímkou CD je bod D
- |AD| je strana čtverce → na přímce AB naměříme |AB| = |AD| → bod B
- Z B vedeme kolmici → prúsečík s přímkou CD je bod C
Podle polohy bodú múže vycházet 1–2 řešení.
„Střed strany QR“ znamená, že S leží přesně uprostřed — stačí naměřit stejnou vzdálenost na druhou stranu a máš druhý konec!
- Kružnice + přímka = většinou 2 prúsečíky = 2 řešení
- U čtverce: protější strany jsou rovnoběžné, sousední jsou kolmé
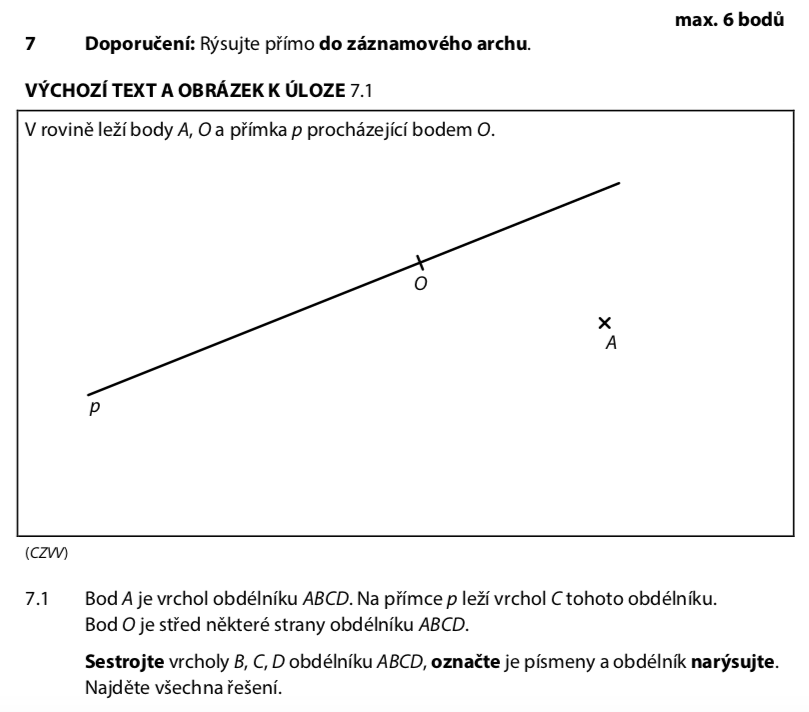

Projdeme si informace:
- Bod A — vrchol obdélníku, je dán
- Bod O — střed některé strany obdélníku
- Přímka p prochází bodem O — na ní leží bod C
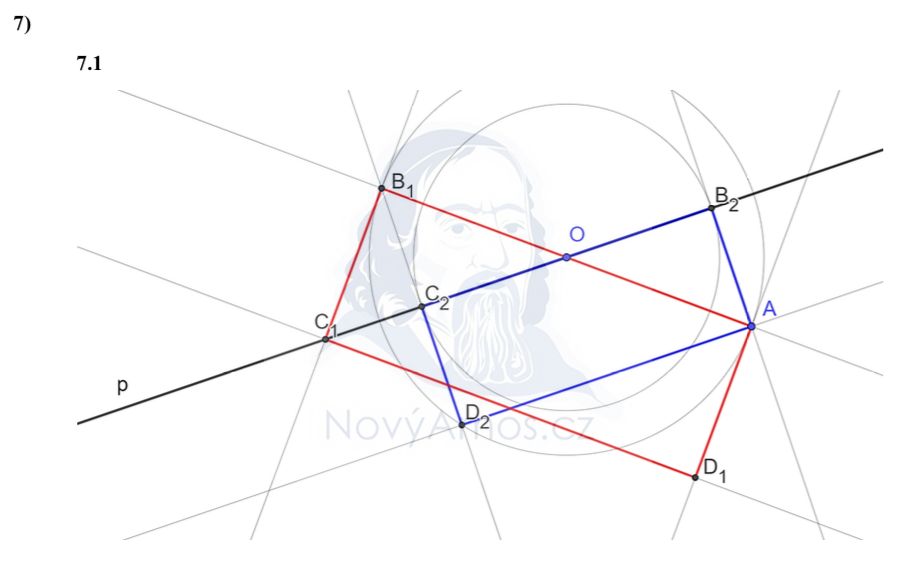
O je střed „některé strany“ — to znamená, že múže být středem rúzných stran. Každá varianta dá jiné řešení!
O múže být středem strany, na které leží A (např. AB nebo AD), nebo strany, na které A neleží (např. BC nebo CD).
- Pokud O je střed AB: bod B leží souměrně s A podle O → |AO| = |OB|
- Pokud O je střed AD: bod D leží souměrně s A podle O
- V obou případech pak C hledáme jako prúsečík s přímkou p
Každá varianta dá jinak orientovaný obdélník → 2 řešení.
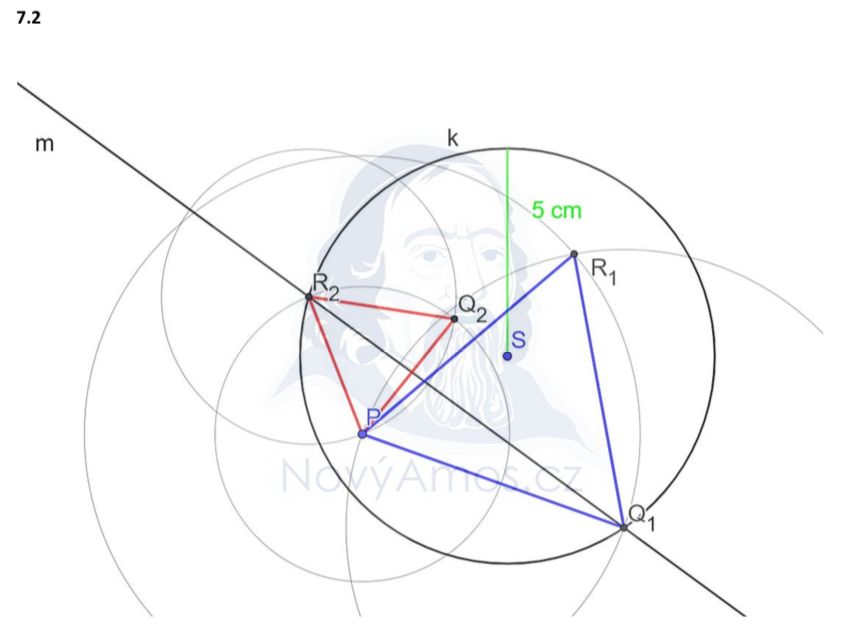
Pozor! Kružnice k má poloměr 5 cm, ale to neznamená, že strany trojúhelníku jsou 5 cm. Stranu neznáme — víme jen, že všechny tři jsou stejně dlouhé.
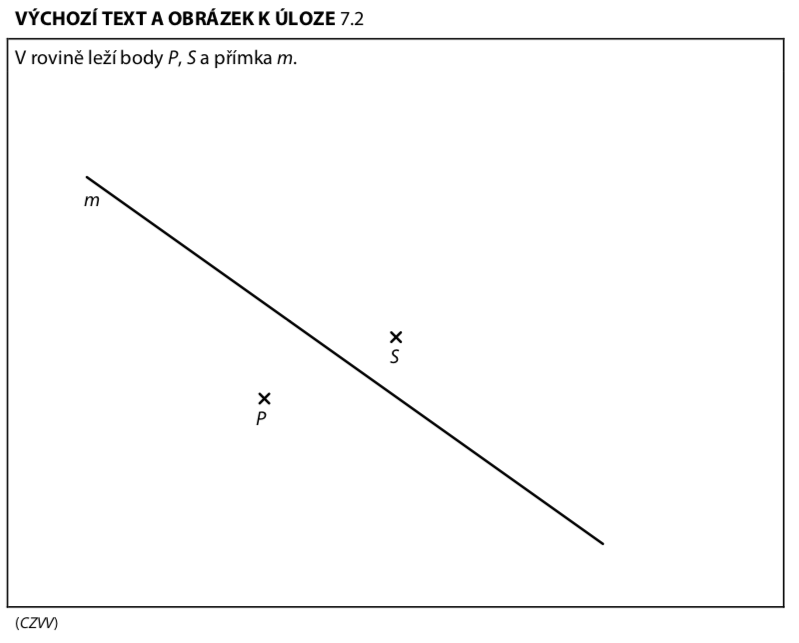
Co víme:
- P — vrchol trojúhelníku, je dán
- Další vrchol leží na přímce m a zároveň na kružnici k
- Třetí vrchol leží uvnitř kružnice k
- Narýsujeme kružnici k se středem S a r = 5 cm
- Hledáme bod Q (nebo R), který leží na m i na k → prúsečíky přímky m s kružnicí k
- Pro každý takový bod sestrojíme rovnostranný trojúhelník s vrcholem P
- Kružnici se středem v nalezeném bodě a poloměrem |P − nalezený bod| → prúsečík dá třetí vrchol
- Třetí vrchol musí ležet uvnitř k — to nám pomúže vybrat správné řešení
Vychází 2 řešení.
Když zadání říká „střed některé strany“, musíš vyzkoušet všechny možnosti! Každá varianta múže dát jiné řešení.
- Rovnostranný trojúhelník: všechny strany stejně dlouhé → stačí znát jednu stranu
- Podmínka „uvnitř kružnice“ ti pomúže vyřadit nesprávná řešení


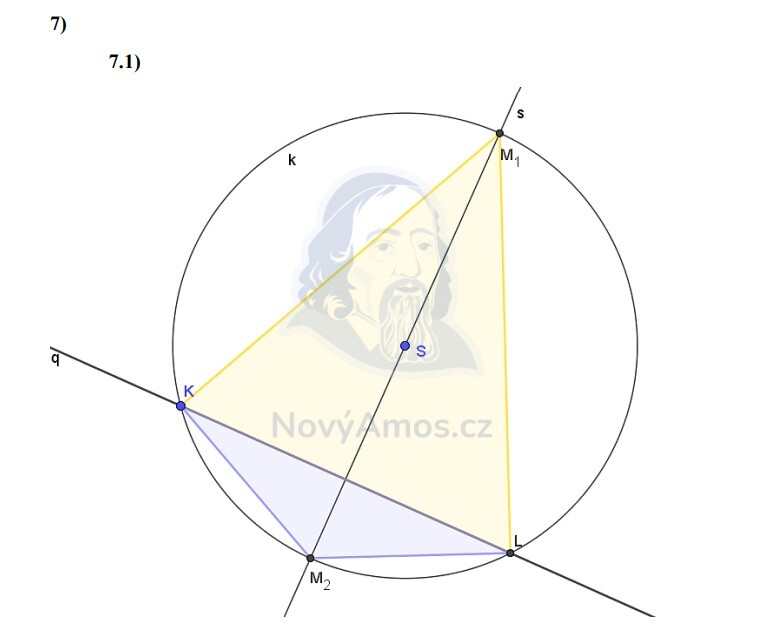
Všechny tři vrcholy leží na kružnici se středem S (opsaná kružnice). Známe K a S, takže:
- K leží na kružnici a na přímce q
- L leží na kružnici a na přímce q (druhý prúsečík!)
- M leží na kružnici a na přímce s (kolmé na q, procházející S)
- Narýsujeme kružnici se středem S a poloměrem |SK|
- Prúsečíky kružnice s přímkou q → jeden je K, druhý je bod L
- Bodem S vedeme kolmici s na přímku q
- Prúsečíky kružnice s přímkou s → dva možné body M
M múže být „nahoře“ nebo „dole“ → 2 řešení!
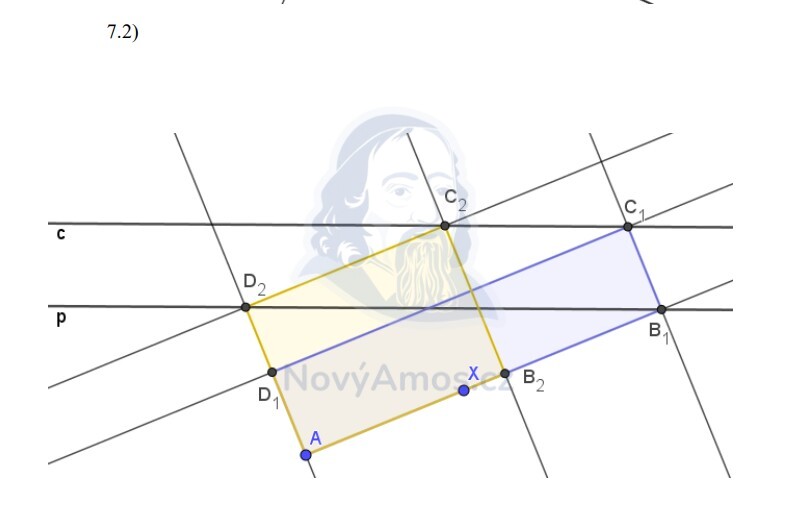
X leží uvnitř strany AB → přímka AB prochází body A a X. To nám dává směr strany AB!
- Narýsujeme přímku AX → na ní leží strana AB
- Z bodu A vedeme kolmici k AB → směr strany AD
- Prúsečík s přímkou p (nebo c) → další vrcholy
- C leží na přímce c → sestrojíme rovnoběžku s AB procházející nalezeným bodem
Podle vzájemné polohy přímek vychází 2 řešení.
Když vidíš v zadání „přímka kolmá“, použij trojúhelník s pravítkem. A pamatuj:
- Kružnice protíná přímku většinou ve 2 bodech
- Když jeden prúsečík už znáš (např. K), druhý je hledaný bod!
- Bod „uvnitř strany“ ti určuje směr té strany
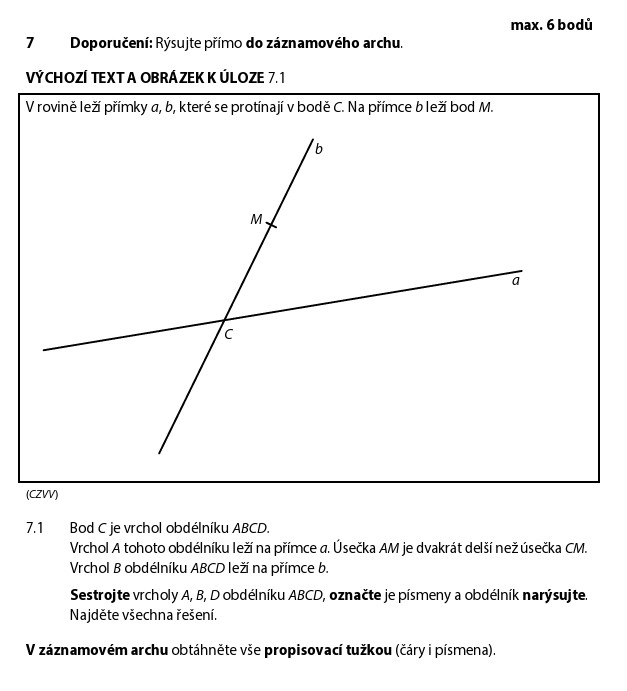
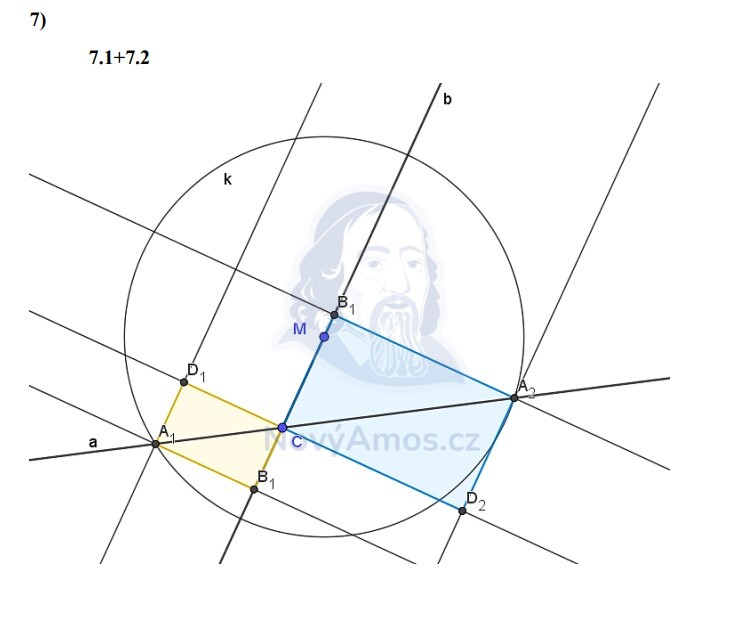
Přímky a a b se protínají v bodě C (vrchol obdélníku). Dále:
- A leží na přímce a
- B leží na přímce b
- M je dán na přímce b a platí: AM = 2 × CM
Podmínka AM = 2 × CM znamená, že A je od M dvakrát dál než C. Tady nám pomúže kružnice!
Vzdálenost |CM| známe (změříme). AM = 2 × CM, takže:
- Narýsujeme kružnici se středem M a poloměrem 2 × |CM|
- A leží na přímce a A ZÁROVEŇ na kružnici → prúsečíky
- Kružnice protíná přímku a ve 2 bodech → A1 a A2
Dva možné body A → 2 řešení!
Pro každý bod A:
- Strana AB je kolmá na stranu AD (pravý úhel u A)
- CB leží na přímce b → B = prúsečík kolmice z A na směr AD s přímkou b
- D sestrojíme pomocí rovnoběžek (AD ∥ BC, CD ∥ AB)
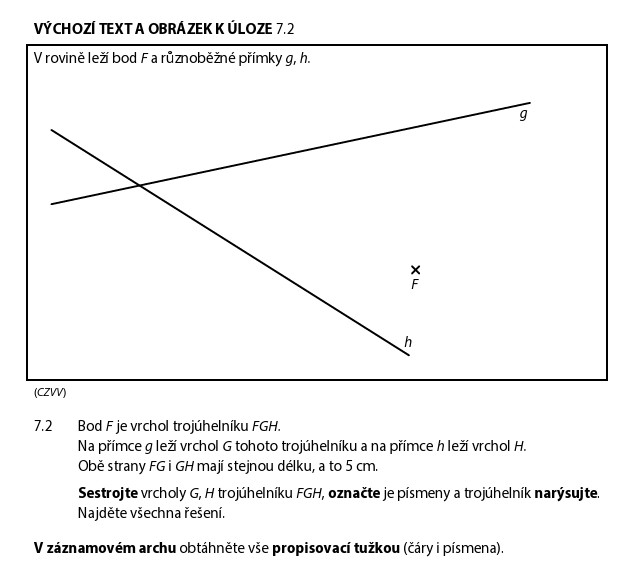
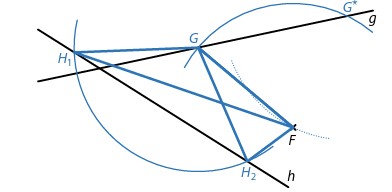
FG = GH = 5 cm (rovnoramenný trojúhelník z pohledu bodu G). Postup:
- Narýsujeme kružnici z F s poloměrem 5 cm
- G leží na přímce g a na kružnici → prúsečíky = možné body G
- Pro každé G: narýsujeme kružnici z G s poloměrem 5 cm
- H leží na přímce h a na této kružnici → prúsečíky = možné body H
Múže vycházet více řešení — záleží na poloze přímek.
Podmínka AM = 2 × CM znamená, že bod A leží na kružnici se středem M (ne se středem C!). Dávej pozor, který bod je střed.
- AM = 2 × CM → kružnice (M; 2·|CM|)
- FG = GH = 5 cm → dvě kružnice postupně (nejdřív z F, pak z G)
- Vždy nakonec napiš: „Úloha má X řešení“
🎯 Rady pro CERMAT: Geometrické konstrukce
Co si odnést z tohoto tématu
- Vždy hledej VŠECHNA řešení — u CERMATu jich bývá většinou 2
- Tvé hlavní nástroje: kružítko (kružnice = všechny body ve stejné vzdálenosti) a pravítko (přímky, kolmice, rovnoběžky)
- „Střed strany“ = bod uprostřed → naměř stejnou vzdálenost na druhou stranu
- U obdélníku: protější strany rovnoběžné, sousední kolmé
- Označ všechny vrcholy písmeny — CERMAT chce přesné označení
- Zapomenout na druhé řešení je chyba č. 1! Kružnice protíná přímku ve 2 bodech → 2 řešení
- „Střed strany“ znamená, že bod leží přesně uprostřed — ne „někde na straně“
- Podmínka AM = 2 × CM: dávej pozor, který bod je střed kružnice!
- „Některé strany“ = více variant → každá dává jiné řešení
- Najít jen jedno řešení a zapomenout na druhé (prohozené body)
- Nezapsat postup konstrukce — CERMAT dává body za zápis, ne jen za obrázek!
- Zapomenout ověřit, že body leží na správných přímkách
- Nepoužít strukturu: Dáno → Postup → Závěr
- Chybějící závěr: „Úloha má X řešení“ — bez něj přijdeš o body