Na miskách vah jsou koule, válce a závaží. Tři váhy jsou v rovnováze. Urči hmotnost jedné koule a jednoho válce.
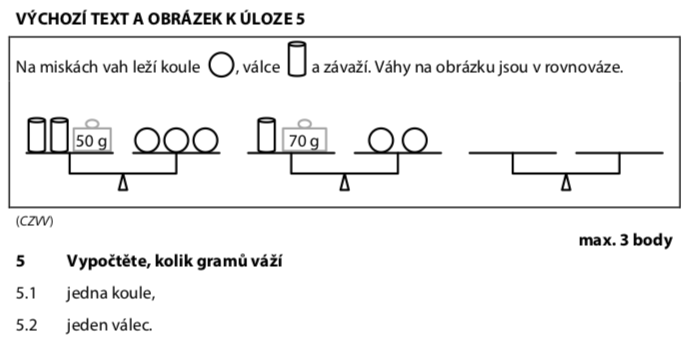
Ze zadání máme tři váhy v rovnováze. Klíčový trik: porovnáme dvoje váhy tak, aby nám vypadlo jedno neznámé.
Z rovnic vah postupně zjistíme vztah mezi koulí a válcem. Hledáme: kolik gramů váží 1 koule? A kolik 1 válec?
Trik s vahami: co odebereš z obou misek, rovnováha zůstane!
Postupným odebíráním a dosazováním zjistíme, že:
Když už víme, že koule = 90 g, dosadíme do jiných vah a dopočítáme válec:
Kontrola: dosadíme obě hodnoty do všech tří vah — všechny musí být v rovnováze. ✅
U vah si pamatuj zlaté pravidlo: co odebereš z obou stran, rovnováha zůstane. Hledej váhy, kde se dá něco „vykrátit“ — třeba stejné koule na obou stranách.

Na Dračí horu přiletěli dvouhaví a tříhlaví draci. Dohromady mají 115 hlav. Dvouhavých draků je o 35 více než tříhlavých.
Kolik draků přiletělo celkem?

Zkusme si představit, že dvouhavých a tříhlavých draků je stejně. Kolik by jich bylo?
Jeden „pár“ (1 dvouhavý + 1 tříhlavý) má dohromady 2 + 3 = 5 hlav.
Takže: 23 dvouhavých a 23 tříhlavých — ale rozdíl je 0, a my potřebujeme rozdíl 35!
Potřebujeme zvětšit rozdíl na 35 a přitom zachovat 115 hlav.
Jak? Přidáme 3 dvouhavé (+ 6 hlav) a ubereme 2 tříhlavé (− 6 hlav). Hlavy se nezmění!
Kolikrát musíme tuhle výměnu udělat?
Za 7 výměn přibude 7 × 3 = 21 dvouhavých a ubude 7 × 2 = 14 tříhlavých:
Kontrola rozdílu: 44 − 9 = 35 ✅
Kontrola hlav: 44 × 2 + 9 × 3 = 88 + 27 = 115 ✅
Tohle je klasická „Cermatovina“! U dračích úloh: začni jako by bylo stejně obou druhů, pak přesouvej tak, aby se počet hlav nezměnil. Pozor: „o 35 více“ = rozdíl, ne celkový počet!

4 běžci: Eda, Leoš, Adam a Honza. Eda nebyl 1. ani poslední. Leoš doběhl těsně před Adamem. Adam doběhl později než Honza. Jaké bylo pořadí?
Na výletě bylo 5× více dětí než dospělých. Dospělých bylo o 60 méně než dětí. Kolik bylo dětí?

„Těsně před“ znamená, že Leoš a Adam běželi hned za sebou — L, A.
Adam doběhl později než Honza → Honza je před Adamem.
Eda nebyl 1. ani poslední → Eda je 2. nebo 3.
Leoš-Adam musí být spolu (LA). Honza je před Adamem. Eda není 1. ani 4.
Zkusíme: H, E, L, A
Kontrola: Eda není 1. ani poslední ✅ Leoš těsně před Adamem ✅ Adam později než Honza ✅
Dětí je 5× více než dospělých. Nakreslíme si to pomocí dílků:
Rozdíl: 5 − 1 = 4 dílky = 60 osob
Dospělých: 1 × 15 = 15. Dětí: 5 × 15 = 75.
Kontrola: 75 − 15 = 60 ✅ a 75 : 15 = 5 ✅
U pořadí: začni dvojicí, která musí být spolu (Leoš-Adam), a pak ji zasaď do řady podle ostatních podmínek. U dílkových úloh: „5× více“ = poměr 5 : 1, rozdíl je 4 dílky!

Na hradě žijí dvouhaví a tříhlaví draci. Celkem je 52 draků a 134 hlav.

Kdybychom měli stejně obou druhů: 26 dvouhavých a 26 tříhlavých.
Kolik by bylo hlav?
Ale my potřebujeme 134 hlav — chybí nám 4 hlavy!
Když vyměníme 1 dvouhavého za 1 tříhlavého:
• Počet draků se nezmění (pořád 52)
• Počet hlav se zvýší o 1 (3 − 2 = 1)
Potřebujeme přidat 4 hlavy → vyměníme 4 draky:
Kontrola: 22 + 30 = 52 ✅ 22×2 + 30×3 = 44 + 90 = 134 ✅
Hlavy tříhlavých: 30 × 3 = 90
Hlavy dvouhavých: 22 × 2 = 44
Všimni si, že tady známe celkový počet draků (ne rozdíl). Takže začínáme „půl na půl“ a přesouvej draky po jednom. Každá výměna změní počet hlav o 1!

Stejné dlaždice na paletách. Plná paleta = 10 dlaždic.
• 2 plné palety váží 340 kg
• 1 paleta + 4 dlaždice váží 80 kg

Informace 1: 2 palety + 20 dlaždic = 340 kg (protože každá plná paleta má 10 dlaždic)
Informace 2: 1 paleta + 4 dlaždice = 80 kg
Trik: zdvojnásobíme informaci 2, abychom měli stejný počet palet!
Takže: 2 palety + 8 dlaždic = 160 kg
Obečteme od sebe obě rovnice (obě mají 2 palety):
(Protože 20 − 8 = 12 dlaždic)
Z informace 2: 1 paleta + 4 dlaždice = 80 kg
Kontrola: 2 × (20 + 10 × 15) = 2 × (20 + 150) = 2 × 170 = 340 ✅
Tohle je stejný trik jako u vah: uprav rovnice tak, aby něco měly společného (třeba 2 palety). Pak odečti a jedno neznámé ti zmizí. Super metoda pro 5. třídu — žádné rovnice, jen chytré odečítání!

🎯 Rady pro CERMAT: Logické úlohy
Co si odnést z tohoto tématu
- U vah — odeber stejné z obou stran, rovnováha zůstane. Hledej, co se dá „vykrátit“.
- U draků — začni jako by bylo stejně obou druhů, pak přesouvej po jednom (nebo po skupinách).
- U pořadí — začni dvojicí, která musí být spolu, a zasaď ji do řady.
- U dlaždic/palet — uprav rovnice tak, aby měly něco společného, pak odečti.
- „o 35 více“ = rozdíl, ne celkový počet! Pozor na to, co přesně je víc.
- „5× více“ = poměr 5 : 1. Rozdíl je pak 4 dílky, ne 5!
- „Těsně před“ = hned za sebou, bez mezery. To omezuje možnosti!
- U vah: nezapomeň, že paleta též něco váží — nepočítej jen dlaždice.
- Splést počet draků s počtem hlav — výsledek se ptá na draky, ne na hlavy!
- U vah/palet zapomenout zkontrolovat obě rovnice po dosazení výsledku.
- U pořadí přehlédnout podmínku „nebyl 1. ani poslední“ — obě části platí!
- Spokojit se s prvním výsledkem a neověřit ho zpětným dosazením.