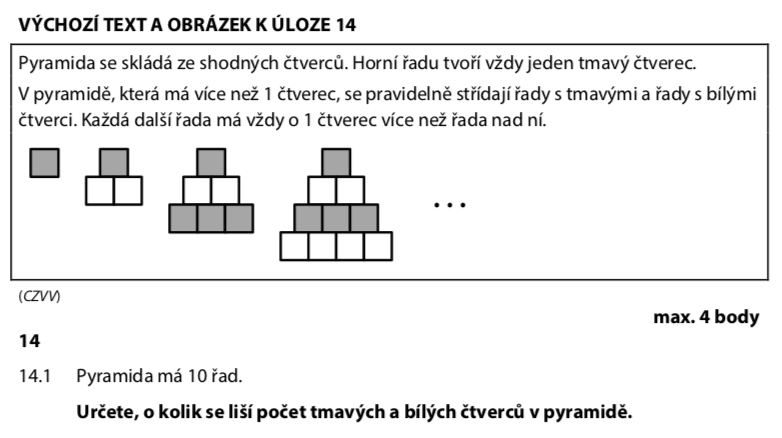

Pyramida roste shora dolů. 1. řada (nahoře) = 1 čtverec, 2. řada = 2 čtverce, 3. řada = 3 čtverce...
Barvy se střídají po řadách: 1. řada je tmavá, 2. bílá, 3. tmavá, 4. bílá...
Liché řady (1., 3., 5., ...) jsou tmavé. Sudé řady (2., 4., 6., ...) jsou bílé.
Spočítáme tmavé čtverce (liché řady) a bílé čtverce (sudé řady):
Bílých je víc! Rozdíl:
💡 Všimni si: rozdíl = 10 : 2 = 5. To není náhoda!
Pojďme se podívat na to pravidlo. Každá sudá řada má o 1 čtverec víc než lichá řada před ní:
| Dvojice řad | Tmavá | Bílá | Rozdíl |
|---|---|---|---|
| 1. a 2. | 1 | 2 | +1 pro bílou |
| 3. a 4. | 3 | 4 | +1 pro bílou |
| 5. a 6. | 5 | 6 | +1 pro bílou |
| 7. a 8. | 7 | 8 | +1 pro bílou |
| 9. a 10. | 9 | 10 | +1 pro bílou |
Při sudém počtu řad je rozdíl = počet dvojic = počet řad : 2. Bílých je víc.
Při lichém počtu řad poslední lichá řada převáží — tmavých je víc. Rozdíl = (počet řad + 1) : 2.
73 je liché číslo → poslední řada je tmavá → tmavých je víc.
Použijeme naše pravidlo:
Tmavých čtverců je o 37 víc než bílých.
Bílých je méně → tmavých je víc → počet řad je lichý.
Rozdíl = (počet řad + 1) : 2 = 101. Zpátky:
Pyramida má 201 řad.
U pyramidy se střídajícími barvami:
- Sudý počet řad: rozdíl = počet řad : 2 (bílých víc)
- Lichý počet řad: rozdíl = (počet řad + 1) : 2 (tmavých víc)
- Nemusíš sčítat všechny řady — stačí znát pravidlo a použít zkratku!


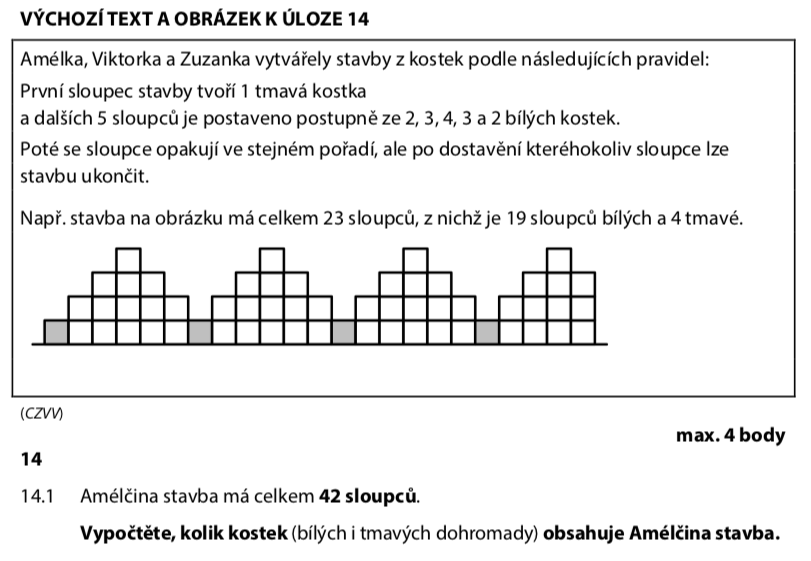

Vzor se opakuje každých 6 sloupců:
Každých 6 sloupců: výšky 1, 2, 3, 4, 3, 2 → celkem kostek v jednom cyklu:
Z toho: 1 tmavá kostka + 14 bílých kostek. A 1 tmavý sloupec + 5 bílých sloupců.
Kolikrát se vejde celý cyklus (6 sloupců) do 42 sloupců?
Každý cyklus má 15 kostek:
V každém cyklu je 5 bílých sloupců a 1 tmavý. Kolik celých cyklů se vejde do 58 bílých sloupců?
To znamená: 11 úplných cyklů (každý má 1 tmavý sloupec) + 3 další bílé sloupce. Ale po 11. cyklu začíná 12. tmavý sloupec, a za ním 3 bílé.
Tmavých sloupců (= tmavých kostek) je tedy:
💡 Každý tmavý sloupec má jen 1 kostku, takže 12 tmavých sloupců = 12 tmavých kostek.
Kolik celých cyklů se vejde do 156 kostek?
10 celých cyklů = 10 × 6 = 60 sloupců a 10 × 15 = 150 kostek.
Zbývá 156 − 150 = 6 kostek. Projdeme začátek dalšího cyklu:
| Sloupec | Výška | Kumulativně |
|---|---|---|
| 61. (tmavý) | 1 | 1 |
| 62. | 2 | 3 |
| 63. | 3 | 6 ✅ |
Přesně 6 kostek — to sedí! Celkem sloupců:
U staveb z kostek s opakujícím se vzorem:
- Nejdřív zjisti délku cyklu (počet sloupců) a počet kostek v cyklu
- Vyděl se zbytkem — celé cykly plus zbytek
- Pozor: když zbyde část cyklu, musíš sloupce postupně přičítat, dokud nesedí
- Zbytek = 0 znamená, že poslední cyklus končí přesně!



Začínáme na 51 436. Každou sekundu +1. Běží to 10 hodin. Kolik je to sekund?
Poslední číslo na displeji:
Hledáme palindromy v rozsahu 51 436 až 87 436.
Palindrom je číslo, které se čte stejně zepředu i zezadu. Například: 12321, 54345, 78987.
Pětimistný palindrom má tvar: ABCBA
První cifra = poslední cifra, druhá = čtvrtá. Prostřední může být jakákoli.
Začínáme od 51 436 a jdeme nahoru. Palindrom začínající na 5 má tvar 5_?_5.
Druhá cifra musí být stejná jako čtvrtá. Zkusíme 51?15:
51 015 až 51 415 jsou menší než 51 436, takže nespadá do rozsahu! První palindrom v rozsahu je:
Jdeme od 87 436 směrem dolů. Palindrom začínající na 8 má tvar 8_?_8.
Zkusíme 87?78:
87 478 je větší než 87 436, takže už nespadá do rozsahu! Největší palindrom je:
Palindromy — oblíbený typ úlohy!
- Nejdřív urči rozsah čísel (začátek + doba × krok)
- Pětimistný palindrom ABCBA: stačí zvolit A, B a C — zbytek se doplní
- Pro nejmenší: začni od začátku rozsahu a jdi nahoru
- Pro největší: začni od konce rozsahu a jdi dolů
- Ověř si, že výsledek leží v rozsahu!


Když máme n bodů na přímce, z každého bodu vedeme šikmé čáry. Vznikne trojuhelnikový vzor — jako pyramida.
Počet černých puntíků v řadách: 1, 2, 3, ..., n. Celkem černých:
Ale je to ještě jednodušší — počet černých puntíků = n² (druhá mocnina počtu bodů).
Počet vodorovných přímek = 2n − 1 (rovnoběžky procházející řadami).
Ve spodní řadě je celkem 2n − 1 puntíků, z toho 1 černý a zbytek bílých.
Počet černých = n². Jaké n dává 36?
Máme 6 bodů na přímce. Počet vodorovných přímek:
Počet vodorovných přímek = 2n − 1 = 49.
Ve spodní řadě je celkem 2 × 25 − 1 = 49 puntíků. Z toho je 1 černý, takže bílých je:
Ve spodní řadě je 64 bílých + 1 černý = 65 puntíků celkem.
Počet černých puntíků celkem:
💡 Trik na počítání: 33 × 33 = 30 × 33 + 3 × 33 = 990 + 99 = 1 089.
U geometrických vzorů s body na přímce:
- Zapamatuj si: n bodů → n² černých a 2n − 1 přímek
- Druhé mocniny se hodí znát nazpaměť: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100...
- Ve spodní řadě: celkový počet minus 1 černý = bílé
- Když číslo není druhá mocnina, něco je špatně — zkontroluj!



Řada začíná:
Každá trojice má tvar: k, k+1, k+2, kde k začíná na 0 a roste o 1.
Trojice číslo t (počítáme od 1) začíná číslem t − 1.
Číslo 12 se poprvé objeví na poslední pozici trojice, která končí číslem 12.
Trojice končící číslem 12 začíná číslem 10: 10, 11, 12. To je 11. trojice (začíná číslem 10 = t − 1 → t = 11).
Na jakém místě je 3. člen 11. trojice?
Číslo 12 je poprvé na 33. místě.
Prvních 125 členů = kolik celých trojic + zbytek?
To je 41 celých trojic + 2 členy ze 42. trojice.
Podívejme se na vzor lichých a sudých čísel v trojicích:
| Trojice | Čísla | Lichá? | Počet lichých |
|---|---|---|---|
| 1. | 0, 1, 2 | S, L, S | 1 |
| 2. | 1, 2, 3 | L, S, L | 2 |
| 3. | 2, 3, 4 | S, L, S | 1 |
| 4. | 3, 4, 5 | L, S, L | 2 |
| Každé 2 trojice | 3 lichá | ||
V každých 2 trojicích (= 6 členech) jsou 3 lichá čísla.
41 trojic: 41 = 20 × 2 + 1 (20 celých párů + 1 trojice navíc).
41. trojice (lichá pořadím) začíná sudým číslem (40) → vzor S, L, S → 1 liché číslo.
Zbývají 2 členy ze 42. trojice: 41, 42. Z toho 41 je liché.
Která trojice a který člen?
152. místo = 2. člen 51. trojice.
51. trojice začíná číslem 51 − 1 = 50, takže trojice je: 50, 51, 52.
2. člen je:
U řad z opakujících se skupin:
- Zjisti délku skupiny a vyděl se zbytkem
- Zbytek = 0 znamená poslední člen předchozí skupiny (ne první člen další!)
- U lichých/sudých čísel: hledej vzor v párech trojic (opakuje se každých 6 členů)
- Všdy si ověř na prvních pár členech, že tvoje pravidlo funguje!

🎯 Rady pro CERMAT: Vzory a posloupnosti
Co si odnést z tohoto tématu
- Najdi opakující se vzor (periodu) — kolik prvků se opakuje?
- Vyděl celkový počet délkou periody → dostaneš celé cykly + zbytek
- Zbytek řeš ručně — projdi poslední neuplnou periodu po jednom
- U pyramidy se střídajícími barvami: hledej zkratkový vzorec místo sčítání
- Druhé mocniny (1, 4, 9, 16, 25, 36...) se hodí znát nazpaměť
- Chyba o jedničku (off-by-one): začínáš počítat od 0 nebo od 1? Ověř si na malém příkladu!
- Zbytek = 0 znamená, že jsme přesně na konci posledního cyklu — ne na začátku nového!
- CERMAT míchá počet sloupců vs. počet kostek — dávej pozor, co se ptá
- Palindromy: ověř si, že výsledek leží v daném rozsahu!
- Liché/sudé počty řad v pyramidě — každý má jiný vzorec pro rozdíl
- Zapomenout na zbytek po dělení — ten rozhoduje o výsledku!
- Spočítat periodu špatně (zapomenout na první nebo poslední prvek)
- U trojic: započítat pozici od 0 místo od 1 (nebo naopak)
- Nepřevést jednotky (hodiny na sekundy, minuty na sekundy...)
- Neověřit si pravidlo na prvních pár členech — vždy zkontroluj!