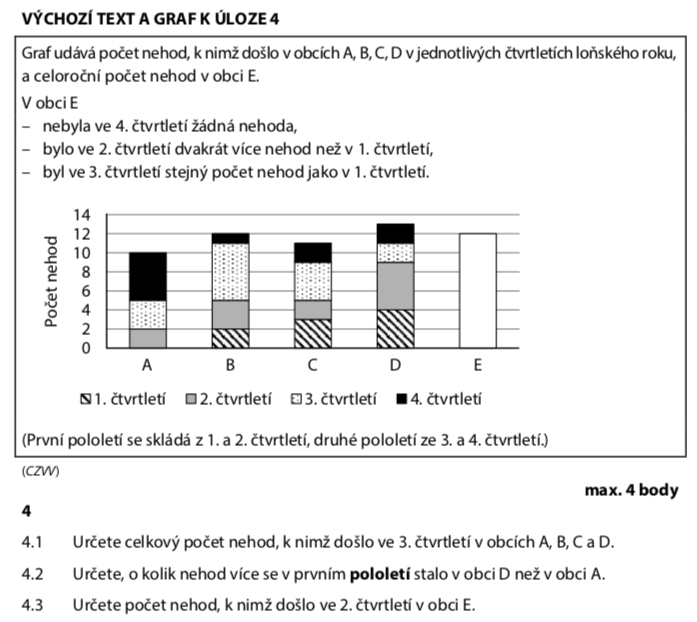
Z grafu si pečlivě přečteme počty nehod v jednotlivých čtvrtletích:
| Obec | 1. čtvrt. | 2. čtvrt. | 3. čtvrt. | 4. čtvrt. |
|---|---|---|---|---|
| A | 0 | 2 | 3 | 1 |
| B | 3 | 2 | 6 | 5 |
| C | 2 | 5 | 4 | 3 |
| D | 4 | 5 | 2 | 1 |
Zvýrazněné hodnoty budeme potřebovat pro otázku 4.1!
Vezmeme zvýrazněné hodnoty ze 3. čtvrtletí:
Ve 3. čtvrtletí se v obcích A–D stalo celkem 15 nehod.
1. pololetí = 1. čtvrtletí + 2. čtvrtletí. Spočítáme pro obě obce:
V obci D se v 1. pololetí stalo o 7 nehod více než v obci A.
Ze zadání víme o obci E:
- 4. čtvrtletí = 0 nehod
- 2. čtvrtletí = 2× více než 1. čtvrtletí
- 3. čtvrtletí = stejně jako 1. čtvrtletí
- Celkem = 12 nehod
Řekněme, že v 1. čtvrtletí bylo X nehod. Pak:
Takže: 1. čtvrt. = 3, 2. čtvrt. = 2 × 3 = 6, 3. čtvrt. = 3, 4. čtvrt. = 0
💡 Nepoužíváme rovnice! Představ si, že máš 12 nehod rozdělit do 4 stejných dílků (protože X+2X+X+0 = 4 dílků). Jeden dílek = 12 : 4 = 3.
Když zadání říká "2× více" a "stejně", zkus si to představit pomocí dílků:
- 1. čtvrtletí = 1 dílek
- 2. čtvrtletí = 2 dílky (dvojnásobek)
- 3. čtvrtletí = 1 dílek (stejně jako 1.)
- 4. čtvrtletí = 0 dílků
- Celkem = 4 dílky = 12 → jeden dílek = 3

| Po | Út | St | Čt | Pá | Celkem | |
|---|---|---|---|---|---|---|
| 1. týden | 3 | 0 | 5 | 2 | 2 | 12 |
| 2. týden | 6 | 3 | 0 | 2 | 7 | 18 |
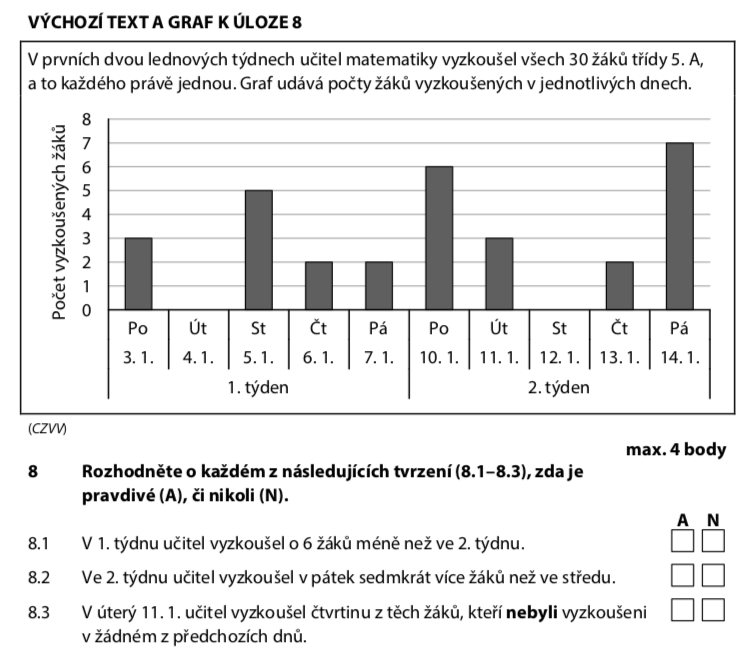
Nejdřív sečteme žáky v každém týdnu:
Ano, v 1. týdnu vyzkoušel o 6 méně. A — pravdivé
Pátek 2. týdne = 7 žáků. Středa 2. týdne = 0 žáků.
Tvrzení říká: "7× více žáků." Počítáme:
Cokoliv krát nula je pořád nula! Sedm není nula. N — nepravdivé
⚠️ Toto je typický chyták CERMATu! Když je jedno číslo nula, tak "×krát více" nemůže nikdy vyjít jinak než 0.
Úterý 2. týdne (11. 1.) — kolik žáků bylo do té doby vyzkoušeno?
Celý 1. týden + pondělí 2. týdne:
Celkem je 30 žáků. Kolik ještě zbývá?
V úterý 2. týdne vyzkoušel 3 žáky. Je to čtvrtina z 12?
Ano! 3 = čtvrtina z 12. A — pravdivé
Násobení nulou je past! Když je v grafu hodnota 0, tak:
- 7× více než 0 = 7 × 0 = 0 (NE 7!)
- Třikrát více než 0 = 3 × 0 = 0
- Nulu nemůžeš "znásobit" na nenulové číslo
U otázky 8.3 si musíš přesně spočítat, kolik žáků bylo vyzkoušeno PŘED daným dnem.

| Druh | 🛒 Zakoupené | 🌱 Vzrostlé | 💰 Prodané |
|---|---|---|---|
| A | 14 | 12 | 7 |
| B | 9 | 9 | 9 |
| C | 8 | 8 | 4 |
| D | 11 | 8 | 8 |
| Celkem | 42 | 37 | 28 |
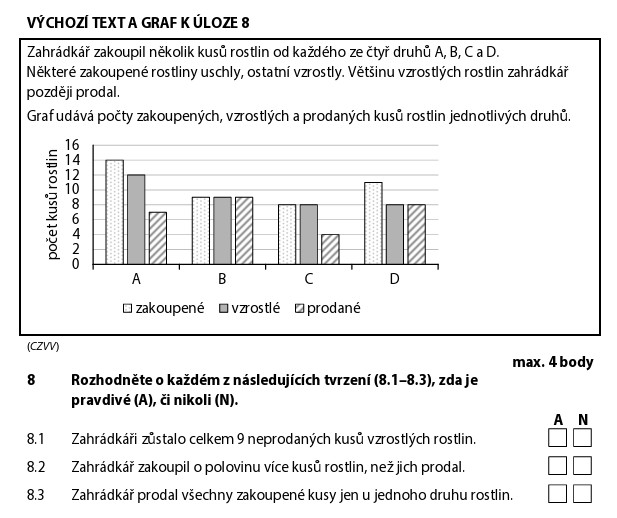
"Neprodané vzrostlé" = vzrostlé minus prodané. Spočítáme pro každý druh:
| Druh | 🌱 Vzrostlé | 💰 Prodané | Neprodané vzrostlé |
|---|---|---|---|
| A | 12 | 7 | 5 |
| B | 9 | 9 | 0 |
| C | 8 | 4 | 4 |
| D | 8 | 8 | 0 |
| Celkem | 9 |
Zůstalo mu přesně 9 neprodaných vzrostlých. A — pravdivé
Zakoupené = 42, prodané = 28.
Tvrzení říká: "Zakoupil o polovinu více, než prodal." To znamená:
Ano! 28 + polovina z 28 = 42. Souhlasí! A — pravdivé
⚠️ Pozor: "o polovinu více" znamená, že polovina se počítá z menšího čísla (z prodaných = 28), ne z většího!
Hledáme druhy, kde zakoupené = prodané:
| Druh | 🛒 Zakoupené | 💰 Prodané | Shoda? |
|---|---|---|---|
| A | 14 | 7 | ❌ ne |
| B | 9 | 9 | ✅ ano |
| C | 8 | 4 | ❌ ne |
| D | 11 | 8 | ❌ ne |
Pouze u druhu B prodal všechny zakoupené (9 = 9). To je právě 1 druh. A — pravdivé
Rozlišuj pojmy:
- "O polovinu více" = menší číslo + polovina menšího = větší číslo
- "Polovinu z" = prostě číslo : 2
- "Právě u jednoho druhu" = musíš zkontrolovat VŠECHNY druhy, aby ses ujistil/a, že je to opravdu jen jeden

Standa má o polovinu méně kartiček než Tomáš. Oba dohromady mají 24 kartiček. Petr má o 5 kartiček více než Radek.
A) 1 B) 8 C) 10 D) 17 E) jiný výsledek

Ze zadání: Standa má o polovinu méně než Tomáš a oba dohromady 24.
"O polovinu méně" znamená, že Standa má polovinu Tomáše. Představ si to pomocí dílků:
- Tomáš = 2 dílky
- Standa = 1 dílek (polovina Tomáše)
- Dohromady = 3 dílky = 24 kartiček
Tomáš má v grafu 3 dílky a vypočítali jsme, že má 16 kartiček... Hmm, to nesedí na celé číslo.
Ale Radek má v grafu 4 dílky. A z Tomáše víme, že 3 dílky = 16, takže pojďme jinak.
Podívejme se: Tomáš má 3 dílky = 16, tak 1 grafový dílek nemusí být celé číslo. Ale Radek má 4 dílky.
Ve skutečnosti graf ukazuje, že Radek má přesně 4 dílky. Protože Tomáš = 16 a má 3 dílky, jeden dílek ≈ 5,3... To ale znamená, že graf má jiné měřítko.
Zkusme to jinak: z grafu je vidět, že 1 dílek = 5 kartiček.
Petr má o 5 více než Radek:
A teď porovnáme Petra a Standu:
Petr má o 17 kartiček více než Standa.
U grafových úloh s neúplnými údaji postupuj takto:
- Nejdřív dopočítej chybějící hodnoty ze slovních podmínek
- Pak teprve odečti měřítko grafu (kolik je 1 dílek)
- "O polovinu méně" = polovina z většího. Když Tomáš a Standa mají dohromady 24 a Standa = polovina Tomáše, rozděl 24 na 3 dílky

🎯 Rady pro CERMAT: Čtení grafů
Co si odnést z tohoto tématu
- Nejdřív si přečti PŘESNÉ hodnoty z grafu a zapiš si je
- U každého A/N tvrzení spočítej — nikdy neodhaduj!
- Pozor na osy a měřítko — kolik znamená jeden dílek?
- Když chybí údaje, dopočítej je ze slovního zadání
- U trojitých grafů (zakoupené/vzrostlé/prodané) si pohlídej, které sloupce porovnáváš
- "7× více než 0" = 7 × 0 = 0 (ne 7!) — cokoliv krát nula je nula!
- "O polovinu více" — polovina se počítá z MENŠÍHO čísla (z původního)
- "O polovinu méně" — polovina se počítá z VĚTŠÍHO čísla
- Pozor: "o polovinu více" a "polovinu z" jsou dvě různé věci!
- Neúplné grafy — musíš dopočítat hodnoty z textu zadání
- Zapomenout zkontrolovat, jestli je hodnota v grafu nula — násobení nulou je past
- Splést si "o polovinu více" a "dvakrát tolik" (nejsou totéž!)
- Nečíst pozorně, které sloupce/řádky se mají sčítat
- U neúplných grafů přehlédnout slovní podmínky v zadání
- Hádat místo počítat — u CERMATu se musí počítat přesně