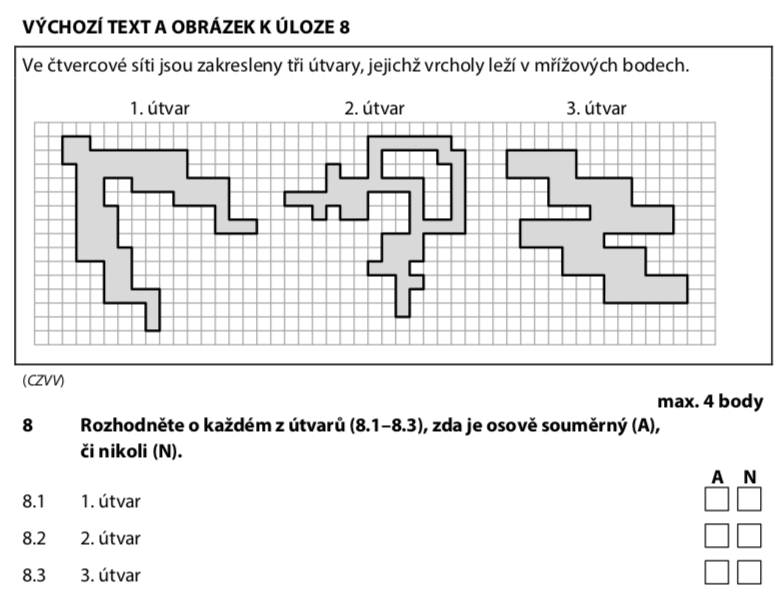
8.1) Je útvar 1 osově souměrný?
8.2) Je útvar 2 osově souměrný?
8.3) Je útvar 3 osově souměrný?
Představ si, že útvar přeložíš napůl podél nějaké čáry (osy). Pokud se obě poloviny přesně překryjí, je osově souměrný.
Důležité: osa nemusí být jen vodorovná nebo svislá — může být i šikmá (úhlopříčná)!
Příklad šikmé osy:
·───· Přeložíš přes úhlopříčku
│╲ │ a obě půlky se překryjí ✅
│ ╲│
·───·
Podíváme se na útvar 1 a zkusíme najít osu, podél které by se obě půlky přesně překryly.
Zkusíme šikmou osu z levého horního do pravého dolního rohu. Obě půlky se překryjí!
Zkusíme všechny možné osy — vodorovnou, svislou i obě šikmé.
Žádná osa nefunguje. Útvar 2 nemá žádnou osu souměrnosti.
Opět projdeme všechny možné osy souměrnosti.
Útvar 3 vypadá skoro souměrně, ale při žádné ose se půlky přesně nepřekryjí.
U osové souměrnosti vždy zkus všechny 4 směry osy:
- Vodorovná (vlevo-vpravo)
- Svislá (nahoru-dolů)
- Šikmá zleva nahoru doprava dolů (úhlopříčka ╲)
- Šikmá zprava nahoru doleva dolů (úhlopříčka ╱)
Děti často zapomenou na šikmé osy — a to je přesně to, co CERMAT testuje!

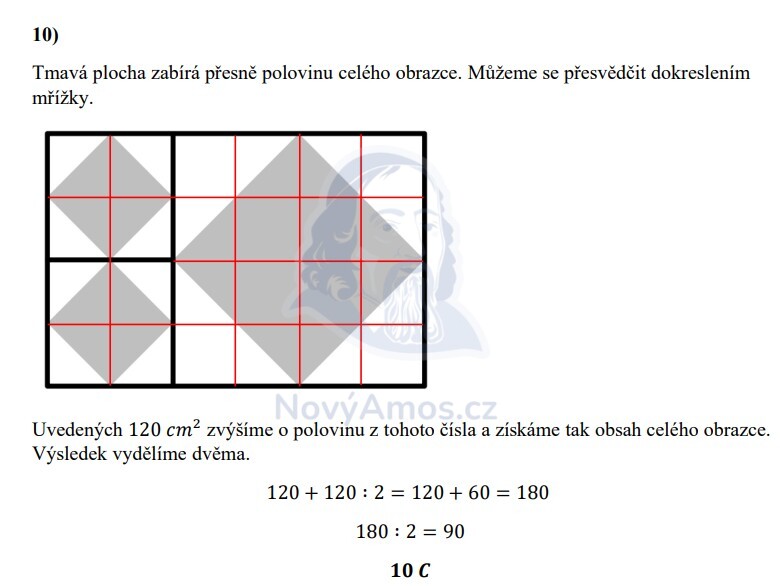
Jaký je celkový obsah všech 3 tmavých čtverců?
Možnosti: A) 60 cm² B) 75 cm² C) 90 cm² D) 105 cm² E) 120 cm²

Když do čtverce nakreslíš nový čtverec tak, že jeho vrcholy leží přesně v polovinách stran, tmavý čtverec zabírá přesně polovinu toho bílého.
·───┬───· Bílý čtverec (celý)
│ ╱ │ ╲ │ Tmavý čtverec (otočený o 45°)
├╱──┼──╲┤ = přesně POLOVINA bílého
│╲ │ ╱│
· ──┴── ·
Proč? Každý ze 4 rohových trojúhelníků je přesně čtvrtina bílého čtverce. Rohy dohromady = polovina, tmavý čtverec = druhá polovina.
Velký bílý čtverec má obsah 120 cm².
Tmavý čtverec uvnitř = polovina:
Obdélník je složen z velkého čtverce a dvou menších čtverců, které doplňují obdélník do celku. Strana malého čtverce = polovina strany velkého.
Obsah malého čtverce:
Proč dělíme 4? Strana malého čtverce je poloviční, takže obsah je 2 × 2 = 4× menší.
V každém malém bílém čtverci je tmavý čtverec = polovina:
Sečteme velký tmavý + oba malé tmavé:
Kontrola: Celý obdélník má obsah 120 + 30 + 30 = 180 cm². Tmavé čtverce zabírají přesně polovinu: 180 : 2 = 90 cm². Sedí!
Trik s otočeným čtvercem se opakuje často:
- Tmavý čtverec s vrcholy v polovinách stran = vždy polovina bílého
- Když je strana menšího čtverce poloviční, jeho obsah je 4x menší (ne 2x!)
- Celou úlohu si ověř kontrolou: součet tmavých = polovina obdélníku
Obdélník 1 obsahuje 120 mřížových bodů. Jaký je jeho obsah?
Možnosti: A) 90 cm² B) 99 cm² C) 108 cm² D) 120 cm² E) jiný výsledek

Tohle je klasický CERMAT chyták! Mnoho dětí si řekne: 120 bodů, to bude obsah 120 cm²... ale to je past!
Klíčový rozdíl:
· — · — · — · — · 4 mezery (4 cm)
1 2 3 4 5 ale 5 bodů!
Počet bodů = počet centimetrů + 1
Kratší strana: 10 bodů = 9 cm (mezi 10 body je 9 mezer).
Víme, že na kratší straně je 10 bodů. Celkový počet bodů uvnitř obdélníku (včetně okrajů) je 120.
Mřížové body v obdélníku tvoří pravidelnou tabulku — řádky krát sloupce:
12 bodů na delší straně — kolik je to centimetrů?
Mezi 12 body je 11 mezer, tedy 11 cm.
Kratší strana = 9 cm, delší strana = 11 cm:
Zapamatuj si zlaté pravidlo pro mřížové body:
- Počet bodů = počet centimetrů + 1
- 10 bodů na straně = jen 9 cm (ne 10 cm!)
- Kdyby sis to neuvědomil, dostal bys 10 × 12 = 120 — a to je přesně ta chybná odpověď D, kterou CERMAT nastražil!
- Vždy si nakresli pár bodů a spočítej mezery — jistota je jistota.

8.1) Správně upravený útvar A má právě 2 osy souměrnosti?
8.2) Správně upravený útvar B má právě 2 osy souměrnosti?
8.3) Správně upravený útvar C má právě 1 osu souměrnosti?
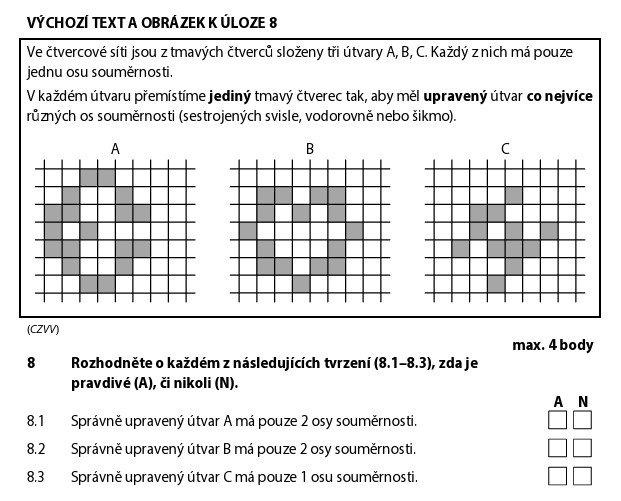
V každém útvaru máme přesunout 1 čtvereček tak, aby měl útvar co nejvíce os souměrnosti. Potom ověřujeme, jestli tvrzení o počtu os platí.
Kolik os souměrnosti může mít útvar ze čtverečků?
- 1 osa — přeložíš jedním způsobem
- 2 osy — přeložíš dvěma způsoby (např. svisle i vodorovně)
- 4 osy — přeložíš čtyřmi způsoby (jako čtverec — svisle, vodorovně i obě úhlopříčky)
Útvar A původně má 1 osu souměrnosti. Po přesunutí 1 čtverečku na správné místo získáme útvar, který má 2 osy souměrnosti (svislou a vodorovnou).
Víc os (3 nebo 4) z tohoto tvaru nedostaneme — 2 je maximum.
Po přesunutí 1 čtverečku na správné místo vznikne útvar ve tvaru znaménka plus (+). Takový útvar má 4 osy souměrnosti!
·■· 4 osy:
■■■ │ svislá
·■· ─ vodorovná
╲ úhlopříčka
╱ úhlopříčka
Tvrzení říká „právě 2 osy“ — ale útvar B má 4 osy. Takže:
Po přesunutí 1 čtverečku získáme útvar, který má 2 osy souměrnosti (svislou a vodorovnou).
Tvrzení říká „právě 1 osa“ — ale útvar C má 2 osy. Takže:
U úloh „přesuň 1 čtverec, aby měl co nejvíc os“:
- Zkus vytvořit co nejsymetričtější tvar — kříž (+) má 4 osy!
- Pozor na slovo „právě“! Pokud útvar má 4 osy a tvrzení říká 2 osy — odpověď je NE.
- Vždy si útvar nakresli a zkus ho „přeložit“ všemi 4 směry.

🎯 Rady pro CERMAT: Obsahy a souměrnost
Co si odnést z tohoto tématu
- Tmavý čtverec otočený v bílém (vrcholy v polovinách stran) = vždy přesně polovina bílého čtverce
- U souměrnosti zkus vždy všechny 4 směry osy (svislá, vodorovná, obě úhlopříčky)
- Kříž (+) z čtverečků má 4 osy souměrnosti — to je maximum pro běžné útvary
- Mřížové body: body na straně = centimetry + 1
- Mřížové body ≠ obsah! Když máš 10 bodů na straně, strana měří jen 9 cm (ne 10 cm)
- Osy souměrnosti můžou být šikmé — nezapomeň na úhlopříčné osy!
- Slovo „právě“ znamená přesně tolik — 4 osy ≠ „právě 2 osy“
- Polovina strany = obsah čtvrtinový (ne poloviční!), protože obsah = strana × strana
- Zaměnit počet mřížových bodů s délkou strany v centimetrech
- Přehlédnout šikmé osy souměrnosti — CERMAT je testuje rád
- Říct „ano, je souměrný“ jen proto, že útvar vypadá souměrně — vždy přesně ověř
- U tmavého čtverce v bílém zapomenout, že polovina strany znamená čtvrtina obsahu