Obvod B je o 4 cm menší než obvod C.
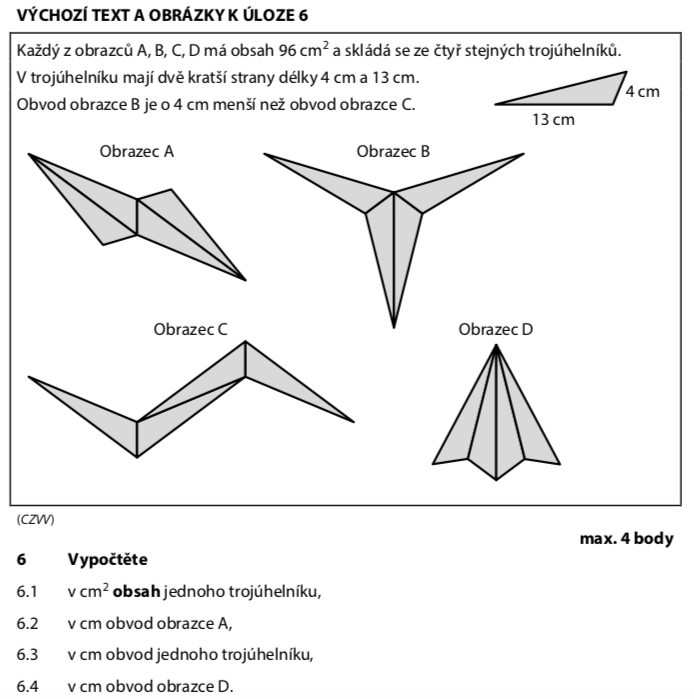
Celý obrazec má obsah 96 cm² a skládá se ze 4 stejných trojúhelníků. Stačí vydělit:
Jeden trojúhelník má obsah 24 cm².
Podíváme se na obrazec A — jeho vnější obvod tvoří jen některé strany trojúhelníků. Z obrázku vidíme, že po obvodu jdou 4 strany délky 13 cm a 2 strany délky 4 cm:
Víme, že obvod B je o 4 cm menší než obvod C. Rozdíl 4 cm vznikne právě tím, že v jednom obrazci je na obvodu třetí strana (ta nejdelší) a ve druhém není.
Porovnáním obou obrazců zjistíme, že rozdíl 4 cm odpovídá rozdílu: třetí strana mínus dvě kratší strany, které ji nahrazují. Takže:
Obvod jednoho trojúhelníku:
Obrazec D má na obvodu 2 strany délky 15 cm a 4 strany délky 4 cm:
Když máš složený obrazec ze stejných dílů, nakresli si každý tvar zvlášť a počítej jen vnější strany. Vnitřní strany (kde se trojúhelníky dotýkají) se do obvodu nepočítají!

A) méně než 320 B) 320 C) 360 D) 400 E) více než 400
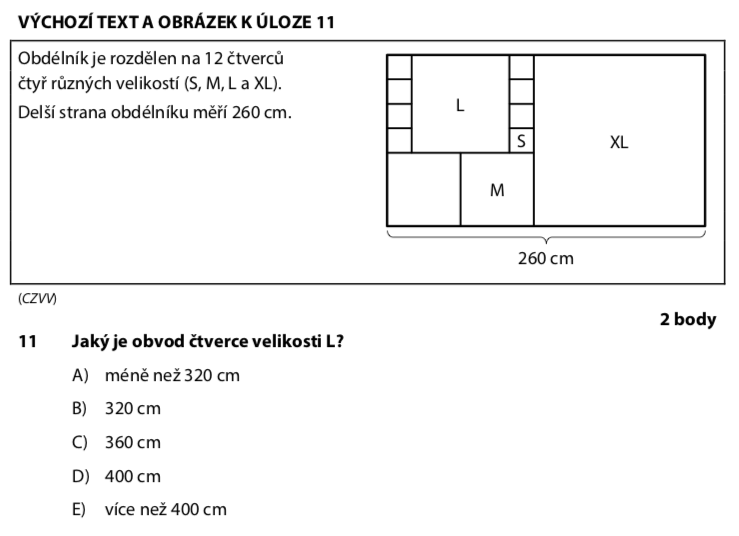
Klíč je najít, jak na sebe čtverce navazují. Z obrázku vidíme, že delší strana obdélníku se skládá ze 13 stran nejmenšího čtverce S:
Čtverec L má stranu rovnou 4 stranám čtverce S:
Obvod čtverce = 4 × strana:
U úloh s různě velkými čtverci v obdélníku: vždy hledej nejmenší čtvereček. Všechny ostatní velikosti se dá vyjádřit jako násobek toho nejmenšího. Pak stačí spočítat, kolik dílků se vejde na známou stranu.

A) 500 B) 510 C) 520 D) 530 E) jiný počet

Kratší strana má 10 bodů, ale měří jen 9 cm. Proč? Mezi 10 body je jen 9 mezer (jako ploty a slípky)!
Každá mezera je tedy 1 cm.
Obvod obdélníku = 2 × (delší + kratší). Odečteme obě kratší strany:
Delší strana = 51 cm = 51 mezer. Počet bodů je vždy o 1 víc než mezer:
Kratší strana: 10 bodů (to už víme).
Body tvoří obdélníkovou síť — počet řádků × počet sloupců:
Počet bodů ≠ délka v cm! Mezi 10 body je jen 9 mezer. Je to jako plot: 10 kůlů = 9 mezer mezi nimi. Tohle je klasická „Cermatovina" — schválně ti dá jednu informaci v bodech a druhou v centimetrech, aby tě zmátli.


Obrazec je složený ze čtverce (strana 5 cm), dvou rovnostranných trojúhelníků (taky strana 5 cm) a dvou obdélníků. Kratší strana obdélníku = 5 cm (společná se čtvercem).
Na obvodu celého obrazce jsou:
- 4 delší strany obdélníků (neznáme je)
- 6 kratších stran délky 5 cm
Obvod = 4 delších + 6 kratších = 54 cm. Nejdřív odečteme kratší strany:
To je součet 4 delších stran:
Obvod jednoho obdélníku:
Musíme spočítat všechny čtverce, které mají zakresleny všechny 4 strany. Nehledáme jen malé 1×1, ale i větší!
- Čtverce 1×1: spočítáme všechny malé čtverečky → 13
- Čtverce 2×2: hledáme větší čtverce ze 4 malých → 5
- Čtverce 3×3: ještě větší → 1
Celkem je v síti 19 čtverců se všemi 4 stranami.
Když počítáš čtverce v síti, nezapomeň na větší čtverce! CERMAT rád testuje, jestli umíš najít i čtverce 2×2, 3×3 atd. Systematicky prohledej všechny velikosti od nejmenší po největší.

🎯 Rady pro CERMAT: Obvody
Co si odnést z tohoto tématu
- Najdi nejmenší dílek — všechny strany se dá vyjádřit jako násobek základní jednotky
- Spočítej vnější strany — projdi prstem kolem celého obrazce a zapiš si délku každé strany
- Obvod obdélníku = 2 × (délka + šířka) — součet sousedních stran = obvod : 2
- U čtverců v síti hledej všechny velikosti (1×1, 2×2, 3×3...)
- Vnitřní strany se nepočítají — do obvodu patří jen strany na vnějším okraji obrazce
- Počet bodů ≠ délka — 10 mřížových bodů = jen 9 cm (mezer). Jako u plotu: 10 kůlů = 9 mezer!
- Porovnání obvodů různých obrazců — CERMAT rád dá dva podobné tvary a řekne, o kolik se liší
- Zapomenout odečíst vnitřní strany — když se dva díly dotýkají, ta společná strana není na obvodu
- Záměna bodů a mezer — u mřížových úloh vždy zkontroluj, jestli počítáš body nebo centimetry
- Zapomenout na větší čtverce v síti — 2×2, 3×3 se snadno přehlédnou
- Splést si obvod a obsah — obvod je délka cesty kolem, obsah je plocha uvnitř