Pracujeme pozpátku | CERMAT 2022

📋 Zadání — 1. řádný termín, Úloha 3 (4 body)

3.1)

Neznámé číslo je větší než 1. Když ho vynásobíme samo sebou, dostaneme číslo o 17 menší než devítinásobek čísla 9. Určete neznámé číslo.

3.2)

V každé bedýnce je 6 lahví se sirupem. Každá láhev obsahuje půl litru sirupu. Ve všech bedýnkách je celkem 321 litrů sirupu. Určete počet bedýnek.

1 🧩 Příklad 3.1 — Co je devítinásobek čísla 9?

Začneme od konce — zjistíme, jaké číslo máme dostat po vynásobení:

devítinásobek čísla 9 = 9 · 9 = 81

Výsledek násobení je o 17 menší než 81. Takže:

81 − 17 = 64

Hledáme číslo, které vynásobené samo sebou dá 64.

2 🔍 Příklad 3.1 — Jaké číslo × samo sebe = 64?

Zkusíme čísla (musí být větší než 1):

7 · 7 = 49 ❌ 8 · 8 = 64 ✅ 9 · 9 = 81 ❌

Neznámé číslo je 8! 💪

3 📦 Příklad 3.2 — Kolik litrů v jedné bedýnce?

Pracujeme pozpátku od celkových 321 litrů. Nejdřív zjistíme, kolik sirupu je v jedné bedýnce:

Jedna láhev = půl litru → 2 lahve = 1 litr.

V bedýnce je 6 lahví. Kolik je to litrů?

6 lahví : 2 = 3 litry v jedné bedýnce

4 📦 Příklad 3.2 — Kolik bedýnek?

Celkem je 321 litrů. Každá bedýnka = 3 litry. Otočíme operaci: místo × 3 použijeme : 3

321 : 3 = 107 bedýnek

Ověření: 107 bedýnek × 6 lahví = 642 lahví. 642 × 0,5 litru = 321 litrů ✅

✅ Výsledek

3.1) = 8 3.2) = 107 bedýnek

💡 Tip pro CERMAT

„Číslo vynásobené samo sebou" = číslo na druhou. Stačí znát malou násobilku: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
U bedýnek pozor na půl litru — převeď si to na celé číslo (2 lahve = 1 litr) a pak se lépe počítá.
Vždy si ověř výsledek zpětným dosazením!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 4 (4 body)

V kasičce bylo 2 800 Kč. Každý den Anna brala 30 Kč a Radka 40 Kč.

4.1) Kolikátý den se kasička vyprázdnila?

4.2) Kdy zůstalo v kasičce přesně tolik, kolik si od začátku vybrala Anna?

1 💰 Kolik berou dohromady za den?

Anna bere 30 Kč a Radka 40 Kč. Dohromady za den:

30 + 40 = 70 Kč denně

Každý den z kasičky zmizí 70 Kč.

2 📅 4.1: Kdy je kasička prázdná?

Na začátku je 2 800 Kč, každý den ubyde 70 Kč. Pracujeme pozpátku od konce — kasička je prázdná (0 Kč). Otočíme: místo − 70 použijeme : 70

2 800 : 70 = 40 dní

Kasička se vyprázdní 40. den.

3 🤔 4.2: Zbytek = Annin výběr — jak na to?

Hledáme den, kdy platí: zbytek v kasičce = kolik Anna vybrala celkem.

Po několika dnech (řekněme „den"):

Anna vybrala: 30 × den Zbytek: 2 800 − 70 × den

Potřebujeme, aby se tyto dvě hodnoty rovnaly.

4 🧮 4.2: Zkoušíme čísla

Celkem za den zmizí 70 Kč (výběr obou) + Anna si z toho bere 30 Kč. Dohromady jde o kasičku 100 Kč za den (70 z kasičky ubyde + 30 musí být v Annině výběru). Zkusme to:

2 800 : 100 = 28

Ověření po 28 dnech:

Anna vybrala: 30 × 28 = 840 Kč

Zbytek v kasičce: 2 800 − 70 × 28 = 2 800 − 1 960 = 840 Kč

840 = 840 ✅ Sedí!

✅ Výsledek

4.1) 40. den 4.2) 28. den

💡 Tip pro CERMAT

Úlohu 4.1 řeš jako jednoduché dělení: celkem : denní úbytek.
U 4.2 si zkus tabulku po dnech, pokud tě mate řešení „rovnicí". Zkus den 10, 20, 28...
⚠️ Chyták: nezaměň Annin výběr (30 × den) se zbytkem v kasičce!

📝 Oficiální řešení CERMAT

📋 Zadání — 2. řádný termín, Úloha 10 (2 body)

Tři kroužky jsou propojené operacemi (viz obrázek). Podle vzoru doplň čísla do kroužků a urči jejich součet.
A) 89 B) 100 C) 122 D) 188 E) jiný výsledek

1 🔗 Jak fungují kroužky?

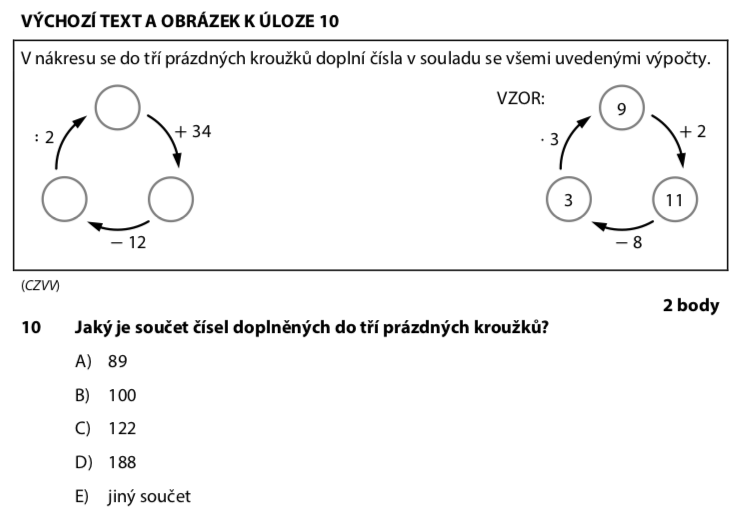
Máme tři kroužky propojené šipkami s operacemi. Musíme najít tři čísla, která splňují všechny podmínky najednou.

Z obrázku a vzorového příkladu víme, jak šipky fungují — jedno číslo s operací dá druhé číslo.

Správná čísla jsou: horní = 22, levý = 44, pravý = 56.

2 ✅ Ověření všech podmínek

Zkontrolujeme, že všechny šipky sedí:

Horní: 22 Levý: 44 Pravý: 56

Ověříme vztahy z diagramu:

44 : 2 = 22 ✅ 22 + 34 = 56 ✅ 44 + 12 = 56 ✅

Všechny podmínky splněny! 🎉

3 ➕ Součet tří čísel

22 + 44 + 56 = 122

✅ Výsledek

C) 122

💡 Tip pro CERMAT

U kroužkových úloh si nejdřív prostuduj vzor — tam vidíš, jak šipky fungují.
Zkoušej čísla systematicky. Začni od jednoho kroužku a dopočítej ostatní.
⚠️ Nezapomeň ověřit všechny šipky — i tu kontrolní!

📝 Oficiální řešení CERMAT

📋 Zadání — 1. náhradní termín, Úloha 1 (4 body)

Doplňte neznámé číslo:

1.1)

: 21 + 6 = 14

1.2)

213 : = 14, zbytek 3

1 🔙 Příklad 1.1 — Jdeme pozpátku od výsledku

Výsledek je 14. Poslední operace byla + 6. Otočíme na − 6:

14 − 6 = 8

Takže : 21 = 8. Teď otočíme dělení : 21 na násobení × 21:

8 × 21 = 168

Ověření: 168 : 21 + 6 = 8 + 6 = 14 ✅

2 🔙 Příklad 1.2 — Dělení se zbytkem

Víme: 213 : = 14, zbytek 3.

Trik: nejdřív odečteme zbytek, abychom měli dělení beze zbytku:

213 − 3 = 210

Teď platí: 210 : = 14. Otočíme : ☐ na : 14:

210 : 14 = 15

Ověření: 213 : 15 = 14, zbytek 3 (protože 15 × 14 = 210 a 213 − 210 = 3) ✅

✅ Výsledek

1.1) = 168 1.2) = 15

💡 Tip pro CERMAT

Pozpátku = otoč operaci a jdi od výsledku. Plus na mínus, násobení na dělení.
⚠️ Dělení se zbytkem: nejdřív odečti zbytek, pak teprve děl!
Vždy si ověř dosazením — dosaď číslo zpátky do původního příkladu.

📝 Oficiální řešení CERMAT

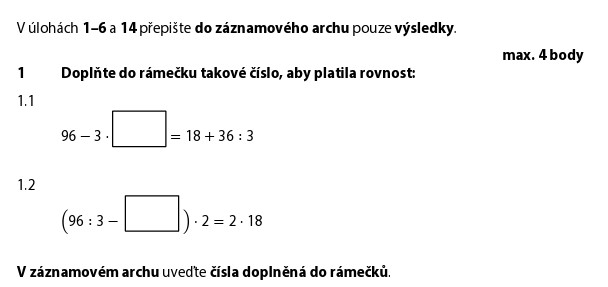
📋 Zadání — 2. náhradní termín, Úloha 1 (4 body)

Doplňte neznámé číslo:

1.1)

96 − 3 · = 18 + 36 : 3

1.2)

(96 : 3 − ) · 2 = 2 · 18

1 ➡️ Příklad 1.1 — Spočítáme pravou stranu

Začneme tím, co umíme — pravá strana neobsahuje neznámé číslo:

18 + 36 : 3 = 18 + 12 = 30

Pozor: dělení má přednost před sčítáním! Nejdřív 36 : 3 = 12, pak 18 + 12 = 30.

2 🔙 Příklad 1.1 — Pozpátku najdeme ☐

Teď víme: 96 − 3 · ☐ = 30. Pracujeme pozpátku:

96 − 3 · = 30

Kolik je 3 · ☐? Otočíme odčítání 96 − na 96 −:

3 · = 96 − 30 = 66

Teď otočíme násobení × 3 na : 3:

= 66 : 3 = 22

Ověření: 96 − 3 · 22 = 96 − 66 = 30 = 18 + 12 ✅

3 ➡️ Příklad 1.2 — Spočítáme obě strany

Pravá strana:

2 · 18 = 36

V závorce na levé straně:

96 : 3 = 32

Takže máme: (32 − ☐) · 2 = 36.

4 🔙 Příklad 1.2 — Pozpátku od výsledku

Víme: (32 − ☐) · 2 = 36. Otočíme násobení × 2 na : 2:

32 − = 36 : 2 = 18

A teď otočíme odčítání:

= 32 − 18 = 14

Ověření: (32 − 14) · 2 = 18 · 2 = 36 = 2 · 18 ✅

✅ Výsledek

1.1) = 22 1.2) = 14

💡 Tip pro CERMAT

Vždy nejdřív spočítej stranu bez ☐ — zjednoduší se ti celý příklad.
⚠️ Pozor na pořadí operací! V příkladu 1.1 se nejdřív násobí 3 · ☐ a pak odčítá od 96.
V příkladu 1.2 nezapomeň, že závorka se počítá celá dohromady — nejdřív vyřeš závorku, pak násobení.

📝 Oficiální řešení CERMAT

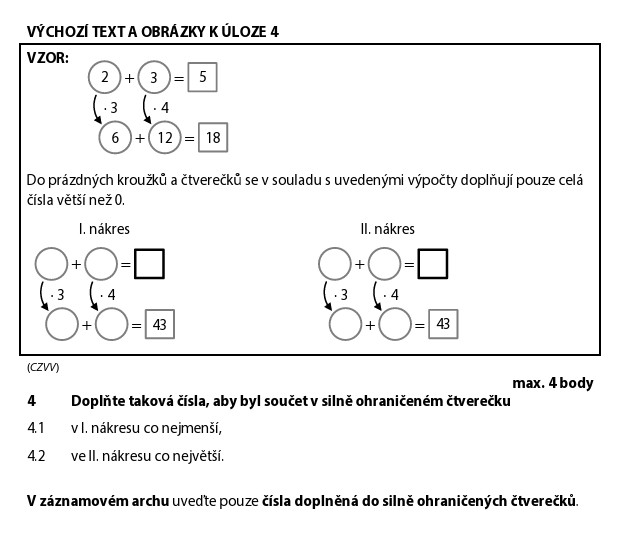
📋 Zadání — 2. náhradní termín, Úloha 4 (4 body)

Schéma: dva kroužky (čísla), jejich součet = čtvereček. Platí: levý × 3 + pravý × 4 = 43.

4.1) Jaký nejmenší součet (čtvereček) může vyjít?

4.2) Jaký největší součet (čtvereček) může vyjít?

1 🤔 Co hledáme?

Máme dvě čísla (řekněme A a B, obě jsou celá a kladná). Platí:

3 · A + 4 · B = 43

Hledáme součet A + B — jednou co nejmenší, jednou co největší.

Protože neznáme rovnice, budeme zkoušet! 💪

2 📋 Tabulka všech možností

Zkoušíme postupně hodnoty B (kolik se „vejde" do 43 při násobení 4):

B	4 · B	3 · A = 43 − 4·B	A	Součet A + B
10	40	3	1	11
7	28	15	5	12
4	16	27	9	13
1	4	39	13	14

💡 Všimni si: B může být jen 1, 4, 7, 10 — protože 43 − 4·B musí být dělitelné 3.

3 ✅ Nejmenší a největší součet

Z tabulky vidíme:

Nejmenší součet: A=1, B=10 → 11

Největší součet: A=13, B=1 → 14

Ověření nejmenšího: 3 · 1 + 4 · 10 = 3 + 40 = 43 ✅

Ověření největšího: 3 · 13 + 4 · 1 = 39 + 4 = 43 ✅

✅ Výsledek

4.1) nejmenší = 11 4.2) největší = 14

💡 Tip pro CERMAT

Když nevíš, jak na to — dělej tabulku a zkoušej! Vylučovací metoda je tvůj kamarád.
⚠️ Obě čísla musí být celá a kladná (větší než 0). Nulu nebo záporná čísla nezkoušej.
Pro nejmenší součet chceš co největší „drahé" číslo (to s větším násobkem, tady × 4). Pro největší součet naopak.

📝 Oficiální řešení CERMAT

🎯 Rady pro CERMAT: Práce pozpátku

Co si odnést z tohoto tématu

🧭 Strategie řešení

Najdi výsledek (číslo, které znáš) a od něj jdi pozpátku
Každou operaci otoč: + → −, − → +, × → :, : → ×
U složitějších příkladů nejdřív spočítej stranu bez ☐
Když nevíš, dělej tabulku a zkoušej — systematicky!
Vždy si ověř zpětným dosazením

⚠️ Typické chytáky CERMATu

Dělení se zbytkem — nejdřív odečti zbytek, pak teprve děl!
Pořadí operací — i při práci pozpátku platí: · a : mají přednost před + a −
„Číslo × samo sebe" = číslo na druhou. Nauč se řadu: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Půl litru a jiné zlomky — převeď na celá čísla (2 lahve = 1 litr)

❌ Nejčastější chyby

Otočit operaci špatným směrem — „trojnásobek" se otáčí na : 3, ne na − 3
Zapomenout na zbytek při dělení a dostat špatné číslo
V příkladu s oběma stranami (=) zapomenout nejdřív zjednodušit pravou stranu
Neověřit si výsledek zpětným dosazením — vždy projdi cestu znovu dopředu!

🔄 Pracujeme pozpátku

🔑 Pracujeme pozpátku = otočíme operaci

🎯 Rady pro CERMAT: Práce pozpátku